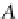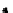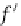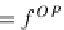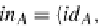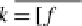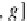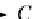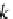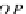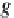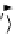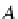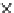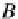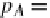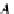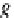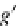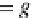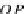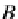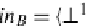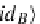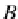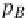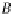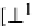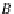Database Reference
In-Depth Information
the universal (unit) cone (a natural transformation)
η
C
:
F
. Hence, by
duality, the same functor
F
is also a right adjoint to the diagonal functor (i.e., the
adjunction,
(
Id
DB
J
−→
DB
J
) with the limit object (equal to the colimit
object above)
F(D)
and the universal (counit) cone (a natural transformation)
ε
:
F
−→
,F,η,ε)
:
DB
−→
C
and
η
=
ε
O
C
.
Let us consider, for example, the coproducts (
F
=+≡
Id
DB
J
, such that
ε
=
η
OP
) and the products
DB
J
is just
a diagram of two objects in
DB
without arrows between them (
J
is a discrete
category with two index objects 1 and 2 and with their identity arrows, so that
DB
J
(
F
=×≡+
). In this case, the diagram (a functor)
D
=
(A,B)
∈
DB
2
=
DB
×
DB
). We obtain for the universal cocone unit
η
C
(A,B)
:
(A,B)
−→
(A
+
B,A
+
B)
, one pair of the coproduct inclusion-monomorphisms
1
1
, id
B
:
η
C
(A,B)
=
(in
A
, in
B
)
where
in
A
=
id
A
,
⊥
:
A
→
A
+
B
and
in
B
=⊥
B
→
A
+
B
. Dually, for the products, the universal cone counit of the prod-
×
×
:
×
×
−→
uct
ε(A
B,A
B)
(A
B,A
B)
(A,B)
is a pair of the product
projection-epimorphisms
ε(A
×
B,A
×
B)
=
(p
A
,p
B
)
where
p
A
:
A
×
B
A
in
O
A
=[
1
and
p
B
:
A
×
B
B
. Moreover,
A
×
B
=
A
+
B
,
p
A
=
id
A
,
⊥
]
and
in
O
B
=[⊥
1
, id
B
]
p
B
=
, as represented in the following diagram:
In the case when
J
is an index category with two objects and two parallel arrows
from the first into the second object, each diagram (a functor)
D
DB
J
∈
is of the
f
g
form
B
A
. The limits of such diagrams are the equalizers, while their colim-
its are the coequalizers, as in the following example:
Example 40
Let us verify that each object in
DB
is a limit of some equalizer and
a colimit of its dual coequalizer. In fact, for any simple object
A
, a “structure map”
h
:
−→
:
→
A
is an isomorphism, thus epic and monic as well) derived from a monad
(T,η,μ)
,
where from Definition
25
, in Sect.
3.2.1
,
h
◦
η
A
=
TA
A
of a
monadic
T-algebra
(A,h)
(from Proposition
57
,
h
TA
id
A
, and
h
◦
Th
=
h
◦
μ
A
,we
obtain the
coequalizer
(by Back's theorem, it is preserved by the endofunctor
T
, i.e.,
T
creates a coequalizer) with a colimit
A
, and, by duality, we obtain the absolute
equalizer with the limit
A
as well: