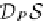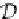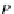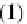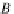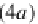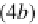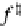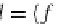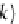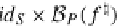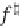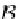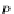Database Reference
In-Depth Information
we use the Cartesian product
×
; instead of the empty set
∅
(zero object in
Set
), the
0
singleton set
1
={⊥
}
(terminal object in
Set
); and instead of the carrier set
T
P
X
D
P
S
=
S
×
B
P
)
for the
for the initial
X
Σ
P
-algebra, we use the carrier set
gfp(
final
S
×
B
P
-coalgebra, by inverting all arrows used in diagrams for the algebras, so
that for the final coalgebra of the operational semantics we have the dual (w.r.t. the
initial algebra semantics diagrams (I1) and (I2), respectively, in Sect.
7.3.1
) com-
mutative diagrams:
0
S
={⊥
}
∅
If the set of states
which is a zero
object) and hence
f
is the constant function that maps all states into the label
'
is the singleton set
1
(dual to the
0
', with
1
Y
in
Set
, then we obtain the simpler commutative diagram
(4b) above on the right. The unique homomorphism
f
⊥
×
Y
represents the
unique coinductive extension of
k
:
Z
→
B
P
Z
along the covaluation ('renaming' of
states) function
f
:
Z
→
D
P
S
.
Let us show how the final
(S
:
Z
→
S
×
B
P
)
-coalgebra in the diagram (4a) can be reduced
to the final coalgebra semantics in the diagram (4), in the case when
Z
=
X
,
f
is
the assignment function
ass
:
X
→
S
and
k
=
℘
:
X
→
B
P
(X)
. First of all,
D
P
S
S
×
B
P
)
, and in this case
l
=
=
=[
]
is equal to the
gfp(
f,k
ass,℘
_
.Fromthe
fact that
ass
is the unique arrow from the coalgebra
[
_
]:
X
→
S
×
B
P
(X)
to the
gfp(
S
×
B
P
)
→
S
×
B
P
(gfp(
S
×
B
P
))
,
ass
is equal to
@
,
final coalgebra
B
:
[
_
]
so that the diagram (4a) is equal to the diagram (4).
7.4.1 Observational Comonad
D
P
,ε,δ
We will show that
is a cofreely generated observational comonad (dual
of the freely generated syntax monad
T
P
,η,μ
) by the behavior endofunctor
B
P
=
P
fin
(
1
Act
×
_
)
:
Set
→
Set
.
For every set
S
of states, the value
D
P
at
S
is the set
gfp(
S
×
B
P
)
of all finite
and infinite LTS trees with states in
S
and transitions in
Act
. In particular,
D
P
at the
singleton
{∗}
is the set of all finite and infinite
abstract
LTS trees where all states
are labeled by
(that is, equivalently, by states with no names).
Consequently, from the fact that the final coalgebra isomorphism
∗
B
:
D
P
S
→
S
×
B
P
(
D
P
S
)
splits into two epic projections (i.e., surjective functions)
B
=