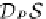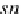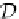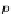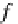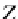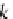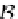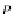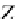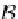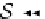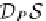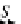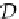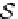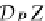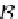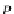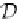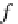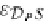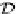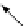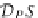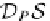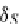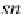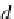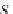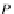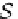Database Reference
In-Depth Information
fst
S
, snd
S
, the final coalgebra diagram (4a) above is equivalent to the following
diagram:
Hence, we obtain the endofunctor
D
P
:
Set
→
Set
, as follows:
D
P
(f )
:
D
P
Z
→
D
P
S
This function
, applied to the LTS tree
t
of the global behav-
ior, substitutes each state
s
in
t
by the 'renamed' state
f(s)
.
This coinductive principle can be used to show that the operator
D
P
inductively
extends to the
observational
comonad
D
P
:
Set
→
Set
(comonad freely generated
by behavior
B
P
), so that its coaction
D
P
f
on arrow (i.e., a function)
f
:
Z
−→
S
B
P
(
D
P
Z)
along the compos-
takes the coinductive extension of
snd
Z
:
D
P
Z
fst
Z
)
and hence the second diagram above com-
ite
f
◦
fst
Z
, i.e.,
D
P
(f )
(f
◦
mutes.
Consequently, we obtain the
observational
comonad
(
D
P
,ε,δ)
) with
ε
S
=
fst
S
,
)
while the comultiplication
δ
S
=
(id
is the unique coinductive extension of
D
P
S
snd
S
:
D
P
S
B
P
(
, and maps an LTS tree
t
into
the same tree structure (with the same transitions) where all states are substituted by
the tree
t
, as represented in the following commutative diagram:
D
P
S
)
along the identity on
D
P
S