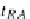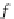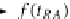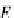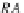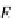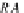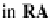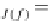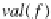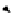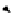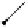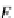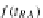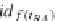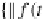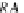Database Reference
In-Depth Information
t
RA
iff
t
RA
=
Proof
From Proposition
22
, the category
RA
is skeletal, that is,
t
RA
t
RA
,thatis,iff
t
RA
#
, and hence the iso arrows are the identity arrows.
Moreover, from the skletal property, for any two objects we have at maximum one
arrow between them. Consequently, each arrow is both monic and epic (however,
not necessarily isomorphic): it may be an isomorphism only if it is an identity (only
in this case for this pair of objects there is an inverted arrow as well).
The functor
T
e
is equal to the second comma functorial projection, intro-
duced in Sect.
1.5.1
. Thus,
RA
is an
extended symmetric
category, that is,
τ
−
1
t
RA
#
=
−→
S
nd
for the vertical composition of natural transformations
•
τ
=
ψ
:
F
st
−→
−→
T
e
and
τ
−
1
τ
=
ψ
:
F
st
=
Id
:
T
e
S
nd
. Hence, for each object
J(f)
=
t
RA
,f(t
RA
),f
in
RA
↓
RA
there is the following functorial
Eval
translation (we
recall that
ψ
J(f)
=
ψ(J(f))
=
f
) from
RA
into
DB
:
It is easy to see that the diagram on the right is just the analogous extended sym-
metric decomposition of the morphism
Eval(f )
, from the fact that
Eval
f(t
RA
)
=
f(t
RA
)
#
,
T
f(t
RA
)
#
,
⊥
⊥
=
Eval
f(t
RA
)
.
From Proposition
51
in Sect.
8.1.5
, we can show that
DB
is a monoidal category
(
DB
,
⊕
0
,α,β,γ)
, where
0
,
⊥
⊥
={⊥}
is the empty database, with the “merging”
tensor product
⊕
(in Definition
57
). The associative and idempotent properties of
⊕
is demonstrated by Proposition
51
, where
⊕
is the join operation in the com-
0
,
plete lattice
L
DB
=
(Ob
DB
,
,
⊗
,
⊕
)
with the top and bottom objects
Υ
and
⊥
respectively.
Thus, its full subcategory
DB
composed of only
simple
databases with the
top simple database
Υ
, introduced previously in Definition
26
in Sect.
3.2.5
,isa
monoidal category
(
DB
,
0
,α,β,γ)
, with a merging tensorial product
⊕
,
⊥
⊕
(equal
to the join operation of the algebraic lattice
(Ob
DB
,
,
⊗
,
⊕
)
with the top and bot-
0
, respectively; see Proposition
52
in Sect.
8.1.5
) reduced to
tom objects
Υ
and
⊥
A
B)
for any two simple databases
A
and
B
. It is easy to verify that for
any two objects (terms)
t
RA
and
t
RA
in
RA
, we have by functorial
Eval
translation:
Eval
t
RA
⊗
⊕
B
=
T(A
∪
t
RA
#
,
t
RA
=
⊥
t
RA
#
⊗
⊥
=
T
t
RA
#
,
t
RA
#
,
⊥
T
t
RA
#
⊗
t
RA
#
,