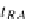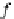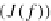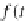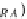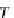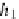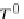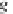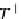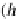Database Reference
In-Depth Information
is a
DB
morphism, where R-algebra
α
is a mapping-interpretation (Defini-
tion
11
) which satisfies this schema mapping
M
AB
, that is,
q
A,
1
∈
O(r, r, r
q
)
is operation of the expression
((
_
)
1
(
x
0
)
(
_
)(
x
0
&
x
1
)
,
v
1
∈
O(r
q
,r
)
and
α(v
1
)
is the identity function for the relational table
α(r
)
∧
(
_
)
2
(
x
1
))
⇒
=
r
ρ
α(r
q
)
#
.
Finally, the deleting of the tuples of
r
=
r
⊗
∈
A
which change the extension from
r
ρ
)
α(r)
=
r
#
into
α
1
(r)
=
o
D
(r
⊗
#
is represented in the
DB
category as
α
∗
(
α
1
(
a composed morphism
f
D
=
Eval(o
D
)
◦
h
r
:
A
)
→
A
)
.
By generalization, deleting of the tuples in
k
≥
1 different relations
r
1
,...,r
k
of a given schema
A
such that for each of them we have the mor-
phisms
h
r
i
, Eval(o
D
i
)
,
i
=
1
,...,k
can be represented in
DB
by a composed
morphism
Eval(o
D
i
)
h
r
i
α
∗
(
α
1
(
f
D
=
◦
:
A
→
A
)
),
(5.3)
1
≤
i
≤
k
1
≤
i
≤
k
,
α
1
(r
i
)
=
o
D
i
(r
⊗
r
ρ
)
#
,for
i
=
where
α(r
i
)
=
r
i
1
,...,k
, with the inter-
B
=
(
{
r
1
,...r
k
}
,
∅
)
and
α(r
i
)
=
r
i
⊗
r
i
#
,for
i
=
mediate schema
1
,...,k
,
and for each
r
A
∈
A
with
r
A
∈{
r
1
,...r
k
}
,
α
1
(r
A
)
=
α(r
A
)
.
Let us show that the functor
Eval
:
RA
→
DB
is a functor between two extended
symmetric categories:
Proposition 25
The strict monoidal category
RA
with the tensor product
⊗
(
i
.
e
.,
S
nd
,
Cartesian product _
TIMES
_
)
is an extended symmetric category with B
T
=
RA
where T
e
=
closed by the functor T
e
=
S
nd
:
(
RA
↓
RA
)
−→
B
T
ψ is the object
f(t
RA
) in
RA
,
f
component of this functor such that for any arrow f
:
t
RA
→
=
T
e
(J(f ))
S
nd
ψ(J(f))
=
=
f(t
RA
)
,
and for any arrow (h
1
;
h
2
)
:
J(f)
−→
J(g)
f in
RA
,
T
e
(h
1
;
S
nd
((h
1
;
in
RA
↓
RA
such that g
◦
h
1
=
h
2
◦
h
2
)
=
h
2
))
=
h
2
.
This is represented by
where D
h
2
(f (t
RA
))
.
All arrows in
RA
are epic and monic
.
The
associative composition operator for objects
=
g(h
1
(t
RA
))
=
∗
,
defined for any fitted pair g
◦
h
1
of
arrows
,
satisfies B
T
(g)
∗
B
T
(h
1
)
=
g
◦
h
1
=
B
T
(g
◦
h
1
)
.