Chemistry Reference
In-Depth Information
2
2
LC
−1
LC
−1
T
−1
(
V
)
2
U
T
−1
(
V
)
1
R
1
R
2
R
1
R
2
T
(
U
)
V
Z
2
Z
2
Z
0
LC
Z
0
LC
−1.5
−1.5
−2
2
−2
2
(a)
(b)
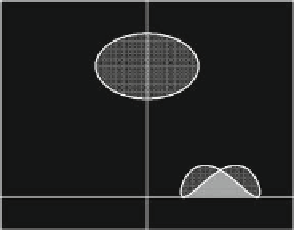
Fig. C.4
1.(
a
) The folding of the ball U
by the map along the critical line LC.(
b
) The unfolding action of the inverses of the map
A quadratic map example. Here a
D
0:3 and b
D
is the half plane Z
2
D f
.x;y/
j
y>b
g
. The line y
D
b, which separates these two
regions, is LC, that is the locus of points having two merging rank-1 preimages,
located on the line x
D
0, that represents LC
1
. Since (C.5) is a continuously
differentiable map, the points of LC
1
necessarily belong to the set of points
at which the Jacobian determinant vanishes, in other words LC
1
J
0
,where
J
0
D f
.x;y/
j
det
J
.x;y/
D
2x
D
0
g
. In this case LC
1
coincides with J
0
(the
vertical axis x
D
0) and the critical curve LC is the image of LC
1
,thatis
LC
D
T.LC
1
/
D
T.
f
x
D
0
g
/
D f
.x;y/
j
y
D
b
g
.
In order to show the folding action related to the presence of the critical lines,
we consider a plane figure (a circle) U separated by LC
1
into two portions, say
U
1
2
R
1
and U
2
2
R
2
(Fig. C.4a) and we apply the map (C.5) to the points of U .
The image T.U
1
/
\
T.U
2
/ is a non-empty set included in the region Z
kC2
,which
is the region whose points p
0
have rank-1 preimages p
1
D
T
1
.p
0
/
2
U
1
and
p
2
D
T
2
.p
0
/
2
U
2
. This means that two points p
1
2
U
1
and p
2
2
U
2
, located
at opposite sides with respect to LC
1
, are mapped in the same side with respect to
LC, in the region Z
kC2
. This is also expressed by saying that the ball U is “folded”
by T along LC on the side with more preimages (see Fig. C.4a). The same concept
can be equivalently expressed by stressing the “unfolding” action of T
1
, obtained
by the application of the two distinct inverses in Z
kC2
which merge along LC.
Indeed, if we consider a ball V
Z
kC2
; then the set of its rank
1 preimages
T
1
.V/ and T
2
.V/ is made up of two balls T
1
.V/
2
R
1
and T
2
.V/
2
R
2
.
These balls are disjoint if V
\
LC
D;
(Fig. C.4b).
Many of the considerations made above, for one-dimensional and two-
dimensional noninvertible maps, can be generalized to n-dimensional ones, even
if their visualization becomes more difficult. First of all, from the definition of crit-
ical set it is clear that the relation CS
D
T.CS
1
/ holds in any case. Moreover, the
points of CS
1
where the map is continuously differentiable are necessarily points
where the Jacobian determinant vanishes, so that





Search WWH ::

Custom Search