Oligopolies with Misspecified and Uncertain Price Functions, and Learning - Nonlinear Oligopolies: Stability and Bifurcations - page 219

1

1

x 2 x 2

P 2

E S

NE

R 2

E 2

E 1

R 1

P 1

x 1 x 1

0 1 0 1

(a) (b)

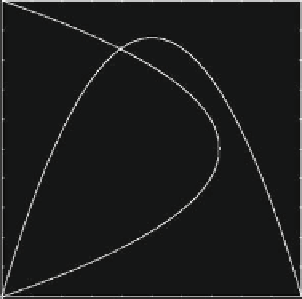
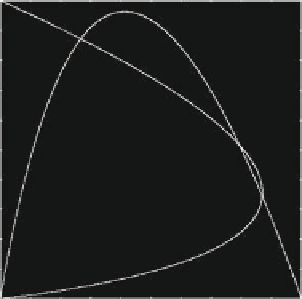
Fig. 5.1 Occurrence of multiple steady states due to misspecified demand in the duopoly game
with logistic reaction functions. ( a ) Reaction functions and the unique Nash equilibrium NE in the
full information case, " 1 D 1;" 2 D 1.( b )Now" 1 ¤ 1;" 2 ¤ 1 and multiple steady states are

obtained by overestimating the true demand

P P

These equations represent two parabolas

2 in the .x 1 ;x 2 /-plane. Both of
them pass through the origin .0;0/ and the parabola

1 and

P P

2 ) intersects the vertical
axis in the point .0;1/ (intersects the horizontal axis in the point .1;0/). So, besides
the trivial fixed point E 0 D .0;0/, we may obtain one or three positive steady states
which are located at the intersections of the two parabolas and are obtained as the
real solutions of a cubic equation. Obviously, for " k D 1 the parabola

1 (

P k coincides

with the reaction curve R k .If" k P 2

no longer coincide with the reaction curves R 1 and R 2 and intersection points do
not correspond to Nash equilibria of the “true” game, but to “subjective” equilibria
of the “perceived” game. The qualitative representation in Fig. 5.1b illustrates the
basic mechanism for the emergence of several subjective equilibria when one or
both error parameters " k are varied. In this situation there are three intersections of
the two parabolas

¤ 1 (k D 1;2), then the parabolas P 1 and

P 2 in the interior of the unit square and, consequently,
three potential long run outcomes of the game emerge (depending on their stability
properties). If, for example, both E S and E 1 are locally asymptotically stable, then
the adjustment process might guide the players to the (subjective) equilibrium E S
and, hence, close to the Nash equilibrium of the true game. However, players might
in the long run also end up in a situation represented by E 1 and, hence, far away
from the Nash equilibrium of the true game.
To illustrate these arguments, we consider the following numerical example. Let
1 D 2:8 and 2 D 2:9. For these parameter values the Nash equilibrium of the
true game is unique and globally stable for the adjustment process (5.33), which
is obtained in the full information case, with " 1 D " 2 D 1. Starting from such a
selection, if the misspecification parameter " 1 is increased, first a stable cycle of
period 2 appears (due to a saddle-node bifurcation). This is illustrated in Fig. 5.2a

P 1 and