Data Processing - Introduction to Imaging from Scattered Fields - page 60

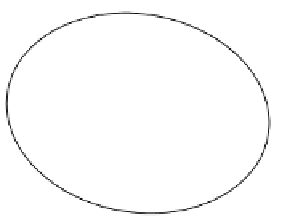
Incident
wave

Scatterer

y

Artificial
boundary

x

Figure 5.4 The general 2-D finite element scattering model.

This is the basic general equation that is used for the finite element method
in the model space that is solved iteratively along the finite element mesh. The
formation of this finite element mesh and the derivation and application of the
elemental interpolation is beyond the scope of this topic, but can be seen in
detail in Jin (2002). The bounded area is enclosed using perfectly matched lay-
ers (PML) that utilize the general relationships along the mesh on the bound-
ary of

∂
∂

ϕ
ρ

1
2

sc

� -

‚

+ jk 0 + ϕ

sc

= 0 (5.2)

ρ

∂
∂

ϕ
ρ

1 1

81

1
21

∂

2

φ

sc s c

+ jk +

ρ ρρ φ

−

sc

− (5.3)

�

( ) ( )

0

∂ϕ 2

2

( / ) + jk ρρ

2

( / ) + jk

0 0

While this method can be extremely complicated, it can be easily imple-
mented using commercially available finite element software such as
COMSOL ® to simplify this effort. This method and software packages are
used to calculate the total field at each receiver location around the target.
This greatly reduces the complexity of the approach to these types of prob-
lems, but can be computationally costly. These types of software packages
allow the user to create the target graphically, modify and/or sweep virtually
any and all parameters of interest; the program then applies the finite element
process to the model and returns both a graphical and numerical solution for
the total field in the defined space. The only challenge then is to take the out-
put and process the data into a format that can be used by imaging algorithms
developed in software packages such as MATLAB ® , which can typically be
done in a commercially available spreadsheet such as Microsoft ® Excel.
The basic COMSOL models developed and used in this text are similar
to that shown in Section 4.2. The models in this text are set up as shown in
Figure 4.1 with a fixed number of receivers equally spaced at a fixed and com-
mon distance from the target origin and a fixed number of source locations
equally spaced around the target. This can produce some very high quality
data files that can be used to test new and existing imaging algorithms as will
be shown later in this text. For the purpose of demonstrating the validity of
the data generated using this method, the imaging technique utilizing the
Ewald circles technique (Wolf, 1969) along with the Born approximation is