Data Processing - Introduction to Imaging from Scattered Fields - page 59

k y

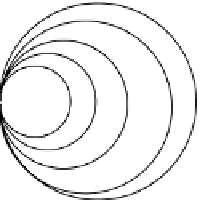
Ewald circle as a result
of using high frequency
incident plane wave

Ewald circle as a result
of using low frequency
incident plane wave

k x

Freq

Figure 5.3 The radius of these Ewald circles is specified by the magnitude of the k -vector and so changing the
incident frequency and hence, k will change the k -space data mapping as shown.

the target domain that, in theory, is only proportional to the target itself in the
weakly scattering limit, that is, in the first Born approximation.

5.2 tARget ModelIng And dAtA geneRAtIon
The task of 2-D target modeling and image data generation from scattered
fields is not a trivial one. The problem lies in that there is no general solution
for analytically determining scattered fields for an arbitrary target. There are
some analytical solutions only for a few very simple targets, but in general, no
solution exists. This means that for the varying case-by-case situations, the
analytical solution would have to be derived each time for a new target, if in
fact the analytical solution does exist at all in a closed empirical form, which
is unlikely. A common numerical solution to this type of problem or model-
ing is to use the technique of finite element analysis (Jin, 2002; Silvester and
Ferrari, 1996). In this method, the differential equations involved in calculat-
ing these scattered fields are solved numerically in an iterative process. The
basic model setup for this procedure is similar to the general model shown in
Figure 1.1, with the exception that there is an artificial boundary that defines
the extent that the iterative calculations are performed for, since this is a finite
method as shown in Figure 5.4. At this boundary the properties of the bound-
ary are defined such that there are no reflections and it gives the “appearance”
that the model space goes on forever. The general solution for an E Z polarized
field in the model space satisfies the scalar Helmholtz equation as follows:

∂
∂

1 ∂

∂

E
x

∂
∂

1 ∂

∂

E
y

� -

‚ +

� -

‚ +

(5.1)

z z

kE ε = jk ZJ

2

x µ y µ

rz 00 z

r r