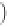Geoscience Reference
In-Depth Information
σ
, the bulk modulus of the dry porous frame
K
fr
, the bulk
modulus of the fluid
K
f
, the bulk modulus of the solid
phase
K
s
, and the shear modulus of the skeleton
G
) using
a joint inversion of seismic and seismoelectric signals. We
use a probabilistic framework to map the distribution of
errors in the observed data into the model space as a
complex error distribution. Additionally, this probabilistic
framework can easily handle the nonuniqueness of the
inverse problem, which is reflected in the probability
distribution of the model parameters.
The first criterion for joint inversion requires
that the predicted seismic and electroseismic data
fit their observed counterparts. Therefore, we perform
a Bayesian approach to estimating the following
vector,
m
, of material properties where
m
= [log
10
(
k
0
),
logit(
The objective of inverse modeling process is to update
the information on
m
, assuming a petrophysical model
or a geometrical model
M
, given data
d
and a priori
information regarding
m
. The a priori information can
come from independent observations and petrophysical
relationships. In a probabilistic framework, the inverse
problem maximizes the conditional probability of
m
in
M
occurring given the data vector
d
. We note this
probability with the statement
P
0
m
M , the a priori
probability density, or belief that the parameters of
m
in model
M
are such that the model,
M
, generates the
probability density of likelihood
P
dm
,
M
correspond-
ing to the data fit.
In a Bayesian approach, the posterior probability den-
sity
m d
of the model parameters
m
given the data
d
is obtained by using Bayes
π
ϕ
),log
10
(
σ
),
log
10
(
K
fr
),
log
10
(
K
s
),
log
10
(
K
f
),
'
formula:
log
10
(
G
)] with
logit
ϕ
= log
ϕ
1
−
ϕ
. Note that
the
md
,
M
=
P
dm
,
M P
0
m
M
P
d
M
connected porosity
is a concentration of connected
voids and is the only material property that is
constrained to be between 0 and 1; this is why we
use the logit of the function (rather than the log) to
define the associated model parameter. The logit function
is often used for linearizing sigmoid distributions of
proportions.
Another point is that we consider the set of material
properties (
k
0
,
ϕ
π
,
4 52
where
P
d
M
, the evidence, is defined as
P
d
M
=
P
0
m
M P
d m
,
M
d
m
4 53
This marginal likelihood is usually ignored because
it is not a function of the parameters
m
. For any
given model
M
, the evidence will have a constant
value. Consequently, the nature of the evidence is not
needed if we are interested only in the nature of the
variation of the a posteriori distribution rather than its
exact value.
In the following,we assume thatmodel
M
is certain (e.g.,
we know the position of the sedimentary layers and reser-
voir from seismic data andwe know that the petrophysical
model defined by Equations (4.26)
,
K
fr
,
K
f
,
K
s
, and
G
) as corresponding
to independent properties and
k
0
and
Q
V
as two
completely interrelated properties. We could also add
additional petrophysical relationships between the
poro tyonone ideandthepermeabty,the
electrical conductivity, and the bulk modulus of the
skeleton on the other side. These relationships could
be defined in a probabilistic sense, which would
improve the convergence of the inversion. However,
we prefer to stay conservative in this topic and
maintain the aforementioned properties independent
from each other.
The Bayesian solution to an inverse problem is based
on combining the information coming from geophysical
data with some a priori knowledge. In the Bayesian
approachwe use, we consider the acquisition of geophys-
ical data as experiment E. The Bayesian analysis consid-
ers both data vector,
d
, and model parameter vector,
m
,
of model
M
as random variables. Therefore, several
geometrical or petrophysical models,
M
, are possible to
explain the data. Random variables are characterized
with distributions, and we assume that all distributions
are characterized by probability density functions
(Tarantola, 2005).
ϕ
,
σ
(4.39) is exact).
Therefore, we drop the term
M
from Equations (4.52)
and (4.53). The posterior probability density
-
π
m d
of
model parameters
m
given data
d
is written as
π
m d
P
d m
P
0
m
4 54
The Bayesian solution of the inverse problem is the
whole posterior probability distribution of the material
properties. An estimate of the unknown parameters
can be computed, for example, as the expectation value
with respect to the posterior distribution (i.e., as the
mean value) or as the maximum a posteriori value which
can be understood as the most likely value.