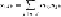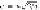Database Reference
In-Depth Information
m
ij
we generate
g
key-value pairs with value equal to
m
ij
, together with its row and column
numbers,
i
and
j
, to identify the matrix element. There is one key-value pair for each key
(
I, J, K
), where
K
can be any of the
g
groups of columns of
N
. Similarly, from element
n
jk
of
N
, if
j
belongs to group
J
and
k
to group
K
, the Map function generates
g
key-value pairs
with value consisting of
n
jk
,
j
, and
k
, and with keys (
I, J, K
) for any group
I
.
The Reduce Function
The reducer corresponding to (
I, J, K
) receives as input all the ele-
ments
m
ij
where
i
is in
I
and
j
is in
J
, and it also receives all the elements
n
jk
, where
j
is in
J
and
k
is in
K
. It computes
for all
i
in
I
and
k
in
K
.
Notice that the replication rate for the first MapReduce job is
g
, and the total commu-
nication is therefore 2
gn
2
. Also notice that each reducer gets 2
n
2
/g
2
inputs, so
q
= 2
n
2
/g
2
.
Equivalently, Thus, the total communication 2
gn
2
can be written in terms of
q
as
The second MapReduce job is simple; it sums up the
x
iJk
over all sets
J
.
The Map Function
We assume that the Map tasks execute at whatever compute nodes ex-
ecuted the Reduce tasks of the previous job. Thus, no communication is needed between
the jobs. The Map function takes as input one element
x
iJk
, which we assume the previous
reducers have left labeled with
i
and
k
so we know to what element of matrix
P
this term
contributes. One key-value pair is generated. The key is (
i, k
) and the value is
x
iJk
.
The Reduce Function
The Reduce function simply sums the values associated with key
(
i, k
) to compute the output element
P
ik
.
The communication between the Map and Reduce tasks of the second job is
gn
2
, since
there are
n
possible values of
i
,
n
possible values of
k
, and
g
possible values of the set
J
, and
each
x
iJk
is communicated only once. If we recall from our analysis of the first MapReduce
job that we can write the communication for the second job as This amount is
exactly half the communication for the first job, so the total communication for the two-
pass algorithm is Although we shall not examine this point here, it turns out that we
can do slightly better if we divide the matrices
M
and
N
not into squares but into rectangles
that are twice as long on one side as on the other. In that case, we get the slightly smaller
constant 4 in place of
and we get a two-pass algorithm with communication equal to
Now, recall that the replication rate we computed for the one-pass algorithm is 4
n
4
/q
. We
may as well assume
q
is less than
n
2
, or else we can just use a serial algorithm at one com-