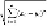Clustering - Mining of Massive Datasets - page 232

these anomalies as well. One manifestation of the “curse” is that in high dimensions, almost
all pairs of points are equally far away from one another. Another manifestation is that al-
most any two vectors are almost orthogonal. We shall explore each of these in turn.
The Distribution of Distances in a High-Dimensional Space
Let us consider a d -dimensional Euclidean space. Suppose we choose n random points in
the unit cube, i.e., points [ x 1 , x 2 , . . . , x d ], where each x i is in the range 0 to 1. If d = 1, we
are placing random points on a line of length 1. We expect that some pairs of points will
be very close, e.g., consecutive points on the line. We also expect that some points will be
very far away - those at or near opposite ends of the line. The average distance between a
pair of points is 1/3. 1
Suppose that d is very large. The Euclidean distance between two random points [ x 1 , x 2 ,
. . . , x d ] and [ y 1 , y 2 , . . . , y d ] is
Here, each x i and y i is a random variable chosen uniformly in the range 0 to 1. Since d is
large, we can expect that for some i , | x i − y i | will be close to 1. That puts a lower bound of
1 on the distance between almost any two random points. In fact, a more careful argument
can put a stronger lower bound on the distance between all but a vanishingly small fraction
of the pairs of points. However, the maximum distance between two points is and one can
argue that all but a vanishingly small fraction of the pairs do not have a distance close to
this upper limit. In fact, almost all points will have a distance close to the average distance.
If there are essentially no pairs of points that are close, it is hard to build clusters at all.
There is little justification for grouping one pair of points and not another. Of course, the
data may not be random, and there may be useful clusters, even in very high-dimensional
spaces. However, the argument about random data suggests that it will be hard to find these
clusters among so many pairs that are all at approximately the same distance.
Angles Between Vectors
Suppose again that we have three random points A , B , and C in a d -dimensional space,
where d is large. Here, we do not assume points are in the unit cube; they can be anywhere
in the space. What is angle ABC ? We may assume that A is the point [ x 1 , x 2 , . . . , x d ] and C
is the point [ y 1 , y 2 , . . . , y d ], while B is the origin. Recall from Section 3.5.4 that the cosine
of the angle ABC is the dot product of A and C divided by the product of the lengths of the
vectors A and C . That is, the cosine is