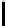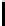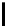Information Technology Reference
In-Depth Information
Ta b l e 2 .
Influence of the
-insensitive loss on final DSRE (
L
2
)ofUNNforproblem3D-S
h
with,
and without noise
σ
=0
.
0
σ
=5
.
0
UNN
g
UNN
g
UNN
UNN
0.2
47.432
77.440
79.137
85.609
0.4
48.192
77.440
79.302
85.609
0.6
51.807
76.338
78.719
85.609
0.8
50.958
76.338
77.238
84.422
1.0
64.074
76.427
79.486
84.258
2.0
96.026
68.371
119.642
82.054
3.0
138.491
50.642
163.752
80.511
4.0
139.168
50.642
168.898
82.144
5.0
139.168
50.642
169.024
83.209
10.0
139.168
50.642
169.024
83.209
(a) UNN,
=0
.
2
(b) UNN
g
,
=3
.
0
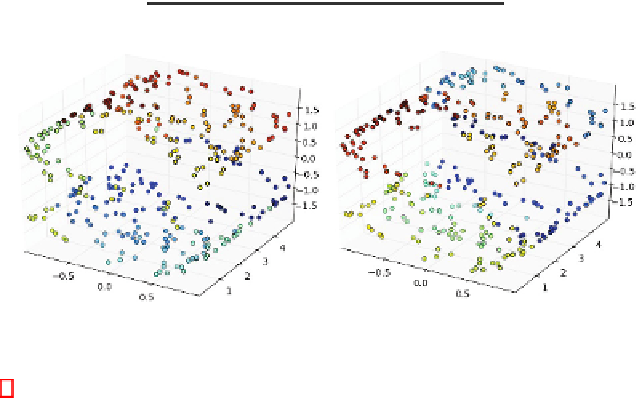
Fig. 6.
Visualization of the best UNN and UNN
g
embeddings (lowest DSRE, bold values in
Table2)of3D-S
h
without noise
seems to be slightly better than the UNN
g
embedding, blue points can again be ob-
served at different parts of the structure, representing local optima.
USPS Digits.
To demonstrate the effect of the
-insensitive loss for data spaces with
higher dimensions, we employ the USPS handwritten digits data set with
d
= 256
again
by showing the DSRE, and presenting a visualization of the embeddings. Table 3 shows
the final DSRE (w.r.t. the
L
2
-loss) after training with the
-insensitive loss with various
parameterizations for
. We used the setting
K
=10
,and
p
=10
.
0
for the Minkowski
metric. The results for digit
5
show that a minimal DSRE has been achieved for
=3
.
0
in case of UNN, and
=5
.
0
for UNN
g
(a minimum of
R
= 429
.
75561
was found for
=4
.
7
). Obviously, both methods can profit from the use of the
-insensitive loss. For
digit
7
, and UNN ignoring small residuals does not seem to improve the learning result,
while for UNN
g
=4
.
0
achieves the best embedding.