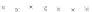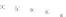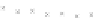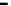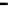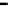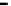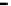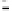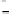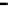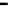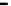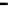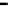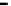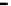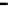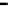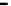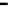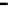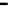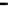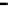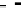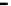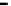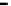SABOTAGE-TOLERANT JOB SCHEDULING FOR RELIABLE VOLUNTEER COMPUTING - Computer Science Research and Technology - page 152

255

0.02

rr1
random
ENR
ECJ(R=inf)
ECJ(R=0)
ε acc

r r 1
random
ENR
ECJ(R=inf)
ECJ(R=0)

0.018

250

0.016

245

0.014

240

0.012

0.01 235

0.008

230

0.006

225

0.004

220

0.002

0 215

0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1

c

c

(a) Error-rate (b) Computation time T

Figure 25. Error rate and Computation time for colluding rate c ( acc =0.01 , s =0.1 ,
f =0.35 , q =0.1 , p d =0 , with blacklisting)

2400

0.02

rr1
random
ENR
ECJ(R=inf)
ECJ(R=0)
ε acc

rr1
random
ENR
ECJ(R=inf)
ECJ(R=0)

2200

0.018

2000

0.016

1800

0.014

1600

0.012

1400

0.01

1200

0.008

1000

0.006

800

0.004

600

0.002

400

0 200

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

pd

pd

(a) Error-rate (b) Computation time T

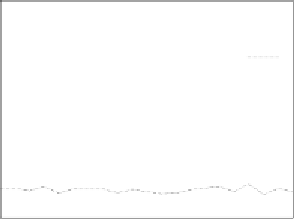
Figure 26. Error rate and Computation time for defection rate pd ( acc =0.01 , s =0.1 ,
f =0.35 , q =0.1 , P up (steady)=0.8 , with blacklisting).

In cases with blacklisting Simulation results for VC systems with blacklisting are shown

in Fig.23 - Fig.26.
Fig.23 (a) and Fig.24 (a) shows the error rates of each scheduling method as a func-
tion of sabotage rate s and fraction f , respectively. These figures show error rates of
credibility-based voting are less than acc regardless of the used scheduling method. This
means credibility-based voting can guarantee the reliability condition ≤ eacc for any s
and f regardless of the used scheduling method.
Fig.23 (b) and Fig.24 (b) shows computation times of each scheduling method. As a
function of sabotage rate s , the computation time of each method increases at first at s of
0.2, then retains almost identical values for larger s . This is true because, when s is large,
all saboteurs are caught until the end of the computation and all results produced by the