Information Technology Reference
In-Depth Information
Fig. 3.4
Semantics of probabilistic modal mu-calculus
3.6.2.1
Probabilistic Modal Mu-Calculus
Let
Var
be a countable set of variables. We define a set
L
μ
of modal formulae in
positive normal form given by the following grammar:
˕
:
=|↥|
a
ˈ
|
[
a
]
ˈ
|
˕
1
∧
˕
2
|
˕
1
∨
˕
2
|
X
|
μX.˕
|
ʽX.˕
ˈ
:
=↕
i
∈
I
p
i
·
˕
i
L
,
I
is a finite index set and
i
∈
I
p
i
=
where
a
1. Here we still write
˕
for a state
formula and
ˈ
a distribution formula. Sometimes we also use the finite conjunction
∈
i
∈
I
˕
i
and disjunction
i
∈
I
˕
i
. As usual, we have
i
∈∅
and
i
∈∅
.
The two fixed-point operators
μX
and
ʽX
bind the respective variable
X
.We
apply the usual terminology of free and bound variables in a formula and write
f v
(
˕
) for the set of free variables in
˕
.
We use
environments
, which bind free variables to sets of states, in order to give
semantics to formulae. We fix a finitary pLTS and let
S
be its state set. Let
˕
i
=
˕
i
=↥
Env
={
ˁ
|
ˁ
:
Var
ₒ
P
(
S
)
}
be the set of all environments ranged over by
ˁ
. For a set
V
ↆ
S
and a variable
X
∈
Var
, we write
ˁ
[
X
ₒ
V
] for the environment that maps
X
to
V
and
Y
to
ˁ
(
Y
)
for all
Y
X
.
The semantics of a formula
˕
can be given as the set of states satisfying it. This
entails a semantic function [[]] :
=
(
S
) defined inductively in Fig.
3.4
,
where we also apply [[]] to distribution formulae and [[
ˈ
]] is interpreted as the set of
distributions that satisfy
ˈ
. As the meaning of a closed formula
˕
does not depend
on the environment, we write [[
˕
]] f o r [[
˕
]]
ˁ
where
ˁ
is an arbitrary environment.
The semantics of probabilistic modal mu-calculus is the same as that of the modal
mu-calculus [
31
] except for the probabilistic-choice modality that is used to represent
decompositions of distributions. The characterisation of
least fixed-point formula
μX.˕
and
greatest fixed-point formula ʽX.˕
follows from the well-known Knaster-
Tarski fixed-point theorem [
52
] (cf. Theorem 2.1).
L
μ
ₒ
Env
ₒ
P
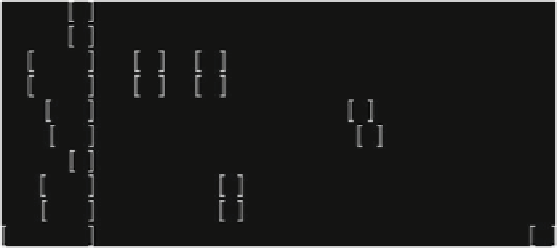






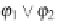

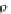

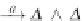






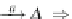


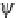



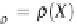



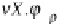
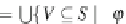


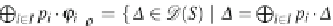

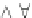
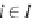

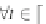





Search WWH ::

Custom Search