Game Development Reference
In-Depth Information
Converting it to our standard notation, we could rewrite the formula as
We can attribute the usefulness and popularity of the deceptively simple-looking
logistic function to the presence of that ever-so-mystical value
e
. The value
e
(also
known as Euler's number) is the base of the natural logarithm. Like the constant
pi
,
the value of
e
extends off to unfathomable lengths. For our purposes, a reasonable
approximation is 2.718281828. In fact, we can usually get away with something less
precise such as 2.718.
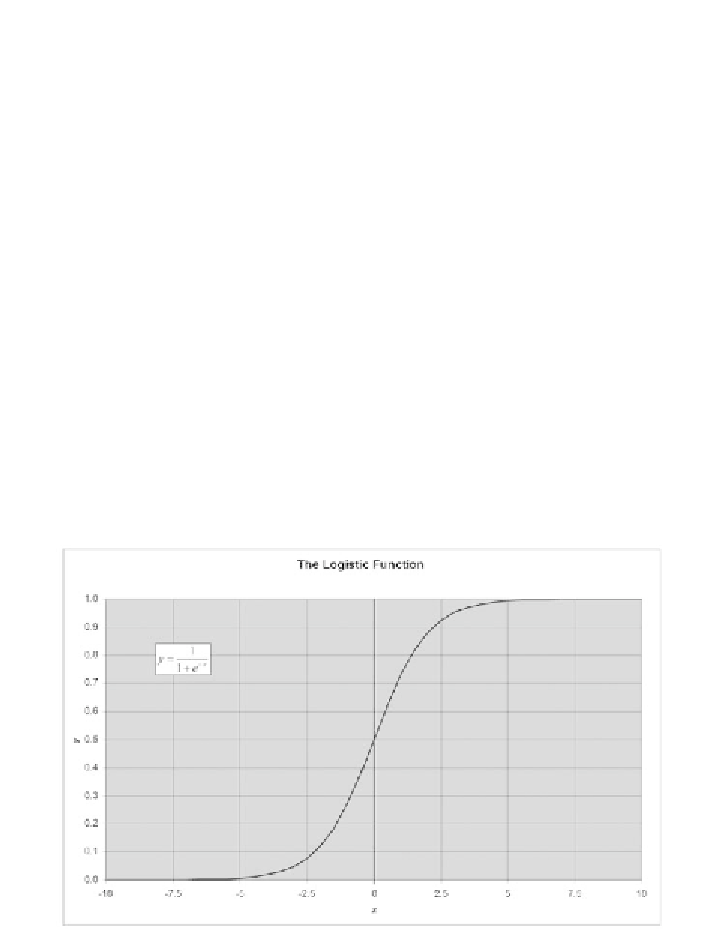
The tails of the logistic curve asymptotically approach 0 and 1 (Figure 10.7).
Given the rate at which they close, when we are using the value
e
, there really isn't
much need to calculate the logistic curve outside the
x
range of [-10...10]. At those
points, the function is within 0.0001 of the respective bounds. We can even define
cutoffs at -6 and 6, respectively, and not lose much resolution. For example, at
x
= 6,
y
= 0.9975.
If we want, we can use other, non-negative numbers besides
e
for the base in this
function. The greater the number, the narrower the shape of the logistic function.
Regardless of the base that we use, however, the values still approach the asymptotes
0 and 1.
FIGURE 10.7
The logistic function is the most commonly encountered
member of the family of sigmoid functions.