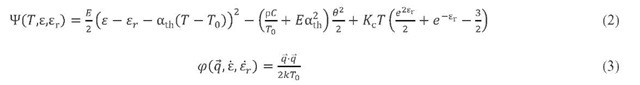ABSTRACT
Rubber-like materials can undergo very large strains in a quasi-reversible way. This remarkable behavior is often called hyper (or entropic) elasticity. However, the presence of mechanical loops during a load-unload cycle is not consistent with a purely elastic behavior modeling. Using Digital Image Correlation and Infra-Red Thermography, the present study aims at observing and quantifying dissipative and coupling effects during the deformation of natural rubber at different elongation ratios. For elongation ratios less than 2, the famous thermo-elastic inversion is revisited within the framework of the irreversible processes thermodynamics, and interpreted as a competition between two coupling mechanisms. For elongation of about 3 or 4, the predominance of entropic elasticity is shown and the relevance of the analogy with perfect gases, at the root of its definition, is energetically verified. For very large elongation ratios (about 5), the energy effects associated with stress-induced crystallization-fusion mechanisms are underlined. The current experiments, performed at relatively slow strain rate, did not exhibit any significant dissipation.
Introduction
In the literature, the first experimental studies on natural rubber were performed by Gough in the early 19th century [1]. They evidenced the coupled nature of its thermo-mechanical behavior. The experiments were resumed later by Joule [2] who observed that the straining of a vulcanized rubber generated a cooling of the specimen for small elongations, followed by a warming for higher elongations. He also noticed that the thermal expansion coefficient changes its sign – from positive to negative – with the increasing applied stress. This change of sign has since been associated with the so-called thermo-elastic inversion mechanism. This inversion phenomenon has been thoroughly studied by numerous authors (e.g. [3, 4]), and modeled within the framework of finite non-linear thermo-elasticity (e.g. [5,6]). We have recently proposed to override the hypothesis of pure thermo-elasticity to interpret this inversion phenomenon as the result of the competition between two concurrent coupling effects: a standard thermo-elastic effect (associated with the classical thermo-dilatation of materials), and a rubber effect (similar to perfect gas effect). At the micro scale, the macromolecular approach indeed highlights the very high mobility of the rubber molecular chains. Various experiments [2, 7] showed that the elasticity of this material was due to the entropy variation of the molecular chains network. They also suggested that the coupling mechanism was associated with the unfolding of the chains.
The macromolecular approach is classically integrated within the statistical thermodynamics framework, and more specifically within the kinetic theory of gases. Using this analogy, which is the basis of "entropic elasticity" or "rubber elasticity", one can demonstrate that the stress is proportional to the temperature, and that the internal energy depends only of the temperature (as a perfect gas) [4]. These results imply that the deformation energy developed by the material is totally transformed into heat [8, 9]. Numerous models were proposed in order to predict the mechanical behavior of rubber materials, but very few were able to also take possible dissipative effects (inducing self-heating) and thermo-mechanical coupling (associated with the material thermo-sensitivity) into account.
This study aims at observing, understanding and modeling the dissipative and thermo-mechanical coupling effects involved in the deformation of natural rubber during small amplitude cyclic loading around different given elongations. The material behavior analysis is achieved through energy balances performed using complementary imaging techniques, namely InfraRed Thermography (IRT) and Digital Image Correlation (DIC), giving simultaneously temperature and strain fields on the sample surface. The present paper describes the experimental procedure in a first part. The obtained results are shown and discussed in a second part. A heuristic thermo-mechanical model that account for the main characteristics of the observed energy balance is finally proposed.
Experimental setup and tests
The experimental setup is presented in Fig.1.a. It involves a testing machine and two cameras set perpendicularly to the sample surface. An infrared "Titanium" camera (Cedip) provides thermal images of the surface, while a "Camelia 8M" camera (Atmel) gives images in the visible spectrum of the sample during the test. The sample is a classical dog bone shaped specimen, as illustrated in Fig.l.b. The dimensions of the gauge part of the sample are the following: initial length L0 (35 mm), width w0 (6 mm), and thickness t0 (2.1 mm).
Fig. 1: (a) experimental setup, (b) sample geometry
The in-plane deformation is measured using a mark tracking technique. The initial gauge length between the vertical marks L0gp is 6 mm and the axial elongation is computed as the ratio of the current gauge length LGP obtained by the marks tracking algorithm and the initial one.
A specific calibration allows converting the thermal radiation digitized by the infrared camera into temperature. This calibration involves a black body with a uniform high emissivity coating, and guaranteed temperature homogeneity. As the sample undergoes very large deformations (more than 500%), it is not possible to paint or cover it in order to homogenize and increase its emissivity. Un-stretched natural rubber have a high emissivity (>0.9), and we have checked that it does not significantly change with the material elongation. The temperature variations are very small (less than 0.5 K), and it is necessary to take account of the environment thermal fluctuations that modify the heat exchanges with the surroundings.
These fluctuations are determined by placing a reference sample (of same material, and same geometry) in the immediate vicinity of the loaded sample. The thermal variations of this sample are used to estimate the thermal fluctuations of the sample environment. The heat sources, responsible for the temperature variations, are deduced from the in-plane thermal measurements, using the integrated form of the heat equation given in Eq. 1 [10]:
where wh represents the overall heat sources developed within the material, p the mass density of the material, C the specific heat, t a time constant characterizing the linearized heat exchanges by diffusion, convection, and radiation. The particular time derivative of the temperature variation 0 in (Eq. 1) is computed using the kinematic and thermal data given by the two cameras. The geometric transformation between the frames of reference of the two cameras is determined using a calibrated target. The whole experimental procedure is described in [11]. Furthermore, the "time constant" t, characterizing the overall heat losses, depends on the geometry of the sample that changes significantly during the test. A classical heat fin model allowed us to take the evolution of t with the measured axial elongation ^GP into account.
Two types of tests were performed. The first ones aimed at characterizing the thermo-elastic inversion phenomenon. The sample was submitted to a constant load (masses varying from 0 g to 730 g), and it was then heated of 25 K. Its deformation was recorded during the thermal return at room temperature. This test is the "dual" of the one performed by Anthony [12] where the stress evolution was measured at constant elongation during the temperature change. The thermal expansion coefficient can be derived by plotting strain vs. temperature. The second type of tests consists in a velocity-controlled ramp (v = 10 mm.s-1) up to a given maximum elongation (^GPM), followed by several loading cycles performed at a given elongation amplitude (A^GP) with a given loading frequency (fL). Cycles were designed to separate the coupling from the dissipative mechanisms.
Results
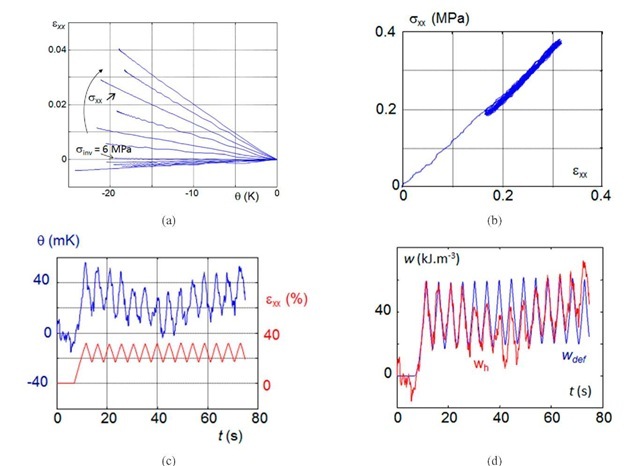
Fig.2.a illustrates the results obtained on the thermo-elastic inversion test. It represents the evolution of the axial Hencky strain exx with the temperature variation 0 – the initial temperature being higher than the room temperature – for different imposed loads (here the axial Cauchy creep stress oxx). The existence of thermo-mechanical couplings is here obvious as the material deforms when its temperature varies. We can clearly distinguish the manifestations of two opposite couplings since the material tends to contract when temperature decreases for small applied loads, and to expand for higher loads. The inversion stress oinv corresponds to the case where these opposite couplings annihilate one another.
Fig.2.b shows the mechanical response of the natural rubber during a cyclic test at
We can observe the quasi-linear response and the non-hysteretic character of the material behavior in this range of elongation. The thermal response is plotted in Fig.2.c that represents the imposed axial strain and the sample temperature with respect to time t. The temperature variations remain small throughout the test (less than 0.05 K), and the existence of a small thermal drift (amplitude smaller than 0.02 K), uncorrected by the experimental protocol described earlier can be noticed. Nevertheless, the coupled nature of the material behavior can be clearly observed as the temperature evolves in phase with the applied load.
Fig.2.d represents the time course of the deformation energy
representing the eulerian strain rate tensor -, and of the heat
The deformation energy is, in good approximation, equal to the heat during all the cycles. This experimental result confirms the existence of a thermo-mechanical coupling, and its entropic nature (i.e. similar to perfect gases). Furthermore, the amplitude of the possible dissipative effects seems to be negligible when compared with the amplitude of the thermo-mechanical coupling sources.
Fig.2: Experimental results for small elongations (X < 1.5), (a) thermo-elastic inversion test: thermal dilatation response, (b) cyclic test: mechanical response, (c) cyclic test: thermal response, (d) cyclic test: calorimetric response
Discussion
The preceding results led us to propose a heuristic constitutive model involving two competing coupling mechanism (a classical thermo-elasticity and a rubber elasticity) in series, with no intrinsic dissipation. In a simple one-dimensional approach, three state variables are chosen: the temperature T, the logarithmic strain e and a rubber strain e,., which play the role of internal state variable. The potentials defining the behavior model are the free energy ^(T,£,£r), and the dissipation potential £, £r). They are defined in Eq. 2 and Eq. 3. The free energy is the combination of a classical thermo-elastic free energy, and the free energy of an affine 1D model.
where T0 is the room temperature (here 293 K), E is the elastic modulus, ath the linear expansion coefficient, Kc a "rubber stiffness" coefficient, q the heat influx vector, and k denotes the isotropic conduction coefficient. All the coefficients are extracted from the literature (ath « 2.10-4 K-1, p « 950 kg.m-3, C« 2150 J.kg"1.K"1), except the time constant t (t « 120 s), identified on a thermal return test, E (E = 100 MPa) and K (Kc = 1110 Pa.K-1) were identified on the basis of mechanical and thermal responses, namely the previously presented cyclic test. It is important to remark that the elastic modulus given in classical material tables is not E but the equivalent stiffness of the two "elastic moduli" in series, here worth around 1 MPa. The difference in the order of magnitudes of E and Kc insures the smallness of the elastic strain compared to the rubber strain, and consequently the rapid predominance of the entropic coupling, for which the deformation energy-rate is equal to the heat sources.
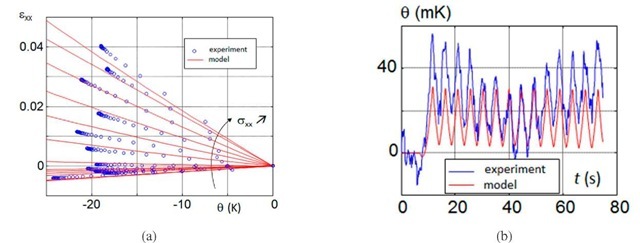
Fie.3: confrontation model/experiment (a) thermo-elastic inversion test: thermal dilatation response (b) cyclic test
The Fig.3 compares the model predictions with the experimental responses. Introducing a competition between two coupling mechanisms leads naturally to a correct prediction of the thermo-elastic inversion phenomenon by the model, as it can be seen in Fig.3.a. The thermal response of the model is also in good agreement with the experimental observations (see Fig.3.b). Naturally, the thermal noise and drift is not accounted for in the model, but the amplitude of the temperature oscillations are properly reproduced.
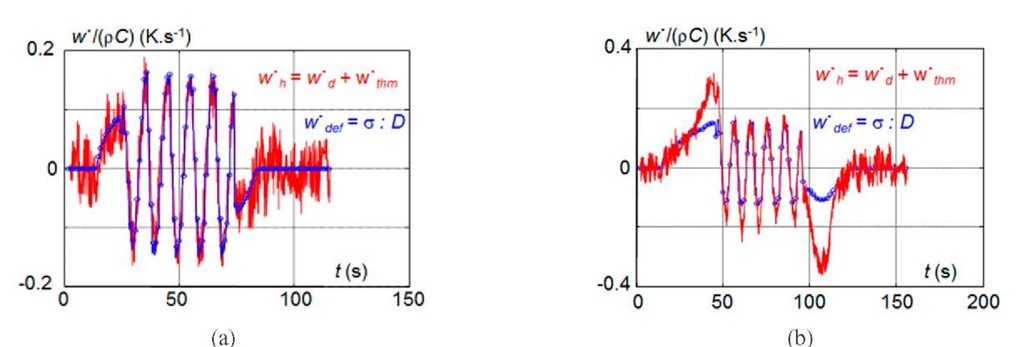
Fig.4: mechanical energy rate and heat sources evolutions during cyclic tests
at high elongations
Remember that the proposed model is quite voluntarily simple. For instance, the mechanical description of the rubber behavior can be improved by changing the form of the rubber free energy in order to obtain more realistic stress-strain responses (e.g. taking account of the limited elongation of chains). Nevertheless, we have chosen to perform other experiments in order to test the relevance of the thermodynamic hypotheses of this model in a wider range of elongations.
Fig.4 illustrates the response of the material to cyclic tests performed at a higher elongations
Fig.4.a shows that the entropic coupling remains preponderant up to elongations of 4. For higher elongations (see Fig.4.b), another coupling source appears: exothermic during the loading and endothermic during the unloading. This observation is consistent with microstructural observations of elastomers using X-ray diffraction that show the apparition-disappearance of organized phases during the loading-unloading at similar elongations. These phenomena are interpreted as crystallization-fusion mechanisms [13]. Naturally, the model should be modified to integrate the latent heat of this phase change.
Conclusion
Dilatation tests under a constant load were performed on natural rubber samples. They showed the classical effect of the thermo-elastic inversion [3,4]. Cyclic tests around different elongations highlighted the predominance of entropic effects for large elongations, the dissipative effects being negligible for the relatively small loading frequency imposed during the tests. Furthermore, the mechanical response of the natural rubber during cyclic loadings for high elongations underlined the presence of significant hysteresis loops that characterize an irreversible thermo-mechanical behavior. As a matter of fact, the interesting damping properties of this material are directly linked to the amount of energy "lost" in the loop. Let us remind that the mechanisms leading to the development of a hysteresis loop are numerous [14]. They can be entailed by: mechanical energy dissipation (e.g. viscosity effects), internal energy variations induced by microstructural evolutions within the material, thermo-mechanical couplings for non-isothermal or non-adiabatic processes (e.g. thermo-elastic effect). These latter effects seem to be predominant in the case of low frequency loadings of natural rubber.
The classical models available in the literature propose to account for the inversion effect by introducing a modified entropic elasticity [5,6] that allows to retrieve the classical thermo-elasticity for the small elongations. We propose here to leave the strict framework of elasticity and to interpret this inversion as the result of the competition between two antagonist coupling effects: a classical thermo-elasticity (induced by the thermo-dilatability of the material, since the material is not purely incompressible), and a rubber effect described by a supplementary state variable called here "rubber strain". A simplistic constitutive model, written in the framework of the generalized standard material formalism, and integrating the above-mentioned properties, was proposed. In its simple "1D" version, the model has been identified using a single cyclic test 
and values from the literature. We have checked that this model was able to predict directly the thermo-elastic inversion effect, and the preponderance of the rubber effects for large deformations
as the deformation energy was totally transformed into heat. For larger deformations
another coupling effect appeared. This effect can be correlated with stress-induced crystallization-fusion mechanisms observed in similar materials for similar elongation levels. It is noteworthy that the mechanical dissipation remained negligible for such damping materials. In order to observe the thermal effects of such material dissipation, cyclic tests are now under way at higher loading frequencies (i.e. several tens of Hertz).
