Fundamentals for Finite Element Method Part 4

Transient Response

Structural systems are very often subjected to transient excitation. A transient excitation is a highly dynamic, time-dependent force exerted on the solid or structure, such as earthquake, impact and shocks. The discrete governing equation system for such a structure is still Eq. (3.96), but it often requires a different solver from that used in eigenvalue analysis. The widely used method is the so-called direct integration method.

The direct integration method basically uses the finite difference method for time stepping to solve Eq. (3.96). There are two main types of direct integration method: implicit and explicit. Implicit methods are generally more efficient for a relatively slow phenomenon, and explicit methods are more efficient for a very fast phenomenon, such as impact and explosion. The literature on the various algorithms available to solving transient problems is vast. This section introduces the idea of time stepping used in finite difference methods, which are employed in solving transient problems.

Before discussing the equations used for the time stepping techniques, it should be mentioned that the general system equation for a structure can be re-written as

where D is the vector of velocity components, and C is the matrix of damping coefficients that are determined experimentally. The damping coefficients are often expressed as proportions of the mass and stiffness matrices, called proportional damping (e.g. Petyt, 1990; Clough and Penzien, 1975). For a proportional damping system, C can be simply determined in the form

where cK and cM are determined by experiments.

Central Difference Algorithm

We first write the system equation in the form

where Fresidual is the residual force vector, and

is defined as the internal force at time t. The acceleration, D, can be simply obtained by

In practice, the above equation does not usually require solving of the matrix equation, since lumped masses are usually used which forms a diagonal mass matrix [Petyt, 1990].

The solution to Eq. (3.110) is thus trivial, and the matrix equation is the set of independent equations for each degree of freedom i as follows:

whereis    the    residual    force,    and mi is the lumped mass corresponding to the i thDOF.

We now introduce the following finite central difference equations:

By eliminatingfrom Eqs. (3.112) and (3.114), we have

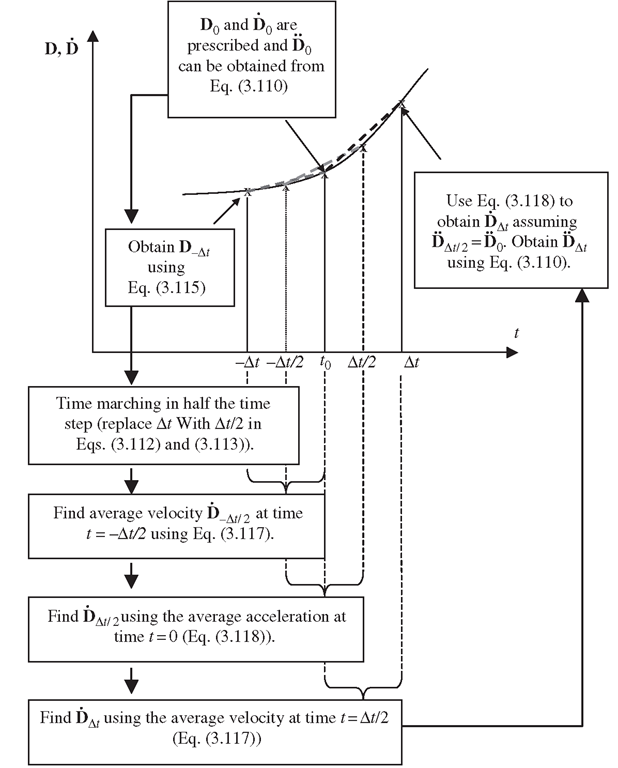
To explain the time stepping procedure, refer to Figure 3.5, which shows an arbitrary plot of either displacement or velocity against time. The time stepping/marching procedure in the central difference method starts at t = 0, and computes the acceleration D0 using Eq. (3.110):

For given initial conditions, D0 and D0 are known. Substituting D0, D0 and D0 into Eq. (3.115), we find D-At. Considering a half of the time step and using the central difference equations (3.112) and (3.113), we have

The velocity,can be obtained by Eq. (3.117)  by performing  the central differencing atand    using    values    of

After this, Eq. (3.118) is used to compute

Then, Eq. (3.117) is used once again to compute

Onceis determined, Eq. (3.118) atcan be used to obtainby assuming that the acceleration is constant over the stepwhich is the prescribed initial velocity. At the next step in time, D^t is again computed using Eq. (3.110). The above process is then repeated. The time marching is continued until it reaches the final desired time.

 

 

Figure 3.5. Time marching in the central difference algorithm: explicitly advancing in time.

Note that in the above process, the solution (displacement, velocity and acceleration) are obtained without solving any matrix form of system equation, but repeatedly using Eqs. (3.110), (3.117) and (3.118). The central difference method is therefore an explicit method. The time marching in explicit methods is therefore extremely fast, and the coding is also very straightforward. It is particularly suited for simulating highly nonlinear, large deformation, contact and extremely fast events of mechanics.

The central difference method, like most explicit methods, is conditionally stable. This means that if the time step, At, becomes too large to exceed a critical time step, Atcr, then the computed solution will become unstable and might grow without limit. The critical time step Atcr should be the time taken for the fastest stress wave in the solids/structure to cross the smallest element in the mesh. Therefore, the time steps used in the explicit methods are typically 100 to 1000 times smaller than those used with implicit methods, outlined in the next subsection. The need to use a small time step, and especially its dependence on the smallest element size, makes the explicit codes lose out to implicit codes for some of the problems, especially for those of slow time variation.

Newmark’s Method (Newmark, 1959)

Newmark’s method is the most widely used implicit algorithm.The example software used in this topic, ABAQUS, also uses the Newmark’s method as its implicit solver except that the equilibrium equation defined in Eq. (3.106) is modified with the introduction of an operator defined by Hilber, Hughes and Taylor [1978]. In this topic, we will introduce the standard Newmark’s method as follows. It is first assumed that

where β and γ are constants chosen by the analyst. Equations (3.122) and (3.123) are then substituted into the system equation (3.106) to give

If we group all the terms involvingon the left and shift the remaining terms to the right, we can write

where

and

The accelerationscan then be obtained by solving matrix system equation (3.125):

Note that the above equation involves matrix inversion, and hence it is analogous to solving a matrix equation. This makes it an implicit method.

The algorithm normally starts with a prescribed initial velocity and displacements, D0 and D0. The initial acceleration D0 can then be obtained by substituting D0 and D0 into Eq. (3.106), if D0 is not prescribed initially. Then Eq. (3.128) can be used to obtain the acceleration at the next time step, DAt. The displacements DAt and velocities DAt can then be calculated using Eqs. (3.122) and (3.123), respectively. The procedure then repeats to march forward in time until arriving at the final desired time. At each time step, the matrix system Eq. (3.125) has to be solved, which can be very time consuming, and leads to a very slow time stepping process.

Newmark’s method, like most implicit methods, is unconditionally stable if andUnconditionally stable methods are those in which the size of the time step, At, will not affect the stability of the solution, but rather it is governed by accuracy considerations. The unconditionally stable property allows the implicit algorithms to use significantly larger time steps when the external excitation is of a slow time variation.

Remarks

Summary of Shape Function Properties

The properties of the shape functions are summarized in Table 3.1.

Sufficient Requirements for FEM Shape Functions

Properties 3 and 4 are the minimum requirements for shape functions workable for the FEM. In mesh free methods,Property 3 is not a necessary condition for shape functions. Property 5 is a sufficient requirement for shape functions workable for the FEM for solid mechanics problems. It is possible for shape functions that do not possess Property 5 to produce convergent FEM solutions. In this topic, however, we generally require all the FEM shape functions to satisfy Properties 3, 4 and 5. These three requirements are called the sufficient requirements in this topic for FEM shape functions; they are the delta function property, partitions of unity, and linear field reproduction.

Recap of FEM Procedure

In finite element methods, the displacement field U is expressed by displacements at nodes using shape functions defined over elements. Once the shape functions are found, the mass matrix and force vector can be obtained using Eqs. (3.75), (3.78), (3.79) and (3.81). The stiffness matrix can also be obtained using Eq. (3.71), once the shape functions and the strain matrix have been found. Therefore, to develop FE equations for any type of structure components, all one need do is formulate the shape function N and then establish the strain matrix B. The other procedures are very much the same. Hence, in the following topics, the focus will be mainly on the derivation of the shape function and strain matrix for various types of solids and structural components.

Table 3.1. List of properties of shape functions

Item	Name	Significant
Property 1	Reproduction property and consistency	Ensures shape functions produce all the functions that can be formed using basis functions used to create the shape function. It is useful for constructing shape functions with desired accuracy and consistency in displacement field approximation.
Property 2	Shape functions are linearly independent	Ensures the shape functions have Delta function properties.
Property 3	Delta function properties	Facilitate an easy imposition of essential boundary conditions. This is a minimum requirement for shape functions workable for the FEM.
Property 4	Partitions of unity property	Ensures the shape functions to produce the rigid body movement. This is a minimum requirement for shape functions.
Property 5	Linear field reproduction	Ensures shape functions to produce the linear displacement field. This is a sufficient requirement for shape functions capable of passing the patch test, and hence that for the FEM workable for solid mechanics problems.
Lemma 1	Condition for shape functions being partitions of unity	Provides an alternative tool for checking the property of partitions of unity of shape functions.
Lemma 2	Condition for shape functions being partitions of unity	Provides an alternative tool for checking the property of partitions of unity of shape functions.
Lemma 3	Condition for shape functions being linear field reproduction	Provides an alternative tool for checking the property of linear field reproduction of shape functions.

Properties 3,4 and 5 constitute the sufficient requirement for FEM shape functions