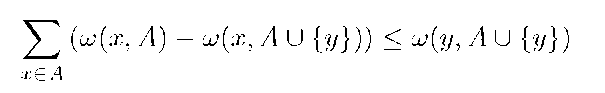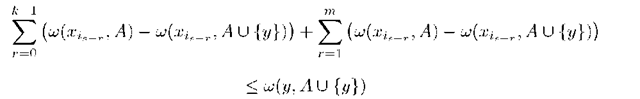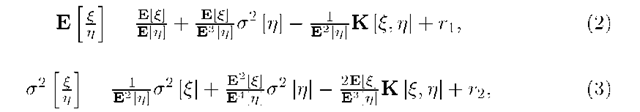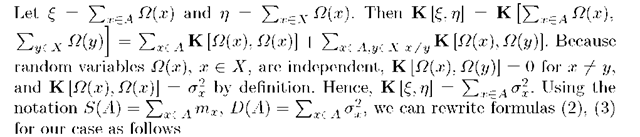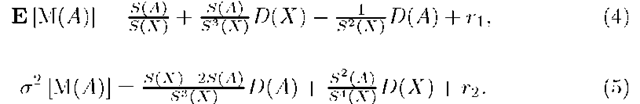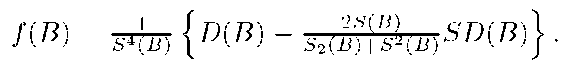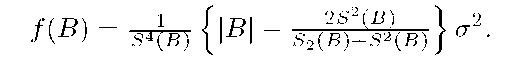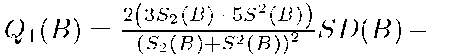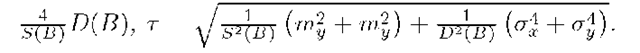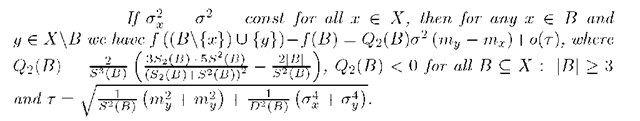Abstract
This article discusses the problem of extraction of such set of pattern features that is informative and stable with respect of stochastic noise. This is done through the stochastic information measure.
Introduction
In describing of non deterministic system we must take into account the nature of its uncertainty. In pattern recognition uncertainty could have both probabilistic nature, that defined by some additive measure, and more "imprecise" nature, which can be described, for example, by using monotonous nonadditive measures. The feature extraction is the important task of pattern recognition in general and image analyses in particular. This task consists to extraction of some minimal set of features or combinations of them from a set of features with given informativeness, which would have sufficient integral informativeness in solution of given problem of recognition. The are traditional approaches to solving this problem, such as correlation analysis (principal components analysis, etc.), discriminant analysis [2].
In this article we concretized the general problem of informative features extraction as follows. Suppose that pattern X is defined by ordered set X = 
We call every subset
a representation of pattern X. The problem is to find such representation A that it will be minimal on the one hand and it will be near to X on the other hand. Elements in the X may have different priorities, in other words, they may have different informativeness. Therefore, we will establish correspondence between the element
and the nonnegative number – a feature
, that characterize the importance of the element x for the representation of pattern X. We will determine the degree of representativeness of the set
for pattern X using the set function
and require from the set function ^ to satisfy all the axioms of monotonous measure: 1)
(monotonicity).
In addition the measure ^ meets the certain additional conditions related to the specific task of pattern recognition. We will call such measures monotonous information measures. In [1] information measures were used to set and solve the task of finding the most minimal informative polygonal representation of the curve.
In certain tasks of pattern recognition, in particular, in image processing, image analysis and image recognition random nature of image features can be caused by some noisy effects. For example, if the pattern is a discrete plane curve that extracted on the image and features are some characteristics of curve points (eg, feature is a estimation of curvature in given point of discrete curve [3]), then a random character of features (eg, curvature) is caused by the noise of image. In this case the expectation E [M(A)] characterize the level of infor-mativeness of represenation
and the variance
characterize the level of stability of representation to noise pattern. Then there is the problem of finding the most stable and informative representation
of the pattern X. The complexity of solutions of this problem will be determined by the degree of dependence of random features of each other. Stochastic measure of informativeness M will be additive measure if the features are independent random variables. Otherwise, the measure would be nonadditive measure. In this article mentioned task will be discussed and resolved in the case of probabilistic independence of random features. The case of random dependency of features is investigated in [4].
The Average Set Function of Information of Pattern
In general case the feature may be depend from all or some elements from the representation A on which it calculated i.e.
. For example, let 
be a discrete plane close curve:
and 
, where
is a point that follows from the point g in ordered representation A or
is a some estimation of curvature of plane discrete curve that is calculated in
neighbourhood of point g [3].
The degree of completeness of representation
in describing the pattern X with respect to feature
may be assigned with the follow set function
which we call averaged set function of information of pattern X (with respect to feature w). We put
if the value
is not defined for set A (in particular
Example 1. Let X = r be a discrete plane close curve:
Also we introduce the set functions
, where L(B) and S(B) are perimeter and square correspondingly of figure, that is limited by polygon with vertex in points of ordered set B. Then
and
are averaged set functions of information of curve
where
for set function
and
for set function
is a radius vector of point g G A with respect to arbitrary point O. Note that iiL is a monotonous measure, and is is a monotonous measure too if the domain bounded by polygons with vertexes in the points of discrete curve r is convex.
There is a question when the averaged set functions of information will be monotonous measure? It can be easily shown that follow proposition is true.
Proposition 1. Averaged set functions of information ^ on 2X of form (1) are a monotonous measure iff ^ obeys the following condition
and for any set
and
Corollary 1. If
for all
and .
then set function
of form (1) is an additive measure on 2X.
Let
be a some representation of pattern X. We denote
Corollary 2. Let
and
then set function
of form (1) is a monotonous measure iff
for all
and
In particular, let
for all
and
then set function
of form (1) is a monotonous measure if
for all
and
where
is a point that follows from the point x in ordered representation A.
The Stochastic Additive Average Information Measure
Let
be a averaged information measure on
of form (1) and
for all
and
In other words the feature value at point x does not depend from considered representation. The estimation of curvature
neighbourhood of point g for discrete plane curve 
is an example of this feature. Then (see corollary 1) the measure
, is an additive measure. We suppose that feature characteristics will be independence random variables
In this case the value of information measure
for fixed set
will be random variable too. The set function M(A) will be
an additive measure for any random event. We considered the example of this situation. Suppose that discrete plane curve
was subjected to additive stochastic noncorrelated noise. In result we get a random curve
where
are random noncorrelated variables and
a2[€k] = a2y k. Suppose that there is such basic set B C r for which random variables ^(g), g G B, are independent. In this case the feature characteristics w(G) = S7 (g) will be random variables just as the value of measure M(A), A G 2B, is.
Let E [f?(x)] = mx, a2 [ft(x)] = aX. We will investigate numerical characteristics of random additive measure M(A), A G 2X.
The Numerical Characteristics of Stochastic Additive Average Information Measure
Let us find the mathematical expectation of random variable M(A) with a fixed A G 2X. Random variable M(A) is equal to a quotient two random variables € = £xeA n(x) and n = Zxex n(x).
Lemma 1. Let € and n be random variables that taking values in the intervals l^, ln respectively on positive semiaxis and ln C ((1 — J)E [n], (1 + £)E [n]), l£ C (E [€] — [n] , E [€]+ ^E [n]). Then it is valid the following formulas for mean and variance of distribution of ^ respectively
where K [£, n] is a covariation of random variables € and n, could meet the certain additional conditions re i.e. K [€, n] = E [(€ — E [€]) (n — E [n])]/ ri, rx are the residuals that depend on numerical characteristics of £ and rj and \r\\ < -p^r •
Notice that, a2 [M(X\A)] = a2 [1 — M(A)] = a2 [M(A)] for A G 2X .We will use formulas (4) and (5) without their residuals. Respective values E [M(A)] = E [M(A)] — ri, a2 [M(A)] = a2 [M(A)] — r2 we will call estimations of numerical characteristics. The class of random variables {M(A) : A G 2X} satisfies all the requirements for a finitely additive stochastic measure [5]: 1) E[M2(A)] < to for all A G 2X; 2) M(A) is an almost probably finitely additive measure.
Note that mathematical expectation E [M(A)] define the set function on 2X and
Since S(A) and D (A) are additive set function then measure E [M(A)] will be additive too.
Finding of Optimal Stable Pattern Representation
We set a problem of finding such representation B of pattern X, which cardinality is less or equal to the given number
for which the summarized variance
will be minimal but the sum of squares of mathematical expectations of all representations
will be maximal. The value of summarized variance characterizes the stability of representation and all its subset to noise level of pattern and it depends also from number of elements in representation. The more elements in the presentation we have, then the summarized value of variance is greater. We will use mathematical expectations of nonnormalized information measures
, instead of 
, for simplification of computations. We introduce follow criteria:
Then it is necessary to find such set
, for which
We simplify function f (B). Let
Then it is necessary to find such set
, for which
We simplify function f (B). Let
Proposition 2. If feature characteristics of pattern X are independent random variables then following equality is true for every
Corollary 3. If
As
then following corollary is true.
Corollary 4. If
We will use the "inclusion-exclusion" procedure for finding of optimal representation which minimize the function f (B). We estimate the variation of function f (B) to the exclusion of element x from B and inclusion of element y G X\B.
Theorem 1. If feature characteristics of pattern X are independent random variables then following asymptotic equality
where is true for every
where
is true for every
Corollary 5.
Formulas from theorem 1 and corollary 5 may be use for construction of algorithmic procedures for finding of representation B, which minimize the function f. Let
The algorithm for finding of representation B of cardinality k which minimize the function f (if random variables 
are independent), consist of following steps:
1) we select the set B0 consisting of k elements of pattern X with maximal values of informativeness
as a initial representation;
2) we compute the value
from Theorem 1 and we find
argmin
, if this pair is exist. Then
is a new representation for which
accurate
within to small values of second order. This step will be repeating so long as will be pairs
If
then following conclusion follows from the corollary 5, if we disregard small values: the optimal representation B with cardinality is less or equal k, which minimize the function f will be consist of elements with the greatest values
(on the assumption of random variables
are independent).
