Shape Descriptor Based on the Volume of Transformed Image Boundary (Image Analysis)

Abstract

In this paper, we derive new shape descriptors based on a directional characterization. The main idea is to study the behavior of the shape neighborhood under family of transformations. We obtain a description invariant with respect to rotation, reflection, translation and scaling. We consider family of volume-preserving transformations. Our descriptor is based on the volume of the neighbourhood of transformed image. A well-defined metric is then proposed on the associated feature space. We show the continuity of this metric. Some results on shape retrieval are provided on Kimia 216 and part of MPEG-7 CE-Shape-1 databases to show the accuracy of the proposed shape metric.

Introduction

Shape characterization is becoming a crucial challenge in image analysis. The increasing resolution of new sensors, satellite images or scanners provides information on the object geometry which can be interpreted by shape analysis. The size of data basis also requires some efficient tools for analyzing shapes, for example in applications such as image retrieval. Reviews of proposed representations can be found in [4,5]. One class of methods consists in defining shapes descriptors based on shape signatures histogram signatures, shape invariant moments, contrast, matrices or spectral features. A shape representation is evaluated with respect to its robustness, w.r.t. noise and/or intra-class variability, compaction of the description, its invariance properties and its efficiency in terms of computation time. According to Zhang and Lu [5], the different approaches can be classified into contour-based and region-based methods, and within each class between structural and global approaches. In this paper we consider shapes as binary silhouette of objects and concentrate on global approaches. Simple global shape descriptors embed area, orientation, convexity, bending energy [6,7]. Usually, these descriptors are not sufficiently sensitive to details to provide good scores in image retrieval. Distances between shapes or surfaces have been proposed, such as the Hausdorf distance or some modification to reduce sensitivity to outlier [8,9]. In this setting, the invariance properties can be obtained by taking the minimum distance over the corresponding group of transformation. A key issue is to consider a metric for which the minimum is computed with a low computational complexity.

In this paper, we derive a 2D signature of shapes and propose a metric on the associated feature space. The first idea consists of a description of the boundary regularity by comparing the volume of the boundary neighborhood with the shape volume. The second idea is to study the behavior of this descriptor under shape transformations. We thus define a family of diffeomorphisms consisting in expanding the shape in one direction and contracting it in the orthogonal direction. In that way, for a given detail, there exists at least such a transformation enlarging its contribution to the descriptor and another one reducing it. We then derive a well defined metric on the feature space, and show its performance for shape discrimination on databases of various size.

We describe the proposed shape space and define a metric on it in Section 2. A discretization of the metric is described and evaluated on two different databases in Section 3. Finally, conclusion and perspectives are drawn in Section 4.

A Topological Description of Shapes

Shape Space

We consider shapes as 2D silhouettes of bounded objects in the image plane.

Definition 1. The pre-shape space S is the set of subsets of IR2 satisfying the following conditions:

1..is compact and connected, with a strictly positive area,

2.is connected (a has no hole).

Let us consider a shape a G S. Define the closed e-neighborhood of the set a in the sense of the Euclidean metric as where e(-, ■) is the Euclidean distance.

On this pre-shape space, we consider the Hausdorff metric (which is well-defined, see, for example, [2]) for the sets in IR2:

where

A shape space shouldembed some invariance properties. Let G be the group of transformations ofgenerated by rotations, translations, reflections and scaling :To define a shape space $ isometry- and scale- invariant, we consider:

For a givenwe notewhere vol(-)  is the area of the set.

Therefore, on the shape space S, the Hausdorff metric becomes:

where(note that this metric can be compared with the Procrustes distance for sets consisting of finite number of points [3,1]). The proof of the following proposition is not very hard and we will omit it due to the space limit.

Proposition 1. d(-, •) is a well-defined metric on S.

Volume Descriptor and Family of Transformations

The main idea of the proposed description is to characterize the behavior of shapes under some transformations. These transformations aim at enlighting small characteristic details. We first consider the volume behavior under some dilation. Intuitively, this volume will increase more for sinuous shape boundaries than for smooth shapes. Let us consider a shape a G S. Idea of our shape descriptor is based on analyzing the fraction

where vol(-) is the area of the set. This parameter is well-defined (vol(a) = 0).

We consider a family of linear transformations of IR2 in order to obtain more significant information about shapes. The goal of such transformations is to emphasize "features" of the shape in specific direction. These transformations are defined as follows:

Every where

Every

expanding in one direction (with angle 0) and ^-times contracting in orthogonal, so it is a volume-preserving transformation.

For every set

we obtain the map

For every set

It is clear that ^(a) is a continuous function of e, 0 and (3 and ig)(a) = -P(\zl ig)(a)- Note, that this function is a constant, if a is a ball (e,/3 are fixed). Let Ry be the rotation by an angle 7. We have the following property:

Property 1.

We consider Rx, the reflection with respect to x axis (horizontal line). We have the following property:

Property 2.

Let us denote R the group of transformations generated by Properties 1 and 2. The shape representation space R we consider for the fixed e > 0 is then defined by the following mapping:

expanding in one direction

 

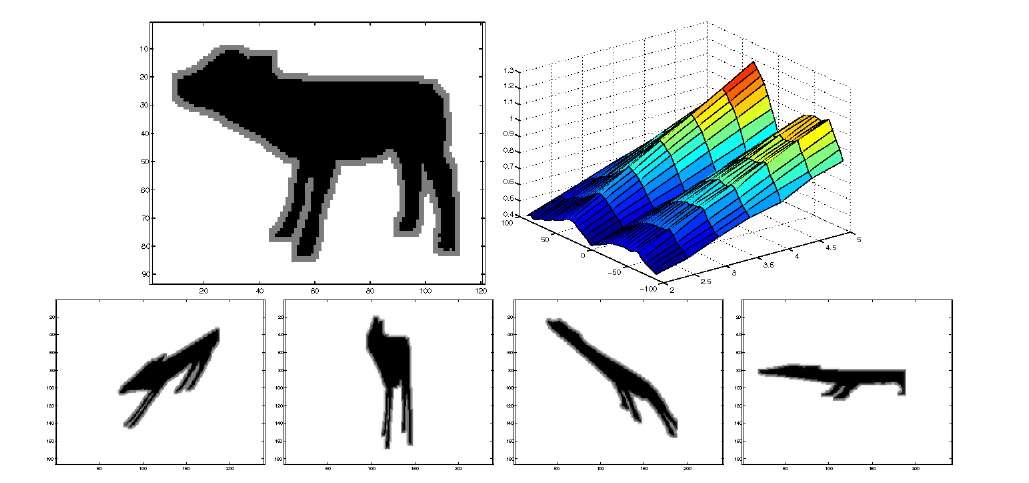
Fig. 1. Calf (top left) and the associated representationThe bottom line represents(the shape is in black and the neighborhood in grey).

 

On Figure 1, we can remark that the functionincreases more in two directions, corresponding to an extention of both the calf body and its legs.

We consider situation with no information about foreshortening and all rotations are equally likely to occur. Finally, we consider the following metric on R:

whereis a parameter,The integral on the right-hand side converges due tois almost linear function of ( for (3 big enough.

We thus have defined a map between the shape space and the feature space. Two similar shapes should be associated to close points in the feature space. This property can be established by the continuity of mapping & with respect to the metrics defined in both spaces. The proof of the following theorem we will omit.

Theorem 1.

is a continuous map.

Implementation and Results

Discretization

In practice, to compute the distance between two shapes, we have to discretize equation (7). When analysing the surfaces representing the function on Figure 1 it is clear that the embeded information is redundant. Indeed, the surfaces are very smooth, so that we can employ a drastic discretization scheme, without loosing information. We consider n = 5 pixels neighbourhood.

Before computing the proposed feature, we normalize the shapes to V = 4000 pixels (area) in order to satisfy the scale invariance.

MPEG-7 CE Shape-1 Part-B Data Set

We first evaluate the proposed approach for the 7 classes of well-known MPEG-7 CE Shape-1 Part-B data set (70 classes, each class containing 20 similar objects). Although the classes are quite distinct, this data set contains important within-class variations (see [11]).

We consider four directions,, and two expanding coefficients . The coefficient defined the metric is We consider the proposed metric between each pair of shapes (except itself of course, cause distance is 0) and report in Table 1 the percentage of correct nth neighbors for each class. The total correct answers correspond to 98% for the first neighbors. If we consider the tenth neighbors, we still obtain a total score of 85% of good retrieval. This shows the robustness of the proposed metric.

Table 1. Retrieval scores on the 7 classes of MPEG-7 database

	1st	2nd	3rd	4th	5th	6th	7th	8th	9th	10th
Bonefull	95	70	85	85	90	85	85	85	70	75
Heart	100	100	100	100	100	100	95	95	95	100
Glas	100	100	100	100	100	100	100	90	100	95
Fountain	100	100	100	100	100	100	100	100	100	100
Key	100	100	95	100	95	95	90	90	95	95
Fork	95	90	65	70	65	75	65	75	70	60
Hammerfull	95	95	80	30	30	35	30	40	35	15

Kimia Database

We considered the extended database defined by Kimia. It consists of 216 shapes divided into 18 classes (see [11]). We consider 0 g{90, 65,45, 30,0, -30, -45, -65}, and two expanding coefficients f3 G {3, 5}. The global retrieval score is 91.2% for the first neighbour, 80.1% for the second neighbour, 74.5% for the third neighbour, 72.7% for the fourth neighbour and 63% for the fifth neighbour. It shows the robustness of the proposed metric in case of a rather big database.

Our results for the first neighbour 91.2% (as well as 98% for the first database) are comparable with 98% for SC-method and 100% stated recently in [10] for Kimia 216 database. We besides have good result 80.6% for Bullseye score. It shows good localization of different classes in feature space. Our descriptor is very clear and transparent in implementation. It takes about 0.23 sec in Mat-Lab(Pentium 4, 2Gb) to find the first neighbour for one image among 215 others.

Conclusion

We have proposed a new metric on a shape space based on the shape properties after applying family of diffeomorphisms. The proposed metric is well-defined and continuous. Retrieval results on two databases, one of them consisting of 216 shapes, divided in 18 classes, have proven the relevance of this metric. Our image descriptor is invariant with respect to rotation, reflection, translation and scaling. We are currently studying the surjectivity of the associated mapping. We conjecture that surjectivity holds, at least for star shapes. Further studies (in particular 3-D shape retrieval) also include the definition of a shape classification algorithm, based on this description.