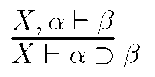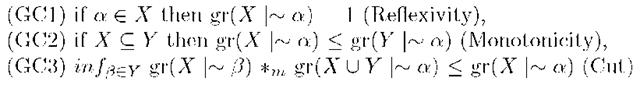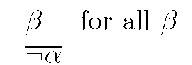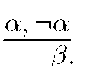Introduction, Elimination Rules for — and D: A Study from Graded Context (Pattern Recognition and Machine Learning)

Abstract

This paper is aimed to study the algebraic background of some proof theoretic rules in a set up where distinct levels of logic activity have been maintained carefully. In this regard, Introduction, Elimination rules for -i, and D have been considered as specific cases whose necessary and sufficient conditions from the perspective of graded consequence will reveal a new analysis.

Keywords: Graded consequence, Object level algebra, Meta level algebra, Introduction and Elimination rules, Proof theory.

Introduction

Natural deduction system was introduced [5] to bring into notice the prototypes of human reasoning in the form of some rules of inference. Sentences (wffs) i.e. elements of F, the set of all wffs are object level entities; whereas, the notion of inference is a meta level concept. Rules of inference lie at meta meta level to talk about the interrelation between two or more than two inferences. This distinction between levels is generally missing in the existing approaches. Gentzen’s own interpretation toIntroduction [5] is a clear evidence of mixing up meta level implication namely ‘provability’ with object level implication ‘follows’. Later on, when Sequent calculus was introduced [5], a sequent viz., is assumed to represent the truth of the object level sentence

In [7], it has been clearly mentioned that in LJ and LK (the sequent calculus presentations for Intuitionistic logic and Classical logic respectively) the presence of contraction left, weakening left, cut, &-left and &-right jointly claim the propositionif and only if

This indicates that usual practice in LJ and LK is to see meta level symbol ‘,’ and object level conjunction ‘&’ equivalently. Apart from LJ, LK, it has been a convenient practice in many other logical systems [6] also. In substructural logics [7] where some of the structural rules remain absent, the rules for & are modified in such a way that in absence of any one of the above mentioned structural rules if and only ifremains unaltered. Thus in all these approaches a lack of clarity in distinction between levels of logic activity is envisaged.

Theory of graded consequence which was introduced by Chakraborty [1] in order to generalize two-valued notion of consequence relation in many-valued context, throws light on this issue. Suppose L is a set of truth values assigned  to the sentences of F endowed with some operators, say,in correspondence to each connectiveof the object language. Now with respect toa set of fuzzy subsets any formula a gets a truth value in L. Thus determines the value of the meta-linguistic sentence ‘X semantically entails a’ or in symbolIn two-valued context,i.e. ‘for all Tj, if thenwhere eachis identified with the valuation under which all formulae of T get the value 1, involves a meta-level ‘if-then’ and quantifier ‘for all’. So, a complete lattice along with an implication ^m is needed for meta level algebra.

Now, let us consider the following form of Deduction Theorem (D-Introduction).

where X is a set of formulas andare single formulas. In algebraic term this can be restated as – ‘truth valuetruth valueOr more formally abbreviating ‘grade’ by ‘gr’ one can write –

So, to obtain Deduction Theorem (DT) as a rule of inference demands should be made to thein such a way that as a result (A) gets satisfied.

This clarifies that the algebras of different levels of logic give rise to different rules of inference. Having this as the main theme of the paper, in Section 2, the basic concept of the notion of graded consequence will be introduced and then as a specific case of study the necessary and sufficient conditions for graded Introduction, Elimination rules for D and — will be discussed. In Section 3 we will try to show that this study of proof theoretic results from the perspective of graded consequence gives a different analysis in comparison to the existing approaches.

In the Context of Graded Consequence

In graded context depending on a collection of fuzzy setsover well-formed formulas the sentence ‘a is a consequence of X’ may get values other than the top (1) and least (0). That is, the notion of derivation of a formula from a set of formulae is in general a graded concept. Usually logics dealing with uncertainties do not feel the necessity to address many-valuedness in the concept of derivation. In this regard, an overlapping standpoint with ours can be found in [6] in the concept of degree of soundness of a rule. A graded consequence relation [3] is assumed to be a fuzzy relation satisfying the following conditions.

Given a context i.e a collectionof fuzzy subsets over formulae and a meta-level algebra, consisting of operators for meta-level implication and conjunction, a sentence ‘a is a consequence of X’ gets a truth value, denoted byin L. In two-valued context, Shoesmith and Smiley [8], generalized the definition of semantic consequence with respect to a set of valuationsAccording to this definitionbasically means’for all T in

if for allGeneralizing this idea in graded context the value ofis calculated by the

In [2], it had been proved that given a contextand a complete residuated latticefor meta level algebra,is a graded consequence relation. On the other hand, it also had been proved [2] that given any graded consequence relationthere existsa collection of fuzzy subsets over formulas, such that the fuzzy relation ‘coincides withThese two results together constitutes the representation theorem. Now let us come to the context of graded rule DT i.e.

Theorem 1. A necessary and sufficient condition for graded introduction rule)

For anydefined over a complete residuated lattice L, a necessary and sufficient condition foris that for any

Theorem 2. A necessary condition for graded MP

For anydefined over a complete residuated lattice L, the necessary condition for

Theorem 3. A sufficient condition for graded MP

defined over a complete residuated lattice L, satisfy the conditions viz., for any

From this study on the necessary and sufficient condition of the graded rule DT and MP we can see that an interrelation between the two levels of implication is needed for the viability of the rules. In two valued context (both classical and intuitionistic)are the same. Also for

holds. So, both DT and MP are valid in classical as well as intuitionistic cases. As a non-trivial example, let us consider [0, 1] endowed with Godel adjoint pair as the meta-level algebra for and Lukasiweciz implication for computingThen these structures for object and meta level satisfy

and hence DT holds in this case. On the other hand, with Godel algebra as meta structure and computingby Godel implication, one can find a model for graded rule MP.

Let us now consider the rule -Introduction viz., [a]

This presentation is due to Gentzen [5]. In a language where A, the falsum constant is not present the above form is equivalent to [a]

As in this present study we are considering sequents of the form, the

respective translation will be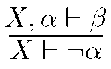for all

 

Theorem 4. A necessary condition for graded —-Introduction

For any, defined over a complete residuated lattice L, the necessary condition

for inis that

Theorem 5. A sufficient condition for graded —-Introduction

Let, defined over a complete residuated lattice L, satisfy the conditions viz.,

(i) there is an elementsuch thatfor any

(ii) for anyimplies Then inholds.

—-Elimination presented in [5] is of the form

In graded context —-Elimination is generalized as – ‘There is somesuch that inThe necessary and sufficient conditions for graded —-Elimination are as follows.

Theorem 6. A necessary condition for graded —-Elimination For any arbitrarily chosen complete residuated lattice L if graded —-Elimination holds for anythen for any non-zerothere exists some non-zero z in L such that

Theorem 7. A sufficient condition for graded —-Elimination

Letbe a complete residuated lattice determining a graded consequence relationbe the operator for object language negation — with the conditions – (i) there is some, such thatfor any b in L andthen there existssuch that

Then graded —-Elimination holds.

In two-valued contextis always 0 and hence —-Elimination holds for k

= 1. Also, the conditions suffice to have —-Introduction are true in two-valued context and hence we get —-Introduction in two-valued case. To have a non-trivial example let us considerwith Lukasiewicz adjoint pair at meta level algebra. — is defined byfor a =1 and 1 otherwise. Then for

c =1/2 one can verify the sufficient conditions for graded —-Introduction. The same structure also suffices to have graded —-Elimination; but in this case value of k will be 1. On the other hand, instead of the above definition of —o if we considerthen the value of k will be 1/2.

3 An Analysis of Proof Theoretic Rules of Inference: Existing Approaches versus the Theory of Graded Consequence

In the introduction, it has already been discussed that the existing approaches of looking at the notion of inference are so designed that the distinction between object level and meta level connectives gets mingled up. DT states impliesBut this turns out to beimplies due to the equivalent treatment given to ‘,’ and ‘&’. On the other hand, [7] along with reflexivity and cut gives rise toimplies

The algebraic counterpart ofif and only ifis given by

residuation in object level operatorsIn

this regard, the study of the background of DT from the perspective of graded consequence reveals a different analysis. In graded context, the summary of the semantic background of DT is – (i) the notion of consequencedepends on a meta-linguistic residuation pairand (ii) the object levelcomputing

This seems more close to the understanding of the rule viz.,

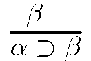
as the rule asserts an object level implication viz.,providedis provable from a’.

In Section 2, we have discussed the necessary and sufficient condition for graded —-Introduction. The necessary condition for graded —-Introduction is On the other hand, the sufficient condition demands for somewhich in two-valued scenario will reduce to

In algebraic term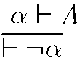, the special case of —-Introduction can be translated as

where algebraic interpretation ofand the bold line between the upper and lower sequents are represented byrespectively.

Then algebraic translation ofwould bewould be

.This translation of —- Introduction becomes transparent due to the study of graded consequence.

Conclusion

Logic generally consists of three distinct levels viz, object, meta and meta-meta level. Each of these levels has a set of vocabulary which need not be the same. So, one can think of to have different algebraic structures for different levels of language, in general. Existing approaches have not paid much attention to this. As a result, the prevalent understanding for proof theoretic rules lacks a certain degree of clarity in maintaining the distinction of levels. In this paper we tried to provide an alternative analysis taking care of the distinction between levels. In this connection, exploring an alternative semantic background for classical and intuitionistic logic from the perspective of graded proof theoretic rules can be a new direction of study.