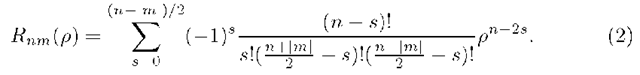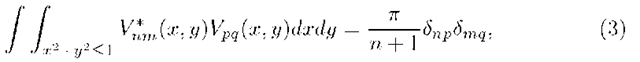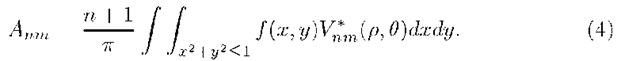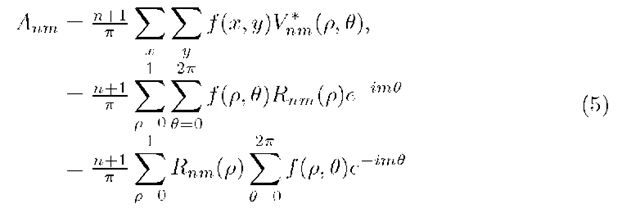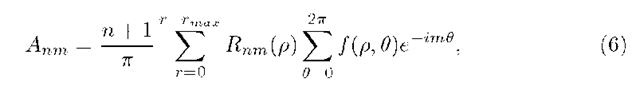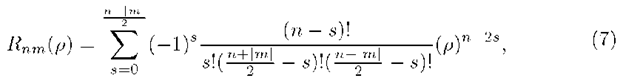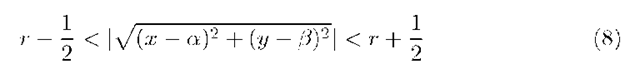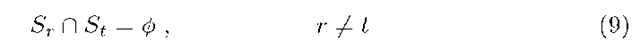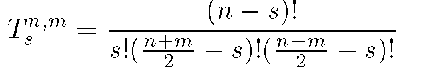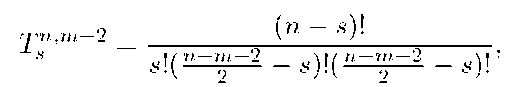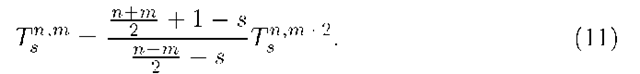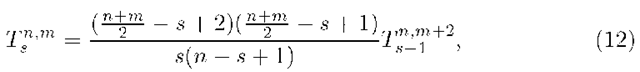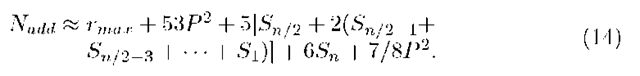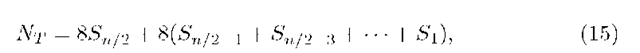Abstract
Zernike moments are found to have potentials in pattern recognition, image analysis, image processing and in computer vision, apart from its traditional field of optics. Their invariance and orthogonality are attractive in many applications. However, the study of its computational structure can lead to some efficient and fast algorithms. In this paper, we have examined the use of a discrete circular map to compute Zernike moments in polar coordinates. It should be noted that such a discrete circular map, to represent a garylevel image in polar coordinates, does not require any special kind of sampling. Hence, zernike moments in polar coordinates can be computed easily. Comparison shows the proposed method is also efficient in computation.
Introduction
Moments based on the theory of orthogonal polynomials can be used in a number of applications, namely in image analysis, image processing and pattern recognition. Teague [1] suggested to recover image from orthogonal moments using Zernike moments. An example of other orthogonal moments is based on Legen-dre polynomial. Teh et al. [2] made a study on the evaluation of various types of moments and their properties. Some other authors [3,4] examined Zernike moments and implemented that in the area of image analysis. Unfortunately, adequate attention has not been paid for the efficient computation of Zernike moments, though attempts are already made to speed up the calculation through geometric moments [6]-[11]. Mukundan and Ramakrishnan in [8] used a recursive algorithm to compute Zernike and Legendre moments. Their method takes a large number of computing operations [12]. J. Gu et al. [12] has used an iterative algorithm for the fast computation of Zernike moments. He used one dimensional FFT when the radius is a power of two and took help of Chan et al.’s algorithm [10] to compute a recursion. Yongqing Xin et al. [13] has revealed an interesting as well as very important fact about Zernike moments. They have shown that the polar Zernike moments outperform the Cartesian Zernike moments in terms of rotational invariance property. Wee et al. [14] has computed Zernike moments in polar coordinates through a traditional circle mapping technique.
In this paper, we have proposed an algorithm to compute Zernike moments in a completely different way. To compute Zernike moments, we consider discrete circular mapping [5] to map a gray-level image onto a discrete circular disc. The mapping is different from that of Wee et al. [14]. The symmetry property of the discrete circle drastically reduces the computation for moments. Rotational invariance is also found to be in line with that in [13].
Zernike Polynomials and Zernike Moments
Zernike provided a set of complex polynomials, known as Zernike polynomials, that form a complete orthogonal set on the unit disc, i.e., over the interior of the unit circle
and are described by
where n is a non-negative integer and m is an integer, subject to the condition 
is even and
is a vector from the origin of the disc to a point on it. 0 is the angle that the vector p makes with the positive direction of x-axis in the counter clockwise direction. Rnm(p) are the Zernike radial polynomials in (p, 0) polar co-ordinates and are defined by
It is easy to note that
Polynomials in equation(2) are orthogonal and therefore, we must have according to orthogonality condition
where
when
and zero otherwise.
is the Kronecker delta.
Similarly. ~
is also the Kronecker delta.
With the Zernike polynomials described above, we are now in a position to define Zernike moments corresponding to some continuous function f (x, y). Zernike moment for order n and repetition m is given by
Obviously, Zernike moment outside the unit disc is zero. If f (x,y) is a digital image, we replace the integral by summation to get Zernike moments for the image. Then Anm in this case reduces to
where,
Note that we have taken a unit circle or a unit disc is as
in the discrete plane [5] and not normally defined .
in the continuous plane.
is the image pixel value on a unit discrete circle of radius vector p. When the image is mapped on a unit discrete disc, we get the image pixels mapped on different discrete circles that define the disc. We can take
where
Thus, p = 0 when r = 0 and p = 1 when
depends on the size of the image under test. For a P x P image,
As r rotates from zero to
there is as such no way to find uniquely the correspondence between
and the image pixel. This problem also has not been addressed before. To solve this problem we have taken help of a mathematical definition of discrete circles, rings and discrete discs [5]. Below, we review, in brief, the definitions and their properties; error behavior and their generation algorithm, as they play a very significant role in the computation of Zernike moments. Thus, finally we get,
where
where
and r = 0,1, 2, • • • rmax. Since to compute the Zernike moments we need to map the graylevel image onto a discrete disc, we examine the definitions and properties of discrete circle, ring and disc in the following.
Discrete Circle, Ring, Disc and Their Properties
Discrete circle (dc):
A dc is a discrete space approximation to the circle defined in Euclidean geometry. In the present scheme of generation, a dc is defined as follows
Definition 1. A dc with radius r and center
is a set ,
of 8-connected pels so that each pel (x, y) satisfies the inequality
Proposition 1. For concentric Sr and St
Proposition 2. There cannot exist any gap or hole between any two concentric dcs of radii r and r+1.
Rings and Discs
Definition 2. A discrete ring (dr) with integer radius
and integer center
is given by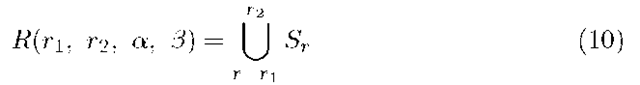 
if r\ = 0 a discrete disc (dd) is generated. Here S0 is assumed to be the center pel itself.
For the complete generation of a discrete circle, ring and disc, one can see the article [5].
Proposed Algorithm for Computation of Zernike Moments
For a particular order n we propose to compute the radial polynomial Rnm(p) (equation(2)) not term by term but in a batch. We propose two recursive relations which can be obtained in a straightforward way from the following considerations. We have,
and
where
is the term within the summation in the radial polynomial, apart from two multiplicative factors, corresponding to the summation index s, running from s = 0 to
We shall show later on how to handle these two multiplicative factors. After algebraic manipulation, one can get
Similarly, it is easy to deduce
Now, for a particular value of s, say s = 0, we use equation(11) to compute all the To terms for different values of n and m. Note that we always have,
We use equation(12) when we change the index in the term, say from T0 to Ti. It is important to note in this context that the denominator of equation (11) is infinite when
but we never encounter this situation because under such a condition, the term is computed either using the equation (12) or in terms of the previously computed value. Thus, when all the To terms are known, we compute the first term in T1 in the next step, starting with the maximum value of m, i.e., m = n — 2, the same value of m we started with to compute the first To term using equation (11).
Computational Analysis
For a P x Pimage,total number of multiplications can be shown to be
and the total number of additions as,
where,
Comparison
Below we present a comparison computational analysis of three other different methods, on an image of size P x P and maximum order of Zernike moments M. Comparison shows that in the proposed method, number of multiplications drastically reduces and is minimum of all the cases. For additions, the number also reduces very significantly, except for the method described in [9] by Belkasim et al. Our method takes a slightly more number of additions than that of Belkasim et al. (approximately 1.38 times more) but it takes approximately 11.25 times less number of multiplications than their method. This shows the effectiveness of the proposed method. It is obvious the Zernike moments are scale invariant. As computations depend on the size (P) of the image it takes care the computation of scales.
Table 1. Comparison of multiplications and additions of different methods
Conclusion
Recently Zernike moments are gaining popularity in applications of pattern recognition, image analysis and image processing but direct computation of factorials in them is time consuming and discouraging. A faster algorithm is therefore necessary and its need is already felt to various research communities. We have presented an efficient algorithm that computes the Zernike moments in a nice way. The comparison shows our algorithm is faster than the existing algorithms. Also the mapping of pixels through discrete circles, maintains the rotational invariance. The mapping is unique and leaves no holes or gaps on a disc.
