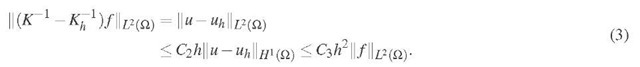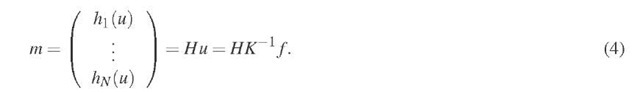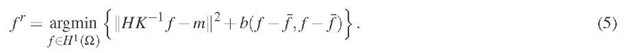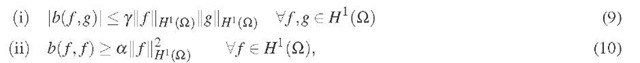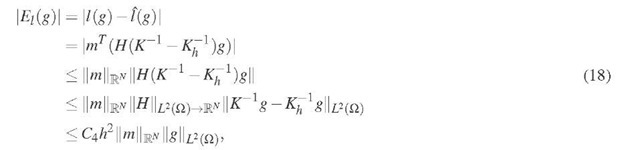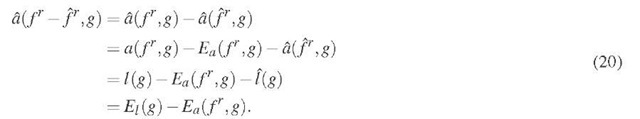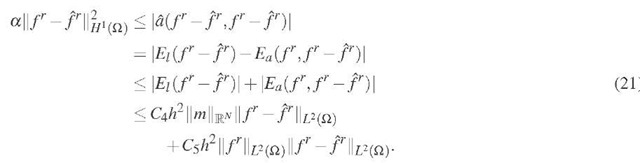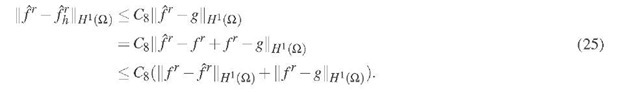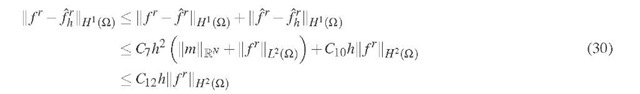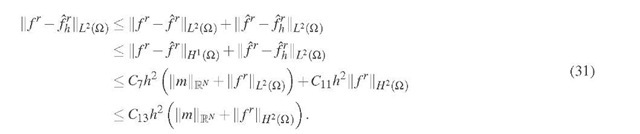Abstract
Many inverse problems arising in experimental mechanics involve solutions to partial differential equations in the forward problem, typically using finite element methods for those solutions. Given that iterative solutions to the inverse problem then involve repeated evaluations of the finite element model, it is useful to carefully consider the mesh to be used and its effect on the trade-off between accuracy and computational cost of the solution. We show that approximation theory can be applied directly to the inverse problem, not merely to the finite element model contained in the forward problem, to give bounds for the error made by using a given mesh to approximate the solution to the partial differential equation. Adaptive mesh refinement allows to focus computational effort on goals set by the quantities of interest in the inverse problem, rather than on the overall accuracy of the solution to the forward problem.
Introduction
Inverse problems —in the sense of problems that, by Hadamard’s criteria[1], are ill-posed whereas the corresponding forward problem is well-posed— occur in many different guises in experimental mechanics, although they are not always recognized as such. For example, the whole family of full-field measurements, including methods based on photoelasticity, moire fringes, in-terferometry, digital image correlation, et cetera, represent ill-posed inverse problems of determining a continuum field variable from a large but finite set of measurements. Conversely, the name inverse problems is widely used in experimental mechanics to refer to parameter identification problems which are not necessarily ill-posed. Determining linear elastic material parameters from mechanical tests with full-field measurements is well-posed if the experiment is not too poorly designed, but using those same measurements to characterize nonlinear constitutive behaviour such as elastoplastic deformation[2] can be ill-posed.
The inherent ill-posedness of full-field measurements is typically resolved without much fuss by implicitly or explicitly taking the spatial resolution of the measurement method into account in the conceptual definition of the field that is measured. Often, the inverse problem is not even considered at all, and the device is simply assumed to provide a means for sampling the continuum field. Nevertheless, there is a growing awareness that conversions between different representations of a continuum field can be problematic[3], and that there are significant advantages to considering the entire measurement process in the inverse methods[4, 5].
Often, the forward problems involve the solution of elliptic partial differential equations, such as the equations of continuum mechanics or the Fourier heat flow equation. These give rise to a particular form of ill-posedness related to Saint Venant’s principle: with increasing distance between load and response, the effects of local details in loading become increasingly difficult to discern. Therefore it is pointless to try to extract too much detail from an inverse method, and it makes sense to search instead for a regularized inverse of the forward problem. For numerical calculations, the forward problem is typically discretized using a finite element approximation, which then raises the question, if it is not useful to extract fine details from the calculation, whether it is necessary to calculate those details at all. In other words, does refining the finite element mesh have the same effect on the accuracy of the solution to the inverse problem as on the accuracy of the solution to the forward problem?
Forward problem
Using the terminology of heat diffusion, the problem we consider is that of reconstructing the heat sources based on a number of temperature measurements. This problem might arise when using infrared thermography for non-destructive testing, or in postprocessing thermoelastic stress analysis data[6]. More importantly, the diffusion equation with different terminology describes many different physical processes. The heat equation serves here as a prototype elliptic partial differential equation; the methods used and the resulting conclusions will be more generally applicable.
Our model for the transfer of heat is Poisson’s equation
where f is the heat source field, a is the thermal conductivity and u is the temperature field.
With suitable additional assumptions [7, 8], there exists a unique solution to this problem for each
be the solution operator to the problem, such that
be the finite element solution operator with mesh density parameter h, and let the corresponding FE solution be denoted
Assuming full regularity and a first order FE approximation, the standard finite element H1 error estimate then gives
and the Aubin-Nitsche lemma gives
The temperature measurements are modeled as linear functionals on the temperature field. That is, the measurement is a vector m such that
For technical reasons, the measurement functionals are assumed to be square integrable, i.e.
Inverse problem
In the inverse problem, a reconstruction fr of the heat source field f is determined from a measurement m. The relation in equation (4) is not uniquely invertible, but a reconstruction is possible with additional assumptions. Often in practice there is some a priori knowledge of the expectation value of f, as well as of its covariance operator. The expectation value of f is denoted by f, and the covariance operator by b(-, •). In addition, since we are interested in enforcing the smoothness of the reconstruction, it will be sought from the Sobolev space H1 (ft).
With these assumptions, then for instance by using the method of statistical inversion or generalized Tikhonov regulariza-tion, a reconstruction can obtained as the following minimization problem [9]
The term
in the minimization hence enforces that f is close to f and that the difference f — f is smooth. This minimization problem can equivalently be written in variational form as: find
such that
where
and
Given that the covariance operator b(-, •) is (i) continuous and (ii) coercive in
it follows that the bilinear form a(-, •) is continuous and coercive. Due to the Lax-Milgram lemma, the problem in equation (6) therefore has a unique solution [7, 8]. However, because both a( , •) and /(•) contain the solution operator K—1 of the forward problem, they cannot be computed with finite resources. To obtain a computable problem close to the original problem, we modify a(-, •) and /(•) to use the FE solution operator
instead.
The modified problem is then: find
such that
where
and
Like , •), the bilinear form &(•, •) is also continuous and coercive in the space H1 (ft), and again by the Lax-Milgram lemma, the variational problem in equation (11) has a unique solution. This problem can then be discretized using Galerkin’s method [7], by choosing a suitable finite subspace
and solving the variational equation in that space, to find
such that
For practical reasons, we choose to build our space Fh on the same mesh, using the same polynomial order in the shape functions, as in the finite element solution of the forward problem.
Error Analysis
The error of the approximate solution
can be broken down into two components
The first part, the term
, is due to using the FE approximation of the forward problem instead of the exact one. We refer to this error source as the consistency error. The second part,
is the discretization error of seeking the solution only from a finite subspace.
To estimate the consistency error, we define two operators
and
The operator Ei(•) can be estimated as
where the last inequality is due to the Aubin-Nitsche L2 error estimate of the finite element solution (3). The operator Ea(•, •) can be estimated similarly to give
Using the definitions of fr and fr, we see that for any
it holds that
Then, due to the coerciveness of a(, •) and the estimates for Ei(•) and Ea(-, ), we can estimate the consistency error as
Combining the constants and estimating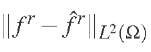
with a stronger norm gives
which finally gives
To estimate the discretization error, we note that since a(-, •) is continuous and coercive in the space „
Cea’s lemma [7, 8] holds true. It states that, up to a constant factor Cs, the discrete solution
is the best approximation of
i.e. for any
Since we want to compare the error to the norm of fr rather than fr, we do the following
Now, since we assume that fr has full-regularity and because Fh is a first order finite element space, there exists an interpolating function g e Fh such that
In addition, we can estimate the term
with the consistency error estimate in equation (23), to obtain
Combining the constants and assuming h < 1 gives
An L2 error estimate follows from the Aubin-Nitsche lemma [7] applied to the variational problem in equation (11). It then holds that
Combining the consistency error and the discretization error, we get the following estimates
and
Numerical experiments
Numerical tests were run in the rectangular domain
The measurements were average temperatures over discs of radius 0.1 (the average is to ensure that they are L2 continuous), which were scattered in a uniform 16×4 grid. The measurement data vector m was simulated on a highly refined mesh using a smooth temperature source field. The bilinear form b( , ) was chosen as
Figure 1 shows three numerical solutions of this problem with different mesh resolutions. The larger features are already present on the coarsest mesh, whereas small details first appear on the second mesh and are further refined on the densest mesh.
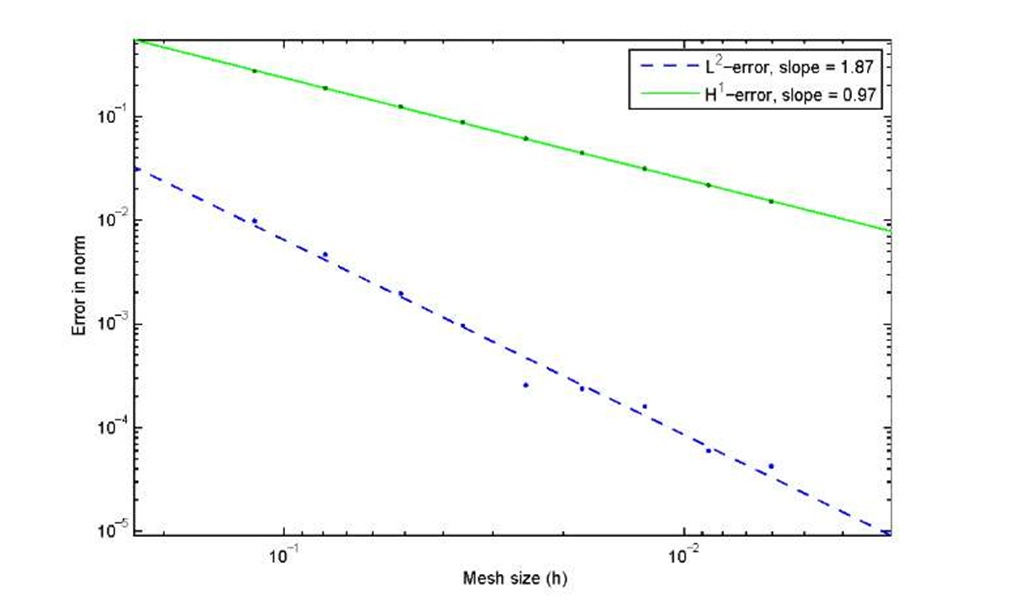
The behavior of H1 and L2 errors against the mesh density parameter h are shown in figure 2. Two straight lines are fitted to the individual computations to derive the convergence rate. For the L2 error, we see convergence in the order of h187, which, is reasonably close to h2 as the analysis predicted. The H1 error also shows a convergence rate quite close to the predicted rate. These errors were computed against a highly refined numerical solution, which acted as the exact solution.
Figure 1 shows three numerical solutions of this problem with different mesh resolutions. The larger features are already present on the coarsest mesh, whereas small details first appear on the second mesh and are further refined on the densest mesh.
The behavior of H1 and L2 errors against the mesh density parameter h are shown in figure 2. Two straight lines are fitted to the individual computations to derive the convergence rate. For the L2 error, we see convergence in the order of h187, which, is reasonably close to h2 as the analysis predicted. The H1 error also shows a convergence rate quite close to the predicted rate. These errors were computed against a highly refined numerical solution, which acted as the exact solution.
Figure 1: Approximate solutions of the inverse problem with an increasing mesh resolution
Figure 2: L2 and H1 errors of the approximate solution with different values of h. The convergence rates correspond well with the rates estimated a priori.
Conclusions
By formulating the inverse problem as a minimization problem similar to the weak form of the finite element problem, the a priori error analysis of the inverse method can be carried out similarly to the error analysis for finite element methods. Errors arise both due to discretizing the quantity of interest and due to using a FE approximation of the forward problem.
Using the same approximation order, the consistency error —i.e., the error due to replacing the exact forward problem with a finite element approximation— is at most the same order of magnitude as the inverse problem discretization error. In fact, in the "natural" H1 norm, it is a full order of magnitude smaller. This suggests that the accuracy of the forward problem is not as critical as usually thought. One should choose the discretization with just enough resolution so that expected features of the reconstruction can be represented.
