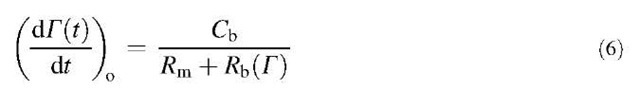INTRODUCTION
In this review, we focus on the role of surface heterogeneity in polymer adsorption and discuss novel experiments that clarify the impact of topographical and chemical heterogeneity on adsorption of flexible polymers and globular proteins. The comparison of the experimental results with existing theoretical predictions provides valuable insights into the adsorption process and guides future development of theory and experiments. Furthermore, these results provide a starting point for more sophisticated design and control of polymer adsorption at the nanoscale and in engineering of surfaces to achieve specific tasks.
The importance of polymer and protein adsorption stems from its critical role in a host of industrial applications such as adhesion, biocompatibility, colloidal stabilization, and chromatography. Scientifically, the in-terfacial behavior of globular proteins and long, flexible macromolecules and the accompanying balance of en-thalpic and entropic effects from surface-segment interactions provide a system replete with interesting static and dynamic phenomena. Consequently, adsorption of polymers and biopolymers at a solid-liquid interface has been the subject of intense investigation over the last decade.
Despite the advances in characterization and theoretical understanding of near-equilibrium properties of adsorbed polymer layers, several aspects of the adsorption process remain elusive.[1-3] Among these elusive aspects is the effect of nanometer scale compositional and topographical heterogeneity of surfaces (Fig. 1a) on the process of adsorption and the structural properties of the adsorbed layer. Because adsorption frequently occurs on real surfaces such as minerals, pigments, colloidal particles, and biological membranes that are inherently heterogeneous, understanding the impact of surface heterogeneity is an essential prerequisite to controlling the adsorption process.
BACKGROUND
Modeling of Transport and Adsorption of Macromolecules
Adsorption at a surface occurs from a bulk polymer solution if the net change of free energy is negative. The surface-segment contacts of the polymer provide a gain of adsorption energy to balance the loss of translational and conformational entropy from the confinement at the interface. The properties of the adsorbed layer depend not only on the thermodynamic details of the system but also on the adsorption history.[4] Therefore control of adsorption requires a complete understanding of adsorption kinetics and the role of the surface.
Three main steps are typically involved in polymer adsorption: mass transport toward the surface, surface attachment, and spreading or conformational rearrangement toward equilibrium configurations.[1-3] The driving force for transport from bulk solution is the gradient between the bulk solution concentration (Cb) and the subsurface concentration (Cs). Because the gradient is established rapidly in most cases, the flux of the polymer can be
where the mass transfer resistance (Rm) depends on the convection-diffusion in bulk solution. Rm can be expressed as 1/km, where km is the mass transfer coefficient. Cs depends on the surface excess (G) of the polymer and its temporal evolution
The processes of penetration of a chain through an already adsorbed layer of polymer, attachment to the surface, and spreading on the surface determine the barrier resistance At pseudo-steady state, the flux and the rate of adsorption are equal, which gives
Fig. 1 Schematic of (a) a heterogeneous surface and (b) evolution of the surface excess (G).
During the formative stages of an adsorbed layer, Rm should dominate and for high-affinity adsorption, Ceq ~ 0. Therefore the initial rate of adsorption becomes
and G(t) typically shows a linear rise (Fig. 1b). Over a longer period equilibrium is established and G(t) reaches a plateau, which is determined by parameters such as solvency, Cb, surface-segment interaction, and molecular weight.
Adsorption on Heterogeneous Surfaces: Theoretical and Simulation Studies
In previous theoretical studies on the role of physical heterogeneity, rough surfaces were modeled as random, fractal, and periodically structured.[6-10] Most of these studies came to the conclusion that adsorption is enhanced with surface roughness. Ji and Hone[11] predicted that the enhancement is most significant when amplitudes and spatial size of roughness are of the order of a polymer chain or Kuhn length, which is of nanometer dimensions.
The enhancement occurs as larger adsorption energy is gained by increasing probability of polymer-surface intersections in comparison to a smooth planar interface. Consequently, a polymer chain undergoes smaller distortion and configurational entropy penalty is also predicted to be less relative to adsorption on flat surfaces. These studies predicted that a polymer can adsorb on a rough surface and not on a flat surface even if the chemical interface is identical.
More recent investigations1-12-1 have explored the role of polymer architecture in adsorption on rough surfaces. Striolo and Prausnitz predicted that adsorption occurs readily for branched polymers compared to linear polymer chains because a smaller entropic penalty is involved for adsorption of globular polymers. However, when the interaction between polymer segments and surface becomes strong enough, it was predicted that a linear polymer chain can spread more than the globular polymer as the entropic loss is overcome by the gain in adsorption energy from spreading. Thus for highly attractive segment-surface interactions, linear polymers are believed to adsorb strongly compared to globular polymers.
In previous theoretical studies, the influence of chemical heterogeneity on adsorption varied with the systems. The chemical heterogeneity of the surfaces was manipulated by changing the distribution, size, and shape of the heterogeneity.[13-18] Meanwhile, several types of polymers such as a homopolymer, a block-copolymer, and an end-sticking polymer were employed in simulations. Heterogeneous interaction between polymer and surfaces was predicted to be a larger weighing factor than physical heterogeneity in polymer adsorption.[19] Several remarkable effects were found in these studies. First, the heterogeneity on the surfaces induced adsorption even when the average surface was neutral. It was predicted that adsorption was enhanced for homopolymers because of the presence of heterogeneity. Second, most studies pointed out that the distribution and size of adsorbing sites and nonadsorbing sites play a crucial role. Again, the domain size was required to be commensurate to that of polymer chains. When a threshold value of either the distribution or the size of domains was reached, polymers responded to the surface in dramatically different ways. This was reflected in the adsorption behavior, the amount, and the arrangement of polymers on the surfaces. In the case of homopolymers, van der Linden and coworkers showed that a mere change in the distribution of sites could cause a nonadsorbing surface to become adsorbing. Sumithra and Sebastian observed a sudden change in the size of an adsorbed polymer. In the case of block copolymers and end-sticking polymers, change of domain sizes on the surface caused segregation of polymers in a uniform adsorbed layer.
In addition to the focus on homopolymers and copolymers, recent studies have used Monte Carlo simulation and replica field theory to explore the adsorption behavior of random heteropolymers (RHPs) on chemically heterogeneous surfaces.[20,21] Striking recognition between polymers and random surfaces has been predicted. A sharp transition from weak to strong adsorption was seen when the statistical sequence of chain segments and the randomness of sites on surfaces were related. Similar instances of pattern matching have also been predicted during adsorption of charged polyelectrolytes on surfaces with a pattern of charges.[22] Recently, Genzer developed a three-dimensional self-consistent field lattice model to study adsorption of copolymers and showed that architecture as well as composition is important in the pattern recognition.[23] By using different copolymers such as alternating, diblock, and triblock copolymers with various ratio of adsorbing segments, chemical heterogeneity on surfaces could either be masked or amplified and recognition could be extended into the third dimension normal to the surface.
Thus theory and simulation based on statistical physics has explored extensively the influence of both chemical and physical heterogeneity on the adsorption behavior of polymeric chains. However, corroboration by systematic and well-defined experiments to test and exploit these predictions has been nonexistent. The bottleneck for realizing actual systems lies in the difficulty of manipulating heterogeneity on a size scale that is commensurate with that of a polymer chain (typical radius of gyration of 10-100 nm). By modifying and characterizing surfaces at a molecular level, we have carried out the first studies to overcome the experimental challenges. The next few sections review these experimental results.
IMPACT OF NANOMETER SCALE PHYSICAL HETEROGENEITY
In recent years, synthesis of surfaces and control of interfacial properties has been transformed by the use of self-assembled monolayers (SAMs).[24] Their excellent chemical stability, low defect density, and spontaneous formation permit the preparation of a well-defined interface on a molecular level, easily and reproducibly. We have addressed the challenge of preparing physically heterogeneous surfaces that are commensurate with the typical dimensions of a polymer chain and are chemically homogeneous.[25] The approach exploits ultraflat, template-stripped gold films and rough, evaporated gold films supporting self-assembled monolayers. In addition, a surface plasmon resonance technique that permits in situ measurements at the solid-liquid interface with high time resolution is used to investigate the kinetics of adsorption. With these two tools, we have studied in detail the adsorption of a flexible, uncharged polymer such as poly (ethylene oxide) (PEO) and established the interplay between physical heterogeneity, the polymer flux to the surface, and the polymer chain length.[26]
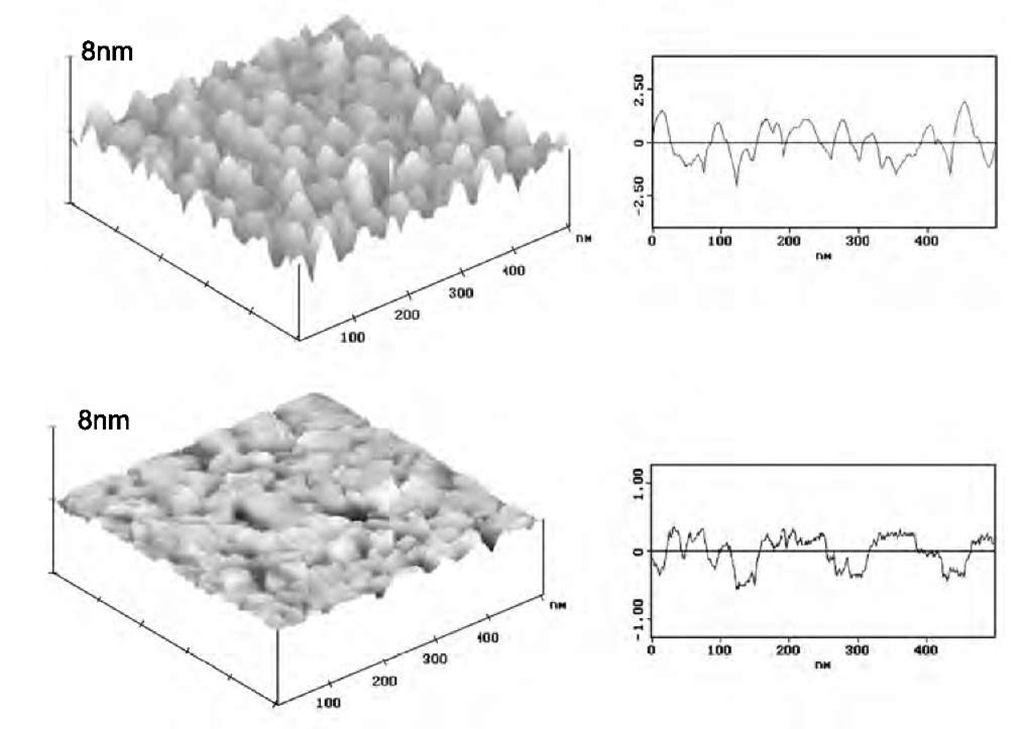
Fig. 2 STM image and cross section of a rough gold substrate (top) and an ultra-flat gold substrate (bottom).
Fig. 2 shows the typical surface plot and cross-section analysis of a rough and an ultraflat gold substrate. When compared to cases considered by past theoretical studies of adsorption on physically heterogeneous surfaces, the images show that the experimental system here represents a case of polymer adsorption onto a random surface rather than a periodically structured surface. Both substrates possess a grainy but distinct surface texture, which indicates that the spatial distribution of surface roughness differs for the two surfaces. The evaporated rough gold substrate shows a larger range of feature heights compared to ultraflat template-stripped substrate.
Because the surfaces are characterized by small vertical deviations in surface topography with high spatial complexity, the variation of root-mean-square roughness Rrms with the lateral length-scale was analyzed. The variational Rrms for the rough and ultraflat gold substrates increases as the lateral length scale increases above 10 nm and becomes independent beyond a spatial scale of 60 nm. This macroscopic value is Rrms ~ 8 A for the rough gold substrate and Rrms ~ 3 A for the ultraflat surface, which is perceived in the real-space images as a difference in vertical heights. Between 10 and 60 nm, the geometric complexity of the surfaces is fractal-like and the fractal dimension (DF) for rough gold substrate is approximately 2.25 and for ultraflat substrate is approximately 2.15. Because of this fractal-like nature, the relative area of peaks and valleys on the surfaces shown in Fig. 2 changes with the image size for lateral length scales below 60 nm. This length scale is commensurate with the typical dimensions of a polymer chain. Furthermore, the vertical deviations in height for both surfaces are comparable to the size of a few monomers along the polymer chain over a wide spatial extent. The topography of these surfaces is well suited to test the predictions of theoretical studies.
In order to ensure that the two gold substrates have identical chemical interface, a self-assembled monolayer of dodecanethiol (CH3(CH2)11SH) was formed on both substrates. The advancing contact angle (0a) of hexade-cane on the resulting surfaces was 46-47°, which is consistent with an interface of densely packed CH3 groups. The receding contact angles (0r) for the mono-layers supported on the rough gold substrate showed a contact angle hysteresis of 4° and the monolayers on the ultraflat substrate gave a hysteresis of 1°. These different values of hysteresis reflect the differences in the topography of the substrates supporting the monolayers.
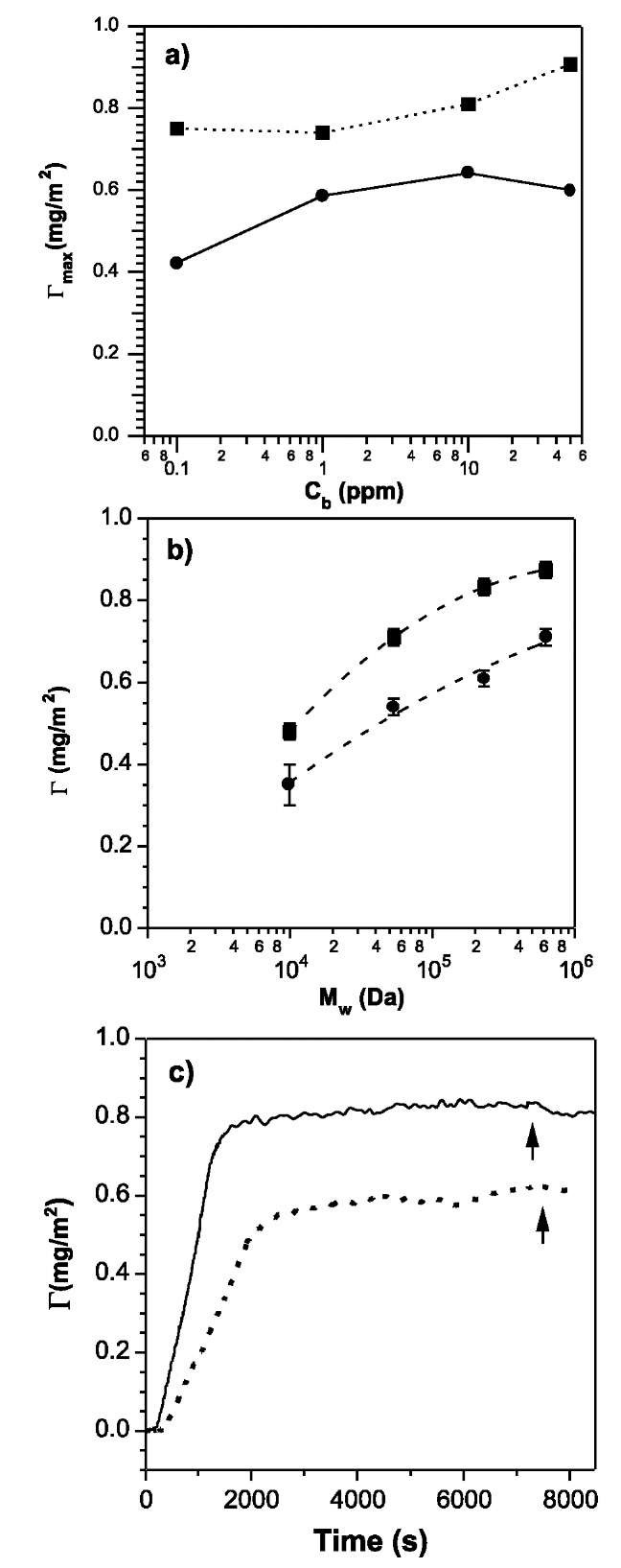
Fig. 3a shows the adsorption isotherm for PEO with a molecular weight (Mw) of 53.5 kDa. PEO has similar maximum surface excess (Gmax) at low and high bulk concentrations, which indicates high affinity adsorption behavior on both surfaces [Eq. 4]. Fig. 3b shows the effect of molecular weight on the adsorption amount in the plateau regime for a bulk concentration of 1 ppm. Higher Mw gives slightly larger adsorption amounts. This is generally because longer polymer chains can form longer loops and tails than shorter chains, as predicted by the Scheutjens-Fleer model.[1] The dependency of adsorption amount on molecular weight is stronger for shorter chains and approaches a limit for longer chains. Rough gold surfaces and ultraflat surfaces possess the same degree of hydrophobicity but different extents of surface roughness. Interestingly, plateau adsorption amounts on ultraflat surfaces are 20-30% lower than that on rough surfaces for the various molecular weights investigated. These results indicate that the maximum surface excess of the polymer increases because of the presence of physical heterogeneity. This is the first experimental corroboration of the theoretical predictions that adsorbed amount of a polymer increases with surface roughness.
The surface area occupied by a PEO chain on the surface can be estimated from
The lower values of Gmax in Fig. 3b for the ultraflat surfaces lead to higher area per chain and indicate that the adsorbed polymer chains flatten slightly more on the smooth substrates relative to the rough surfaces. Because the spreading of chains on ultraflat surfaces will occur on time-scales that are characteristic of the polymeric system and the adsorption conditions, it is useful to analyze the evolution of G(t). Fig. 3c shows the evolution of G(t) for a PEO chain (Mw=230.7 kDa) on rough and ultraflat surfaces. Both adsorption curves resemble the schematic G(t) shown in Fig. 1b. However, the effect of physical heterogeneity is clearly revealed in the initial adsorption rate, which is higher on rough surfaces. Except for a very short PEO (~ 10 kDa), the difference A(dG/dt)o is manifested in the adsorption of several different PEO ranging from 53.5 to 624 kDa.
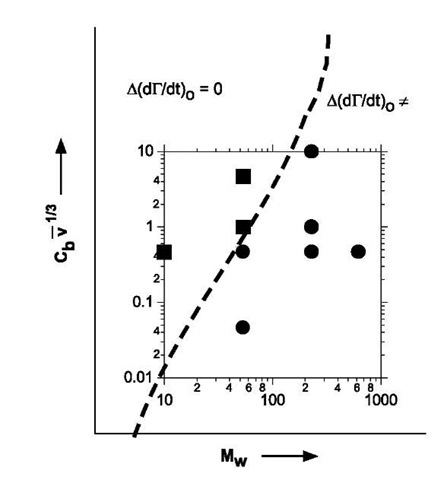
Because the adsorption occurs under the same flow and concentration conditions (i.e., Rm and Cb), the simplified Eq. 4 cannot be used to interpret the difference A(dG/dt)o. Instead, the experimental results suggest that is more appropriate for the ultraflat surface and that a finite resistance Rb due to spreading, attachment, and penetration of polymer chains leads to a lower initial rate of adsorption. This conclusion is supported by a disappearance of the difference in initial rate of adsorption as the bulk concentration Cb and the bulk flow velocity is increased (Fig. 4). Physically, the polymer flux increases as J/ Cb and km/v1/3. As a consequence of the rapid transport of chains to the surface, the spreading of the chains on ultraflat gold during the initial stages of adsorption is suppressed and no difference in initial rate is observed. Fig. 4 shows that this interplay between transport effects and reorganization of polymer chains on the surface is a function of the length of the polymer chain. In contrast to PEO of Mw=53.5 kDa, it is significantly harder to suppress the difference in (dG/dt)o by increasing the convective flux via Cbv1/3 for long chains. On the other hand, for low molecular weight materials, the difference in the rate of adsorption is not observed because of the progressive difficulty in accessing very low values of Cbv1/3 in the experimental window.
Fig. 3 Adsorbed amount of PEO as a function of bulk concentration in solution (a) and molecular weight (b) on rough surfaces (squares) and ultra-flat surface (circles). (c) An illustration of G(t) for PEO adsorption on rough (solid line) and ultra-flat (dashed line) surfaces.
As chain length impacts the structure of the adsorbed layer, at this stage it is not possible to attribute the variation in kinetic effects with Mw to either the interaction potential between the polymer and the surface or the time scale of spreading. While the experiments on physically heterogeneous surfaces corroborate theoretical predictions, they also underscore the need for development of new kinetic models that will not only aid in interpreting results such as those presented here but also guide newer experiments for understanding polymer adsorption at an interface that is heterogeneous on the nanometer scale.
Fig. 4 Plot showing interplay between Mw and convective flux on the difference in initial rate of adsorption for rough and ultra-flat surfaces (see text for discussion). Experimental points are shown as symbols.