IN WHICH we continue our discussion of the theoretical framework of GPS position finding, and you practice using PC software to investigate files collected by GPS receivers.
OVERVIEW
Some Questions Answered
As you read the last two topics some questions may have occurred to you. And the answers to these questions may generate other questions. Here are some that come up frequently:
Question #1: "The captain of the ship of Figure 2-1 had a map showing the locations of the soundhouses. But how does the GPS receiver know where the satellites are?"
A map is a two-dimensional scale model of the surface of the Earth. But models can take many forms, including mathematical. Due to the nature of nature, as elucidated by Isaac Newton and Johannes Kepler, the position of a satellite at any time may be predicted with a high degree of accuracy by a few mathematical equations. A satellite orbiting the earth may be modeled by formulas contained in the memory of the microcomputer in the receiver. When the formulas are applied to bodies at the high altitudes of the GPS satellites, where they are free from atmospheric drag, the formulas are relatively simple and can predict the position of the satellite quite accurately.
Almost all formulas have a general form, into which specific numbers are "loaded." For example, in an equation of the form
A and B are parameters which represent constant numbers that may be inserted in the equation. When A and B are replaced by actual numbers, then the equation is only true for certain values of x, y, and z. The receiver carries the general form of the formulas that give the position of each satellite. Before the range readings are taken by the receiver, the satellites will have broadcast the values of their particular parameters so the receiver can complete its equations. Then, by knowing the current time at a given moment (the moment at which the distance reading is taken), the receiver can know where the satellites are.
Actually, the satellite message coming to the receiver antenna is in many parts. Two of these might be called the almanac and the ephemeris data. Almanac information is broadcast to provide close, but not precise, satellite position information. The almanac for all satellites is broadcast from each satellite. Furthermore, each satellite broadcasts ephemeris information (which applies to that satellite only), that provides up-to-the-minute corrections. The satellites are not completely predictable in their orbits because of such forces as gravitational pull from the sun and moon, the solar wind, and various other small factors. Therefore the satellites are carefully monitored by ground stations and told their positions; each satellite then rebroadcasts this information to GPS receivers.
Question #2: "The captain needed to know exactly what time it was in order to determine his distance from the soundhouse. How is the clock in the receiver kept accurately on GPS time?"1
The short answer is that the receiver clock is reset to GPS time by the satellites each time a position is found. Such resetting is necessary because, while the receiver clock is very consistent over short periods of time, it tends to drift over longer periods. (Each of the four atomic clocks in each satellite costs about $50,000; the single clock in the receiver obviously costs a whole lot less, so you can’t expect the same sort of accuracy. If you don’t use the receiver for a week or two, you may notice a difference of several seconds between the time the receiver displays and true time.) The clocks in the satellites keep time to about a tenth of a billionth of a second (a tenth of a nanosecond).
If you consider "time"2 as the 4th dimension and accept that it takes one satellite to fix each dimension, then it is clear that four satellites, working in concert, can set the clock and provide a 3-D spatial position.
Recalling our discussion of the theory of GPS and from the geometry of the diagrams you examined, you might presume that only three satellites are required for a 3-D fix. But given that the receiver has only an approximate idea of what time it is, what must be calculated is a 4-D fix. So four satellites are required. It is not correct to say that three satellites are used for the 3-D fix and the fourth sets the receiver clock. Rather, all of the satellites operate in concert to find the true "position" of a receiver antenna that may move in space (relative to the earth) and does move in time.
GPS, as previously mentioned, has had a revolutionizing effect on the business of keeping extremely accurate time—to better than a billionth of a second. While most of those who use GPS are concerned with finding positions, the system also supplies extremely accurate time signals to receivers whose positions are known with high precision. GPS has made it possible to synchronize clocks around the world. This has made it possible, among other things, to gain knowledge about the makeup of the earth’s center. Since seismologists throughout the world know the exact time, they can track the shock waves from earthquakes as they pass through the earth. Another use of the ability of GPS to synchronize clocks around the world is in routing Internet (worldwide web) traffic. It would not have been unreasonable to have called GPS by the acronym GPTS: the Global Positioning and Timing System.)
Question #3: "The soundhouse sent a signal every minute. How often does a satellite send a signal? What is the signal like?"
Actually, each satellite sends a signal continuously, rather like a radio station broadcasts 24 hours per day. The radio station signal can be considered to consist of two parts: a carrier, which is on all the time, and "modulation" of that carrier, which is the voice or music that you hear when you listen to the station. (You probably have detected the presence of the carrier when the people at the station neglect to say or play anything.3 The carrier produces silence, whereas if your radio is tuned to a frequency on which no nearby station is broadcasting you will hear static.)
Each satellite actually broadcasts on two frequencies. Only one of these is for civilian use. (The military GPS units receive both.) The civilian carrier frequency is 1575.42 megaHertz (1,575.42 million cycles per second). In contrast, FM radio signals are on the order of about 100 megaHertz. So the GPS radio waves cycle about 15 times as often, and are, therefore, one-fifteenth as long: about 20 centimeters from wavetop to wavetop. As this goes to press there is serious discussion about adding one or two new civilian signals. Having two signals at different frequencies available allows a receiver to compute a more accurate position than does a single signal.
The modulation of the GPS wave is pretty dull, even when compared to "golden oldies" radio stations. The satellites broadcast only "bits" of information: zeros and ones. For most civilian use, this transmission, and the ability to make meaning out of it, is called the "C/A code"—standing for Coarse/Acquisition code. The word "Coarse" is in contrast to another code used by the satellites: the "P" or "Precise" code. The term "Acquisition" refers the capability that allows both civilian and military receivers to acquire the approximate position of the receiver antenna. The C/A code is a sequence of 1,023 bits which is repeated every one-thousandth of a second.
A copy of the C/A code for a given satellite might look like this:
1 0 0 0 1 1 0 1 0 0 1 0 1 1 1 1 0 1 1 0 0 0 1…
and on and on for a total of 1,023 bits. Then the sequence starts again. The sequence above probably looks random to you—as though you began flipping a coin, recording a "1" each time it came up heads and a "0" for tails. It is, in fact, called a pseudorandom noise code—the term "noise" coming from the idea that an aural version of it would greatly resemble static one might hear on a radio. The acronym is PRN.
Question #4: "How does the receiver use the 0s and 1s to determine the range from the satellite to the receiver?"
The PRN code is anything but random. A given satellite uses a computer program to generate its particular code. The GPS receiver essentially uses a copy of the same computer program to generate the identical code. Further, the satellite and the receiver begin the generation of the code at exactly the same moment in time.
The receiver can therefore determine its range from the satellite by comparing the two PRN sequences (the one it receives and the one it generates). The receiver first determines how much the satellite signal is delayed in time, and then, since it knows the speed of radio waves, it can calculate how far apart the two antennas are in space.
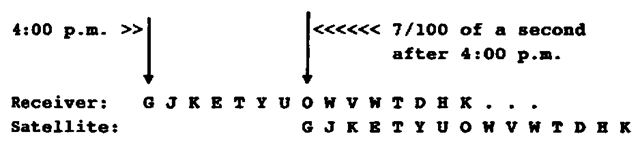
As an example (using letters rather than bits so we can have a more obvious sequence, and cooking the numbers to avoid explaining some unimportant complications), suppose the satellite and the receiver each began, at 4:00 P.M., to generate one hundred letters per second:
G J K E T Y U O W V W T D H K…
The receiver would then look at its own copy of this sequence and the one it received from the satellite. Obviously its own copy would start at 4:00, but the copy from the satellite would come along after that, because of the time it took the signal to cover the distance between the antennas. Below is a graphic illustration of what the two signals might look like to the computer in the receiver:
The receiver would attempt to match the signals. You can see that the signal from the receiver began to arrive seven letters later than 4:00; the receiver’s microcomputer could therefore determine that it took 7/100 of a second for the signal from the satellite to reach the receiver antenna. Since the radio wave travels at about 300, 000 kilometers per second, the time difference would imply that the satellite was 21,000 (that is, 7/100*300,000) kilometers from the antenna.
Question #5: "The receiver must find ranges from at least four satellites to determine its position. How does the receiver "listen to" several satellites at once? Since all satellites broadcast on the same frequency, how does the receiver identify the satellites?"
The first thing to know is that each satellite has its own distinctive PRN code. In fact, the satellite numbers you were logging in the first assignment were the PRN numbers—which is the principal way satellites are identified. A satellite may also have a number painted on its side, but it is the PRN number that counts. When an older satellite is retired, its replacement can take on its PRN number.
Most receivers have several electronic components, called "channels," that are tuned to receive the civilian GPS frequency. Although all channels are tuned to the same frequency, a single channel can track a GPS satellite by locking onto its PRN code. In more expensive receivers with several or many channels, each channel is assigned full time to tracking a single satellite. Other receivers "time-share" a channel—flipping it between satellites, as you might flip between channels on a TV, trying to keep track of two programs at once.
Question #6: "I’ve heard that the accuracy of GPS receivers was greatly increased recently when selective availability was turned off. What was selective availability? Why did it exist?"
Selective Availability, or SA, was the error deliberately introduced by the GPS managers in the C/A code broadcast to diminish the accuracy of GPS receivers. Sometimes the satellites lied about their positions. Sometimes they lied about when they sent the code.
What was the extent of the error caused by SA? The government guaranteed that 95% of the time a fix would be within 100 meters of the true position. To understand why SA existed you have to realize that the NAVSTAR system started as a military project to provide navigation for units of the armed forces. In the broad sense, GPS was designed as a weapons support system. One doesn’t want one’s weapons to fall into enemy hands. So steps were taken to deny use of the system to all but authorized receivers. In fact, the very existence of the GPS system, whose first satellite was launched in 1978, remained secret for several years.
It was never planned that you could buy a $200 receiver for your fishing boat. The military feared such uses as a terrorist with a mortar knowing exactly where he was, and hence being able to more accurately target his fire. Or the computer in a missile being able to monitor its position and correct its path during its flight.
If sufficient warning were given, of course, the entire civilian side of NAVSTAR could be shut down to deny its use to hostile forces. (The consequences would be disastrous, but not as much so as a nuclear war.) But, in any event, the military was still uncomfortable with allowing the best GPS accuracy in the hands of everybody. So why was SA turned off? As it turns out, very good accuracy may be obtained by using two GPS receivers in concert and for the very best accuracy you need two receivers, SA or no. So SA became more of a nuisance that offered no real protection. In fact, the Army Corps of Engineers began broadcasting corrections to positions obtained by civilian receivers. Under pressure from the civilian GPS users, and other countries—Japan and European—who began contemplating their own version of GPS, using the more general term Global Navigation Satellite System (GNSS)4—the U.S. government abruptly clicked the SA switch off. This occurred on 2 May 2000, just after midnight Eastern Time. It was an important enough decision that the President made the announcement himself. The slim protection SA provided might be replaced and enhanced by jamming the GPS signals in selected geographical areas, if necessary. If you are interested in SA, and other matters related to GPS policy, you can go to the web site of the Interagency GPS Executive Board (www.igeb.gov) and find out considerably more than there is space for here. You can also view the President’s declaration of 1 May 2000.
Question #7: "How is it that a satellite, cutting Earth’s meridians at 55° and moving at 8600 mph, generates a track that is almost due north-south in the vicinity of the equator, as seen in Figure 1-1?"
While the satellite is moving very fast, it is also far out in space. Therefore the motion of the corresponding point on the Earth’s surface along the satellite’s track (picture where a line from the center of the earth to the satellite would intersect the surface of the Earth) is considerably slower—about 2100 mph. The satellite’s track along the surface of the Earth moves at this speed toward the northeast on the upswing and southeast on the downswing, so the eastward part of its motion is in the same direction as the rotation of the Earth. Any given point on Earth’s surface at the equator moves about 1050 miles per hour eastward due to Earth’s rotation about its axis. The north or south component of the satellite’s velocity is about 1700 mph, while the east component is only about 1200 mph. So an observer at the equator would see only a slow drifting (about 150 miles per hour) of the satellite to the east over the period of an hour or two.
Question #8: "If the orbital period is 12 hours, why does each satellite rise and set about four minutes earlier each day? Could the NAVSTAR system designers arrange to have the same satellites in view at the same time each day in a given location?"
The short answer to the first question, if you know a bit of astronomy, is that the satellites orbit the earth twice during a sidereal (pronounced si-dear-e-ul, meaning "star based") day, rather than a solar (sun-based) day. A longer explanation: Suppose you look up at the stars on midnight of the first of April and note their positions. To see the same picture on May first you have to look up at 10:00 P.M. In the 30 days the stars "moved" 120 minutes—four minutes a day. Of course the stars didn’t move; the earth rotated. By midnight it would have turned not only the 10, 800 degrees (that is, 360 per day times 30 days) from its daily rotation, but 30 degrees further (360 degrees multiplied by one-twelfth) from its yearly rotation in its orbit around the sun. The 10, 800 degrees works out to zero basically (you are back where you started from) but the 30 degrees is significant.
Or think of it this way: While each individual satellite is in orbit about the Earth, making its circuit exactly twice a day, the set of satellites are independently in orbit about the sun. They orbit the sun as a package—the rings of their orbit making up sort of a spherical birdcage. The cage is centered on the Earth and contains it. The Earth is a body that rotates independently within this cage. The cage does not rotate at all on its own axis, but orbits the sun.
To understand what "not rotating on its axis" means, realize that the moon rotates on its own axis once during each trip around the earth, so that it always shows the same face to Earth. If the moon did not rotate, we would see different sides of it as it made its way around the Earth. In contrast to the moon-earth situation, consider the cage-sun situation: the cage does not rotate on its axis and therefore does present different sides of itself to the sun over the course of a year.
So at any given time (say noon, when the sun is directly over a given meridian), a person on Earth will see (that is, "look through," toward the sun) one side of the cage on the solstice in January. But from the same point on earth that person would be looking through the opposite side of the cage in July. In effect, then, the cage will be seen from Earth to have made half a complete rotation around the Earth once each half year. To a person on the Earth, then, the cage apparently moves about 1/ 365th of a rotation per day. That amounts to about four minutes a day—calculated as 1440 minutes in a day divided by the number of days in a year.
In answer to the second part of Question #8, if the satellite’s orbits were boosted another 50 kilometers or so further out they would appear in the sky at the same place at the same time each day. The further a satellite is from the earth the longer its period— both because it moves more slowly and because it has further to go.
Question #9: "In earlier text it was suggested that it was somewhat more important that there be a good view of the sky to the south for good reception. Why?"
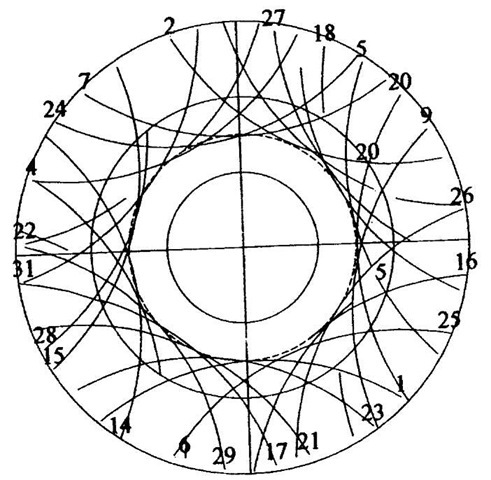
The statement about reception being better toward the south applies only to the middle and upper latitudes in the northern hemisphere. As you know, the satellites are in oblique orbits. Their tracks give the north and south poles a wide berth. In Figure 3—1 you are looking directly down on the north pole at satellite tracks generated over a six hour period. The dashed circle is a parallel at 45°, so you can see that there is a dearth of satellites overhead if you go very far north of that. There is still good GPS coverage—all the way to the North Pole.
Figure 3-1. GPS satellite tracks seen from space looking toward the North Pole.
STEP-BY-STEP
Recall the story of the two "logically challenged" people who rented aboat and went fishing. They were highly successful—catching a lot of fish.Said "A" to "B," "Be sure to mark this spot so we can come back to it." Asthe day ended and they were approaching the dock, "A" asked "B": "Didyou mark that fishing spot?", to which "B" replied: "Sure I did, just like youasked me—right here on the side of the boat" There was a pause as theabsurdity of this penetrated "A’s" brain. ‘You idiot! What if next time wedon’t get the same boat?"
But now, as we move into a new century, you have a way of marking where you were. In fact, you have done so.By use of the program you can determine where you are to within 5 to 15 meters. Our goal now is to look at those uploaded files, and some others, both graphically and statistically. You will also acquire an understanding of the quality of your data.