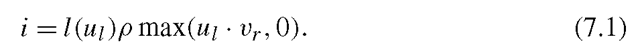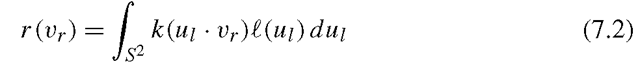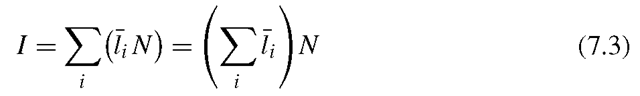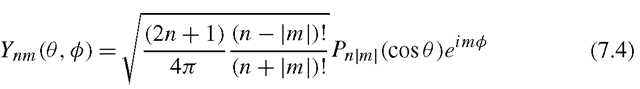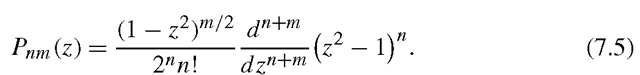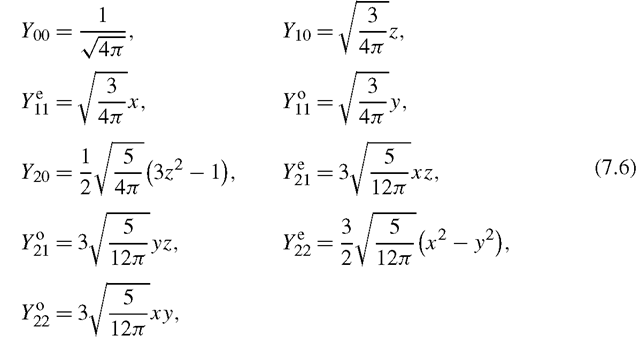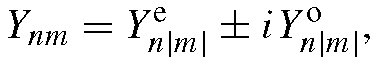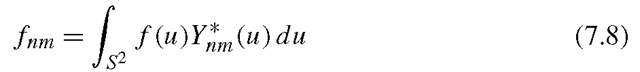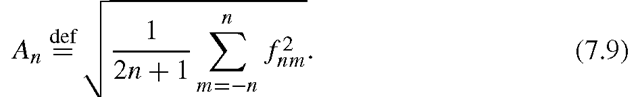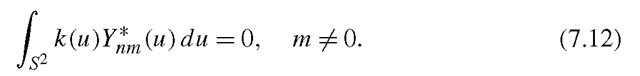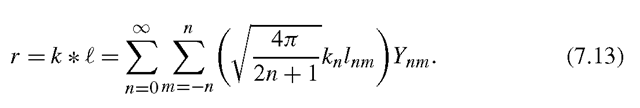Introduction
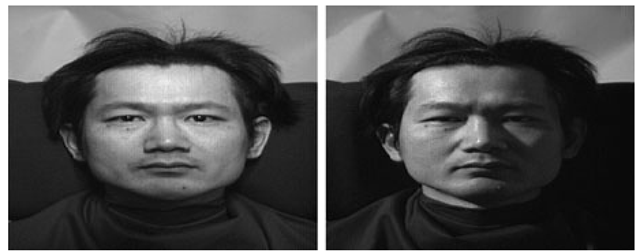
Changes in lighting can produce large variability in the appearance of faces, as illustrated in Fig. 7.1. Characterizing this variability is fundamental to understanding how to account for the effects of lighting on face recognition. In this topic, we will discuss solutions to a problem: Given (1) a three-dimensional description of a face, its pose, and its reflectance properties, and (2) a 2D query image, how can we efficiently determine whether lighting conditions exist that can cause this model to produce the query image? We describe methods that solve this problem by producing simple, linear representations of the set of all images a face can produce under all lighting conditions. These results can be directly used in face recognition systems that capture 3D models of all individuals to be recognized. They also have the potential to be used in recognition systems that compare strictly 2D images but that do so using generic knowledge of 3D face shapes.
One way to measure the difficulties presented by lighting, or any variability, is the number of degrees of freedom needed to describe it. For example, the pose of a face relative to the camera has six degrees of freedom—three rotations and three translations. Facial expression has a few tens of degrees of freedom if one considers the number of muscles that may contract to change expression. To describe the light that strikes a face, we must describe the intensity of light hitting each point on the face from each direction. That is, light is a function of position and direction, meaning that light has an infinite number of degrees of freedom. In this topic, however, we will show that effective systems can account for the effects of lighting using fewer than 10 degrees of freedom. This can have considerable impact on the speed and accuracy of recognition systems.
Fig. 7.1 Same face under different lighting conditions
Support for low-dimensional models is both empirical and theoretical. Principal component analysis (PCA) on images of a face obtained under various lighting conditions shows that this image set is well approximated by a low-dimensional, linear subspace of the space of all images (see, e.g., [19]). Experimentation shows that algorithms that take advantage of this observation can achieve high performance, for example, [17, 21].
In addition, we describe theoretical results that, with some simplified assumptions, prove the validity of low-dimensional, linear approximations to the set of images produced by a face. For these results, we assume that light sources are distant from the face, but we do allow arbitrary combinations of point sources (e.g., the Sun) and diffuse sources (e.g., the sky). We also consider only diffuse components of reflectance, modeled as Lambertian reflectance, and we ignore the effects of cast shadows, such as those produced by the nose. We do, however, model the effects of attached shadows, as when one side of a head faces away from a light. Theoretical predictions from these models provide a good fit to empirical observations and produce useful recognition systems. This suggests that the approximations made capture the most significant effects of lighting on facial appearance. Theoretical models are valuable not only because they provide insight into the role of lighting in face recognition, but also because they lead to analytically derived, low-dimensional, linear representations of the effects of lighting on facial appearance, which in turn can lead to more efficient algorithms.
An alternate stream of work attempts to compensate for lighting effects without the use of 3D face models. This work directly matches 2D images using representations of images that are found to be insensitive to lighting variations. These include image gradients [12], Gabor jets [29], the direction of image gradients [13, 24], and projections to subspaces derived from linear discriminants [8]. A large number of these methods are surveyed in [50]. These methods are certainly of interest, especially for applications in which 3D face models are not available. However, methods based on 3D models may be more powerful, as they have the potential to compensate completely for lighting changes, whereas 2D methods cannot achieve such invariance [1, 13, 35]. Another approach of interest, the Morphable Model, is to use general 3D knowledge of faces to improve methods of image comparison.
Background on Reflectance and Lighting
Throughout this topic, we consider only distant light sources. By a distant light source, we mean that it is valid to make the approximation that a light shines on each point in the scene from the same angle and with the same intensity (this also rules out, for example, slide projectors).
We consider two lighting conditions. A point source is described by a single direction, represented by the unit vector Ul, and intensity, l. These factors can be combined into a vector with three components, I = Iul. Lighting may also come from multiple sources, including diffuse sources such as the sky. In that case we can describe the intensity of the light as a function of its direction, I(Ul), which does not depend on the position in the scene. Light, then, can be thought of as a nonnegative function on the surface of a sphere. This allows us to represent scenes in which light comes from multiple sources, such as a room with a few lamps, and also to represent light that comes from extended sources, such as light from the sky, or light reflected off a wall.
Most of the analysis in this topic accounts for attached shadows, which occur when a point in the scene faces away from a light source. That is, if a scene point has a surface normal vr, and light comes from the direction Ul, when Ul · vr < 0 none of the light strikes the surface. We also discuss methods of handling cast shadows, which occur when one part of a face blocks the light from reaching another part of the face. Cast shadows have been treated by methods based on rendering a model to simulate shadows [18], whereas attached shadows can be accounted for with analytically derived linear subspaces.
Building truly accurate models of the way the face reflects light is a complex task. This is in part because skin is not homogeneous; light striking the face may be reflected by oils or water on the skin, by melanin in the epidermis, or by hemoglobin in the dermis, below the epidermis (see, for example, [2, 3, 33], which discuss these effects and build models of skin reflectance; see also Chap. 6). Based on empirical measurements of skin, Marschner et al. [32] state: “The BRDF itself is quite unusual; at small incidence angles it is almost Lambertian, but at higher angles strong forward scattering emerges.” Furthermore, light entering the skin at one point may scatter below the surface of the skin, and exit from another point. This phenomenon, known as subsurface scattering, cannot be modeled by a bidirectional reflectance function (BRDF), which assumes that light leaves a surface from the point that it strikes it. Jensen et al. [25] presented one model of subsurface scattering.
For purposes of realistic computer graphics, this complexity must be confronted in some way. For example, Borshukov and Lewis [11] reported that in The Matrix Reloaded, they began by modeling face reflectance using a Lambertian diffuse component and a modified Phong model to account for a Fresnel-like effect. “As production progressed, it became increasingly clear that realistic skin rendering couldn’t be achieved without subsurface scattering simulations.”
However, simpler models may be adequate for face recognition. They also lead to much simpler, more efficient algorithms. This suggests that even if one wishes to model face reflectance more accurately, simple models may provide useful, approximate algorithms that can initialize more complex ones. In this topic, we discussanalytically derived representation of the images produced by a convex, Lambertian object illuminated by distant light sources. We restrict ourselves to convex objects so we can ignore the effect of shadows cast by one part of the object on another part of it. We assume that the surface of the object reflects light according to Lambert’s law [30], which states that materials absorb light and reflect it uniformly in all directions. The only parameter of this model is the albedo at each point on the object, which describes the fraction of the light reflected at that point.
Specifically, according to Lambert’s law, if a light ray of intensity l coming from the direction Ul reaches a surface point with albedo ρ and normal direction vr, the intensity i reflected by the point due to this light is given by
If we fix the lighting and ignore ρ for now, the reflected light is a function of the surface normal alone. We write this function as τ(θΓ,φΓ), or r(vr). If light reaches a point from a multitude of directions, the light reflected by the point would be the integral over the contribution for each direction. If we denote k(u · v) = max(u · v, 0), we can write:
where jS2 denotes integration over the surface of the sphere.
PCA Based Linear Lighting Models
We can consider a face image as a point in a high-dimensional space by treating each pixel as a dimension. Then one can use PCA to determine how well one can approximate a set of face images using a low-dimensional, linear subspace. PCA was first applied to images of faces by Sirovitch and Kirby [44], and used for face recognition by Turk and Pentland [45]. Hallinan [19] used PCA to study the set of images that a single face in a fixed pose produces when illuminated by a floodlight placed in various positions. He found that a five- or six-dimensional subspace accurately models this set of images. Epstein et al. [14] and Yuille et al. [47] described experiments on a wide range of objects that indicate that images of Lambertian objects can be approximated by a linear subspace of between three and seven dimensions. Specifically, the set of images of a basketball were approximated to 94.4% by a 3D space and to 99.1% by a 7D space, whereas the images of a face were approximated to 90.2% by a 3D space and to 95.3% by a 7D space. This work suggests that lighting variation has a low-dimensional effect on face images, although it does not make clear the exact reasons for it.
Because of this low-dimensionality, linear representations based on PCA can be used to compensate for lighting variation. Georghiades et al. [18] used a 3D model of a face to render images with attached or with cast shadows. PCA is used to compress these images to a low-dimensional subspace, in which they are compared to new images (also using nonnegative lighting constraints we discuss in Sect. 7.5). One issue raised by this approach is that the linear subspace produced depends on the face’s pose. Computing this on-line, when pose is determined, is potentially expensive. Georghiades et al. [17] attacked this problem by sampling pose space and generating a linear subspace for each pose. Ishiyama and Sakamoto [21] instead generated a linear subspace in a model-based coordinate system, so this subspace can be transformed in 3D as the pose varies.
Linear Lighting Models without Shadows
The empirical study of the space occupied by the images of various real objects was to some degree motivated by a previous result that showed that Lambertian objects, in the absence of all shadows, produce a set of images that form a three-dimensional linear subspace [34, 40]. To see this, consider a Lambertian object illuminated by a point source described by the vector l. Let Pi denote a point on the object, let Ri be a unit vector describing the surface normal at Pi, let Pi denote the albedo at Pi, and define
In the absence of attached shadows, Lambertian reflectance is described by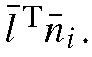
If we combine all of an object’s surface normals into a single matrix N, so the ith column of N is Ri, the entire image is described by
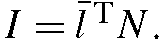This implies that any image is a linear combination of the three rows of N. These are three vectors consisting of the x, y, and z components of the object’s surface normals, scaled by albedo. Consequently, all images of an object lie in a threedimensional space spanned by these three vectors. Note that if we have multiple light sources,
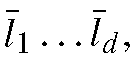we have
so this image, too, lies in this three-dimensional subspace. Belhumeur et al. [8] reported face recognition experiments using this 3D linear subspace. They found that this approach partially compensates for lighting variation, but not as well as methods that account for shadows.
Hayakawa [20] used factorization to build 3D models using this linear representation. Koenderink and van Doorn [28] augmented this space to account for an additional, perfect diffuse component. When in addition to a point source there is also an ambient light, I(Ul), which is constant as a function of direction, and we ignore cast shadows, it has the effect of adding the albedo at each point, scaled by a constant to the image. This leads to a set of images that occupy a four-dimensional linear subspace.
Nonlinear Models with Attached Shadows
Belhumeur and Kriegman [9] conducted an analytic study of the images an object produces when shadows are present. First, they pointed out that for arbitrary illumination, scene geometry, and reflectance properties, the set of images produced by an object forms a convex cone in image space. It is a cone because the intensity of lighting can be scaled by any positive value, creating an image scaled by the same positive value. It is convex because two lighting conditions that create two images can always be added together to produce a new lighting condition that creates an image that is the sum of the original two images. They call this set of images the illumination cone.
Then they showed that for a convex, Lambertian object in which there are attached shadows but no cast shadows the dimensionality of the illumination cone is O(n2) where n is the number of distinct surface normals visible on the object. For an object such as a sphere, in which every pixel is produced by a different surface normal, the illumination cone has volume in image space. This proves that the images of even a simple object do not lie in a low-dimensional linear subspace. They noted, however, that simulations indicate that the illumination cone is “thin”; that is, it lies near a low-dimensional image space, which is consistent with the experiments described in Sect. 7.3. They further showed how to construct the cone using the representation of Shashua [40]. Given three images obtained with lighting that produces no attached or cast shadows, they constructed a 3D linear representation, clipped all negative intensities at zero, and took convex combinations of the resulting images.
Georghiades and colleagues [17, 18] presented several algorithms that use the illumination cone for face recognition. The cone can be represented by sampling its extremal rays; this corresponds to rendering the face under a large number of point light sources. An image may be compared to a known face by measuring its distance to the illumination cone, which they showed can be computed using nonnegative least-squares algorithms. This is a convex optimization guaranteed to find a global minimum, but it is slow when applied to a high-dimensional image space. Therefore, they suggested running the algorithm after projecting the query image and the extremal rays to a lower-dimensional subspace using PCA.
Also of interest is the approach of Blicher and Roy [10], which buckets nearby surface normals, and renders a model based on the average intensity of image pixels that have been matched to normals within a bucket. This method assumes that similar normals produce similar intensities (after the intensity is divided by the albedo), so it is suitable for handling attached shadows. It is also extremely fast.
Spherical Harmonic Representations
The empirical evidence showing that for many common objects the illumination cone is “thin” even in the presence of attached shadows has remained unexplained until recently, when Basri and Jacobs [4, 6], and in parallel Ramamoorthi and Hanra-han [38], analyzed the illumination cone in terms of spherical harmonics. This analysis showed that, when we account for attached shadows, the images of a convex Lambertian object can be approximated to high accuracy using nine (or even fewer) basis images. In addition, this analysis provides explicit expressions for the basis images. These expressions can be used to construct efficient recognition algorithms that handle faces under arbitrary lighting. At the same time these expressions can be used to construct new shape reconstruction algorithms that work under unknown combinations of point and extended light sources. We next review this analysis. Our discussion is based primarily on the work of Basri and Jacobs [6].
Spherical Harmonics and the Funk-Hecke Theorem
The key to producing linear lighting models that account for attached shadows lies in noting that (7.2), which describes how lighting is transformed to reflectance, is analogous to a convolution on the surface of a sphere. For every surface normal vr, reflectance is determined by integrating the light coming from all directions weighted by the kernel k(ul · vr) = max(ul · vr, 0). For every vr this kernel is just a rotated version of the same function, which contains the positive portion of a cosine function. We denote the (unrotated) function k(ul) (defined by fixing vr at the north pole) and refer to it as the half-cosine function. Note that on the sphere convolution is well defined only when the kernel is rotationally symmetrical about the north pole, which indeed is the case for this kernel.
Just as the Fourier basis is convenient for examining the results of convolutions in the plane, similar tools exist for understanding the results of the analog of convolutions on the sphere. We now introduce these tools, and use them to show that when producing reflectance, k acts as a low-pass filter.
The surface spherical harmonics are a set of functions that form an orthonormal basis for the set of all functions on the surface of the sphere. We denote these functionsby Ynm, with n = 0, 1, 2,… and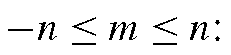
where Pnm represents the associated Legendre functions, defined as
We say that Ynm is an nth order harmonic.
It is sometimes convenient to parameterize Ynm as a function of space coordinates (x,y,z) rather than angles. The spherical harmonics, written Ynm(x,y,z), then be-come polynomials of degree n in (x,y,z). The first nine harmonics then become
where the superscripts e and o denote the even and odd components of the harmonics, respectively (so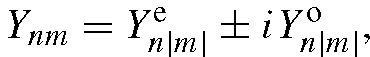
according to the sign of m; in fact
the even and odd versions of the harmonics are more convenient to use in practice because the reflectance function is real).
Because the spherical harmonics form an orthonormal basis, any piecewise continuous function, f, on the surface of the sphere can be written as a linear combination of an infinite series of harmonics. Specifically, for any f,
where fnm is a scalar value, computed as
and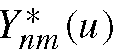
denotes the complex conjugate of
Rotating a function f results in a phase shift. Define for every n the n’th order amplitude of f as
Then rotating f does not change the amplitude of a particular order. It may shuffle values of the coefficients, fnm, for a particular order, but it does not shift energy between harmonics of different orders.
Both the lighting function, I, and the Lambertian kernel, k, can be written as sums of spherical harmonics. Denote by
the harmonic expansion of I, and by
Note that, because k(u) is circularly symmetrical about the north pole, only the zonal harmonics participate in this expansion, and
Spherical harmonics are useful for understanding the effect of convolution by k because of the Funk-Hecke theorem, which is analogous to the convolution theorem. Loosely speaking, the theorem states that we can expand I and k in terms of spherical harmonics, and then convolving them is equivalent to multiplication of the coefficients of this expansion (see Basri and Jacobs [6] for details).
Following the Funk-Hecke theorem, the harmonic expansion of the reflectance function, r , can be written as:
