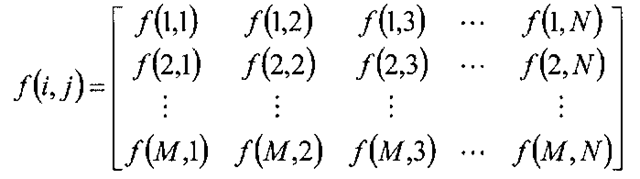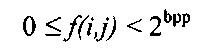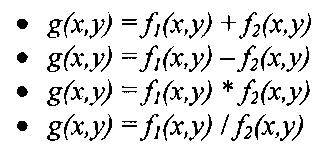When engineers or scientists refer to an image, they are typically speaking of an optical representation of a scene acquired using a device consisting of elements excited by some light source. When this scene is illuminated by a light source, these elements subsequently emit electrical signals that are digitized to form a set of "picture elements" or pixels. Together these pixels make up a digital image. Many of these devices are now driven by Digital Signal Processors, for reasons explained in 1.6. The imaging device may take the form of a camera, where a photographic image is created when the objects in the scene are illuminated by a natural light source such as the sun, or an artificial light source, such as a flash. Another example is an x-ray camera, in which case the "scene" is typically some portion of the human body or a dense object (e.g., luggage in an airport security system), with the light source consisting of x-ray beams. There are many other examples, some of which do not typically correspond to what most people think of as an image. For example, in the life sciences and biomedical fields there are numerous devices and instruments that can be thought of as cameras in some sense, where the acquisition detectors are photodiodes excited by some type of infrared light. This topic describes image processing algorithms that operate on all sorts of images, and provides numerous implementations of such algorithms targeting the Texas Instruments (TI) TMS320C6000™ DSP platform. Prior to embarking on this journey, this first topic introduces the structure of the topic and the representation of digital images, and the second topic provides background information on the tools used to develop image processing algorithms.
PREREQUISITES
In order to get the most out of this topic, it is expected that the reader is reasonably fluent in the C language and has had some exposure to MATLAB, C++, and the TI development environment. If the reader is completely new to embedded development on the TI DSP platform, but does have some experience using Microsoft Visual Studio or a similar integrated development environment (IDE), it should not be too difficult to pick up Code Composer Studio™ (CCStudio). CCStudio is heavily featured in this topic and is TI’s answer to Visual Studio. While one can always fall back to command-line compilation and makefiles, CCStudio incorporates many advanced features that make programming and debugging such a joy, as compared to the days of gdb, gcc, vi, and emacs.
One does not need to be an expert C++ programmer in order to make sense of the Visual Studio projects discussed in the topic. The use of C++ is purposely avoided on the DSP, however it is the language of choice for many programmers building scientific and engineering applications on Windows and UNIX workstations. For high-performance, non-embedded image processing, I would hasten to add that it is the only choice, perhaps leaving room for some assembly if need be. Nevertheless, I have eschewed many cutting-edge C++ features – about the most exotic C++ code one will encounter is the use of namespaces and perhaps a sprinkling of the Standard Template Library (STL). An understanding of what a class and method are, along with some C++ basics such as exception handling and the standard C++ library is all that is required, C++-wise.
The source code for all Visual Studio projects utilize Microsoft Foundation Classes (MFC) and GDI+ for their GUI components (see 2.4). For the most part, the layout of the code is structured such that one need not be a Windows programming guru in order to understand what is going on in these test applications. Those that are not interested in this aspect of development can ignore MFC and GDI+ and simply treat that portion of the software as a black box. Any in-depth reference information regarding Microsoft technologies can always be found in the Microsoft Developer’s Network (MSDN)3.
Lastly, a few words regarding mathematics, and specifically signal processing. In this topic, wherever image processing theory is presented, it is just enough so that the reader is not forced to delve into an algorithm without at least the basics in hand. Mainly this is due to space constraints, as the more theory that is covered, the fewer algorithms that can fit into a topic of this size. When it comes right down to it, in many respects image processing is essentially one-dimensional signal processing extended to two dimensions. In fact, it is often treated as an offshoot of one-dimensional signal processing. Unfortunately, there is not enough space to thoroughly cover the basics of one-dimensional DSP applications and so while some signal processing theory is covered, the reader will gain more from this topic if they have an understanding of basic signal processing topics such as convolution, sampling theory, and digital filtering. Texts covering such one-dimensional signal processing algorithms with applications to the same TI DSP development environments utilized in this topic include [4-6].
CONVENTIONS AND NOMENCLATURE
Many of the featured image processing algorithms are initially illustrated in pseudo-code form. The "language" used in the pseudo-code to describe the algorithms is not formal by any means, although it does resemble procedural languages like C/C++ or Pascal. For these pseudo-code listings, I have taken the liberty of loosely defining looping constructs and high-level assignment operators whose definitions should be self-explanatory from the context in which they appear. The pseudo-code also assumes zero-based indexing into arrays, a la C/C++.
Any reference to variables, functions, methods, or pathnames appear in a non-proportional Courier font, so that they stand out from the surrounding text. In various parts of the topic, code listings are given and these listings use a 10-point non-proportional font so they are highlighted from the rest of the text. This same font is used wherever any code snippets are needed. Cascading menu selections are denoted using the pipe symbol and a boldfaced font, for example File|Save is the "Save" option under the "File" main menu.
With any engineering discipline, there is unfortunately a propensity of acronyms, abbreviations, and terminology that may seem daunting at first. While in most cases the first instance of an acronym or abbreviation is accompanied by its full name, in lieu of a glossary the following is a list of common lingo and jargon the reader should be familiar with:
• C6x: refers to the TMS320C6000 family of DSPs, formally introduced in 2.1. The embedded image processing algorithms implemented in this topic target this family of DSPs. C6x is short-hand for the C62x, C67x, and C64x DSPs.
• IDE: integrated development environment. The burgeoning popularity of IDEs can be attributed in part to the success of Microsoft Visual Studio and earlier, Borland’s Turbo C and Turbo Pascal build systems. IDEs combine advanced source code editors, compilers, linkers, and debugging tools to form a complete build system. In this topic we utilize three IDEs (MATLAB, CCStudio, and Visual Studio), although MATLAB is somewhat different in that it is an interpreted language that does not require compilation or a separate linking step.
• TI: Texas Instruments, the makers of the C6x DSPs.
• CCStudio: abbreviation for the Code Composer Studio IDE, TI’s flagship development environment for their DSP products.
• M-file: a collection of MATLAB functions, analogous to a C/C++ module or source file.
• MEX-file: MATLAB callable C/C++ and FORTRAN programs.
• toolbox: add-on, application-specific solutions for MATLAB that contain a family of related M-files and possibly MEX-files. In this topic, the Image Processing Toolbox, Wavelet Toolbox, and Link for Code Composer Studio are all used. For further information on MATLAB toolboxes, see [7].
• host: refers to the PC where CCStudio is running. The host PC is connected to a TI DSP development board via USB, PCI, or parallel port.
• EVM: an abbreviation for evaluation module, introduced in 2.1.3. The EVM is a PCI board with a TI DSP and associated peripherals used to develop DSP applications. All EVM code in this topic was tested and debugged on an EVM containing a single C6701 DSP, and this product is referred to in the text as the C6701 EVM.
• DSK: refers to a "DSP starter kit", also introduced in 2.1.3. The DSK is an external board with a TI DSP and associated peripherals, connected to a host PC either via USB or parallel port (see Figure 2-4). All DSK code in this topic was tested and debugged on a DSK with a C6416 DSP, and this product is referred to in the text as the C6416 DSK.
• target: refers to the DSP development board, either an EVM or DSK.
Finally, a few words regarding the references to TI documentation – the amount of TI documentation is literally enormous, and unfortunately it is currently not located in its entirety in a central repository akin to MSDN. Each TI document has an associated "literature number", which accompanies each reference in this topic. The literature number is prefixed with a four-letter acronym – either SPRU for a user manual or SPRA for an application report. Some of these PDFs are included with the stock CCStudio install, but all of them can be downloaded from www.ti.com. For example, a reference to SPRU653.pdf (user manual 653) can be downloaded by entering "SPRU653" in the keyword search field on the TI web-site, if it is not already found within the docs\pdf subdirectory underneath the TI install directory (typically C:\TI).
THE REPRESENTATION OF DIGITAL IMAGES
Except for a single example in 3.4, this topic deals entirely with digital monochrome (black-and-white) images, oftentimes referred to as "intensity" images, or "gray-scale" images. A monochrome digital image can be thought of as a discretized two-dimensional function, where each point represents the light intensity at a particular spatial coordinate. These spatial coordinates are usually represented in a Cartesian system as a pair of positive integer values, typically denotes in this topic as (i,j) or (x,y). The spatial coordinate system favored in this topic is one where the first integer i or x is the row position and the second integer j or y is the column position, and the origin is the upper left corner of the image. Taken together, the discrete image function f(i,j) returns the pixel at the /’th row and /h column. Depending on the language, the tuples (i,j) or (x,y) may be zero-based (C/C++) or one-based (MATLAB) language. A digital image is usually represented as a matrix of values, and for example in MATLAB you have
The number of rows in the above image is M and the number of columns is N – these variable names show up repeatedly throughout the MATLAB code in this topic. In the C code, the preprocessor symbols X_SIZE and Y_SIZE refer to the number of rows and number of columns, respectively.
In the C and C++ languages, we represent an image as an array of two dimensions, and since both C and C++ use zero-based indices and brackets to specify a pointer dereference, the C/C++ equivalent to the above image matrix is
As explained in 3.2.2, for performance reasons we usually do not store images in the above fashion when coding image processing algorithms in C/C++. Very often, the image matrix is "flattened" and stored as a one-dimensional array. There are two prevalent ordering schemes for storing flattened 2D matrices, row-major and column-major. In row-major ordering, the matrix is stored as an array of rows, and this is the format used in C/C++ when defining 2D arrays. In the column-major format, which MATLAB and FORTRAN use, the matrix is ordered as an array of columns. Table 1-1 illustrates both of these formats, for the above example image matrix.
Table 1-1. Flattening an image matrix (with M columns and N rows) into a one-dimensional array
|
row-major |
column-major |
 |
 |
 |
 |
 |
 |
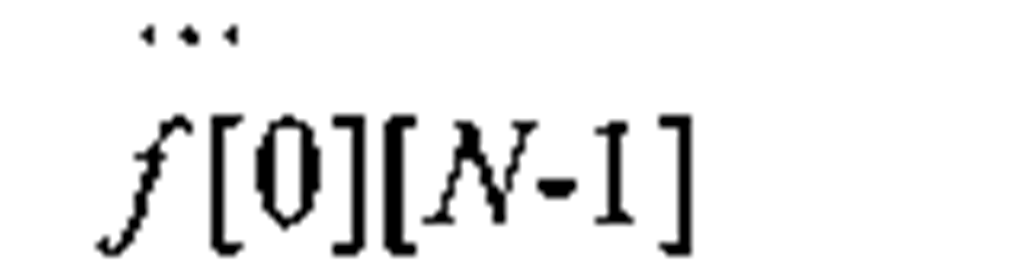 |
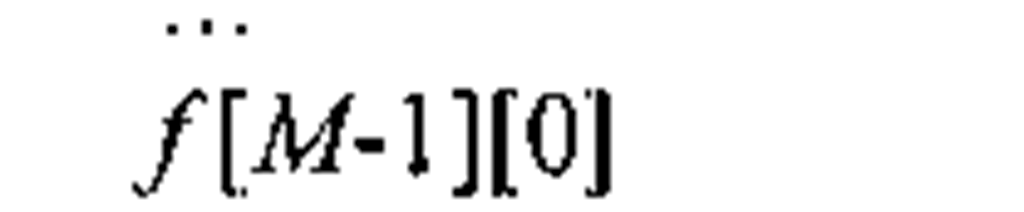 |
 |
 |
 |
 |
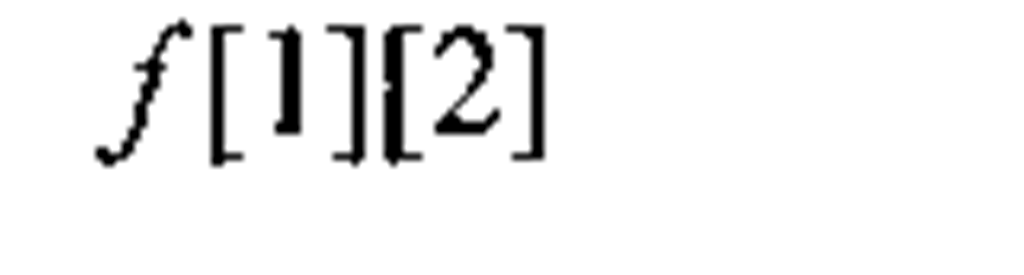 |
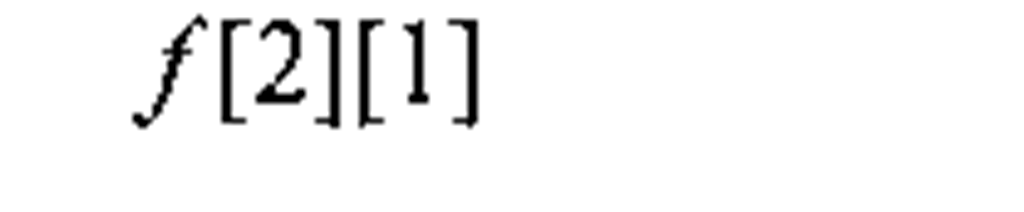 |
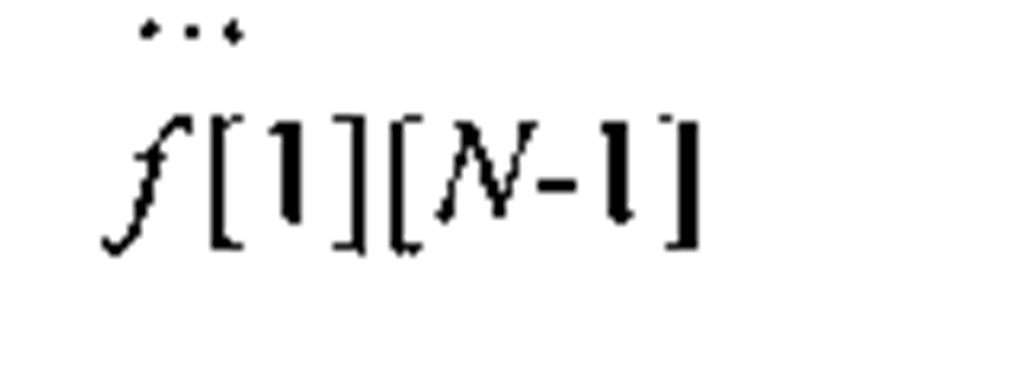 |
 |
 |
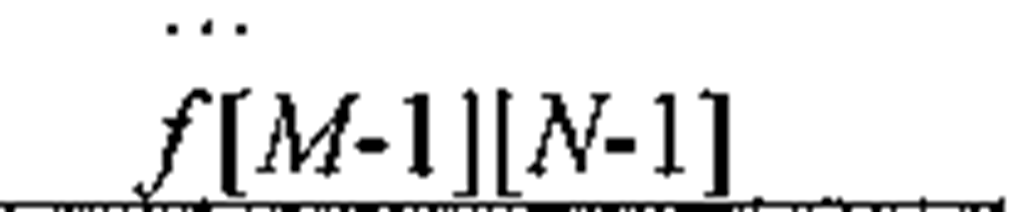 |
The individual pixels in digital monochrome images take on a finite range of values. Typically, the pixel values f(i,j) are such that
where "bpp" is bits-per-pixel. An individual pixel value f(i,j) goes by many commonly used names including: "gray-level intensity", "pixel intensity", or sometimes simply "pixel". In this topic, we largely deal with monochrome 8 bpp images, with pixel intensities ranging in value from 0 to 255. These types of images are sometimes referred to as 8-bit images.
DSP CHIPS AND IMAGE PROCESSING
For the most part, image processing algorithms are characterized by repetitively performing the same operation on a group of pixels. For example, some common arithmetic image operations involve a single image and a single scalar, as in the case of a scalar multiply:
The above expression translates in code to multiplying each pixel in the image/by the constant a. Bilinear operations are pixel-wise operations that assume images are of the same size, for example:
Another very common category of image processing algorithms are mask or filter operations, where each pixel f(x,y) is replaced by some function of f(x,yys neighboring pixels.Filtering a signal, either one-dimensional or multi-dimensional, involves repeated multiply-accumulate, or MAC, operations. The MAC operation takes three inputs, yields a single output, and is described as
As described in 2.1.2, in fixed-point architectures a, b, and c are integer values whereas with floating-point architectures those three are either single-precision or double-precision quantities. The MAC operation is of such importance that is has even yielded its own benchmark, the M-MAC, or million of multiply-accumulate operations per second (other benchmarks include MIPS, or million of instructions per second and MFLOPS, or million of floating-point instructions per second).
All of the above operations have one overriding characteristic that stands out among all others – they involve repetitive numerical computations requiring a high memory bandwidth. In short, image processing is both very compute- and data-intensive. In addition, image processing applications are increasingly finding themselves in embedded systems, oftentimes in settings where real-time deadlines must be met. With respect to embedded systems, consider the digital camera or camera cell phone. Such a device requires a computing brain that performs the numerical tasks described above highly efficiently, while at the same time minimizing power, memory use, and in the case of high-volume products, cost. Add to these real-time constraints, like the type one may encounter in surveillance systems or medical devices such as ultrasound or computer-aided surgery, and all of a sudden you now find yourself in a setting where it is very likely that a general purpose processor (GPP) is not the appropriate choice. GPPs are designed to perform a diverse range of computing tasks (many of them not numerically oriented) and typically run heavy-weight operating systems definitely not suited for embedded and especially real-time systems.
Digital Signal Processors arrived on the scene in the early 1980s to address the need to process continuous data streams in real-time. Initially they were largely used in ID signal processing applications like various telecommunication and audio applications, and today this largely remains the case. However, the rise of multimedia in the 1990s coincided with an increasing need to process images and video data streams, quite often in settings where a GPP was not going to be used. There has been a clear divergence in the evolution of DSPs and GPPs, although every manufacturer of GPPs, from Intel to SUN to AMD, has introduced DSP extensions to their processors. But the fact remains that by and large, DSP applications differ from their GPP counterparts in that they are most always characterized by relatively small programs (especially when compared to behemoths like databases, your typical web browser, or word processor) that entail intensive arithmetic processing, in particular the MAC operation that forms the building block of many a DSP algorithm. There is typically less logic involved in DSP programs, where logic refers to branching and control instructions. Rather, what you find is that DSP applications are dominated by tightly coded critical loops. DSPs are architected such that they maximize the performance of these critical loops, sometimes to the detriment of other more logic-oriented computing tasks. A DSP is thus the best choice for high-performance image processing, where the algorithms largely consist of repetitive numerical computations operating on pixels or groups of pixels, and where such processing must take place in a low-cost, low-power, embedded, and possibly real-time, system.
There are further unique architectural characteristics of DSPs that give them an edge in signal and image processing algorithms, including zero overhead loops, specialized I/O support, unique memory structures characterized by multiple memory banks and buses, saturated arithmetic, and others. In particular, there are certain vector operations that enable a huge boost in computational horsepower.The C64x DSP, discussed in the next topic, is particularly well suited for image processing applications as it is a high-speed DSP with numerous instructions that map very well to the efficient manipulation of 8-bit or 16bit pixels. For a more thorough discussion of DSP architectures and the history of the evolution of DSPs, the reader is referred to [9].
USEFUL INTERNET RESOURCES
There are a number of very useful web-sites pertaining to C6x development, and will leave the appropriate Internet search as an exercise for the reader. That being said, there is one resource above all others that anyone serious about C6x development should be aware of, and that is the Yahoo! group "c6x" (groups.yahoo.com/group/c6x/). This discussion forum is very active, and there are a few expert individuals who actively monitor the postings and are always giving their expert advice on a wide variety of topics pertaining to C6x DSP development.
In addition, the following USENET newsgroups are also important resources that should never be overlooked during an Internet search:
• comp.dsp: discussions on signal processing and some image processing applications, as well as general DSP development.
• comp.soft-sys.matlab: MATLAB-related programming.
• sci.image.processing: image processing algorithms.
The MathWorks also maintains the MATLAB Central File Exchange (www.mathworks.com/matlabcentral/fileexchange/), a very handy repository of user-contributed M-files. This site should be your first stop when searching for a particular MATLAB-based algorithm implementation. Finally, for Windows-related programming issues the following web-sites are highly recommended: www.codeproject.com and www.codeguru.com.