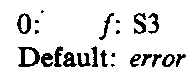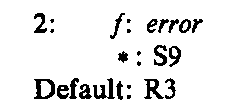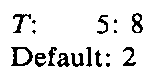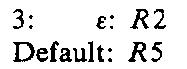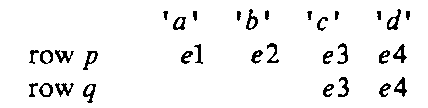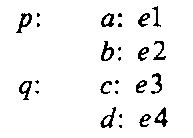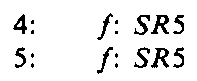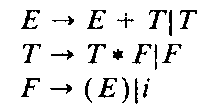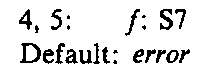Bottom-Up Parsing (Compiler Writing) Part 12

Representation and Optimization of LR Parsers

Thus far in this topic we have represented the F and G functions by two-dimensional matrices. Such representations are very efficient from a table-lookup standpoint. Since parsers for typical programming languages contain hundreds of states, the space requirements for storing the matrices can be very considerable. It has been shown (Purdom, 1974) that the number of states in a parser can be accurately estimated by the following formula:

where * = 0.5949 + 0.0048, y = 0.02 + 0.45, and C is the sum of all tokens in the right parts of all rules in the grammar plus the number of productions. Furthermore, the matrices tend to be sparse in the sense that many of their entries are blank (i.e., denote an error).

Two general approaches are used to reduce the size of the parsing tables. The first approach is to attempt to represent sparse matrices by suitable encodings. Several sparse-matrix encodings are possible. The second approach is to apply various transformations to the parsing tables. Some of these transformations can substantially reduce the number of states in the tables. The traditional state-minimization techniques that have been applied to finite-state machines cannot be applied to the parsing tables. This section examines both approaches with the aim of reducing space requirements for a parser.

There is a trade-off between the space taken by the parse tables on the one hand and the time taken to parse a given input string on the other. The matrix representation of the tables is expensive in storage requirements but fast in parsing time. A sparse-matrix (say, list) representation yields smaller tables, but usually at the expense of slower parsing times. In the past the designers of LR parsers have often chosen to reduce space requirements at the direct expense of compilation time. This choice is understandable in view of the large size requirements of early parsers and the high cost of main memory. Over the last decade, however, the cost of main memory has decreased substantially.

An important consideration in attempting to reduce the size of a parser is to preserve the same error-detection capabilities of an unreduced parser.

In this section we first examine sparse-matrix encodings and then present several space-saving transformations on the parsing tables.

Sparse-matrix representations. First, it is possible to combine the corresponding " terminal" columns of the F and G functions into "composite" columns. Such a reduction is based on the observation that if s is a state and a is a terminal symbol, the parsing-action entry in F is a shift operation if and only if the corresponding entry in G is not blank (Anderson et al., 1973; Aho and Ullman, 1973). For example, in Table 7-41, F(0,f) = Shift and G(0,f ) = 3. These two entries can be combined into a single ordered pair of the form  Shift 3 which indicates a shift and stack operation. All the next-state transition entries on terminals can be similarly represented as part of the F function, leaving the G table with only "nonterminal" columns. Using this approach, Table 7-41 can be represented as Table 7-43. The shift and reduce entries in the new representation can be encoded as positive and negative integers, respectively.

The blank entries in the next-state transition matrix are never used because errors are detected by the parsing-action table. The G table tends to be very sparse. Each column corresponding to a nonterminal symbol can be represented by a list. For example, the list for the column headed by T in Table 7-42 can be represented as follows:

Table 7-43 Encoded parsing tables for an LALR{ 1) grammar

State	/	—	+	*	c	S	£	T
0	S3					11	1	2
1		S4	SS
2		R3	R3	S9	R3
3		RS	RS	R5	R2
4	SI						6	2
5	S 7							8
6			SS		Rl
7		RS	R5	R5	R5
8		«4	R 4	S9	RA
9	510
10		R6	R 6	R 6	R6
11					A

 

where the list is identified by a nonterminal label and the first entry of an ordered pair is the row state number and the second the next-state transition value. The remaining nonterminal columns are represented as

The parse-action table can also be encoded in a similar manner but by rows instead of columns. It is convenient to introduce a default action, which specifies which entry applied when all others fail to match the current input symbol. The list representation of the first row of the action table becomes

As another example, the representation of the row labeled by state 2 becomes:

It is usually desirable to select as a default the most frequently occurring entry in the list. This selection reduces the size of the list. The default entry is always at the end of the list. The default approach can also be applied to representing the columns in the function G. The default list for the T column becomes

We can save more space in yet another way. Consider a state (i.e., a row) that contains only error and reduce entries. We can replace all the error entries with one of the reduce entries in that row. With this new representation, the parser may make more reductions than was the case with the original tables. In both cases, however, the error will be detected before the next input symbol is shifted. For example, the representation of the row associated with state 3 is

In general, any shift and accept entries should precede reduce entries in the list. The most frequently occurring reduce entry can be made a default action and all error entries can be ignored. The default action in a state that contains only shift entries is error.

Another way of compacting the parsing table is to take advantage of overlap between rows in the action table (F). For example, the two following rows:

indicate that the actions in row q are a suffix of those in row p. Row q can now be deleted by adding a label to part of row p as follows:

We next examine several transformations that optimize LR parsers.

Optimization transformations. Many transformations are possible that either reduce the space requirements of the parsing tables or decrease parsing time. Here we examine some of the most effective transformations. Some of the transformations depend on certain properties of the tables, while others take advantage of particular representations of these tables.

The subsection focuses on the following transformations:

1. LR(0) row elimination

2. Single-production elimination

3. Compatible state merger

These transformations all preserve the immediate error-detection property of LR parsers.

LR(0) row elimination Table 7-43 contains rows that have the LR(0) property. A row which has this property need not inspect the current input symbol in order to determine which action should be performed. For example, rows 7 and 10 have the LR(0) property. In each case a single reduce action is indicated. If we do not consult the current input symbol before performing a reduction, no significant delay in error detection will occur, since the left part of the rule which applies determines the next state. At some subsequent step the input symbol must be examined. We can eliminate rows that have a single reduce action by creating a new form of entry in the table that originally caused a transition to an LR(0) state. We denote this new form of entry a "shift-reduce" entry. As an example, row 7 can be detected by changing the entries for the parsing-action part of the table in the present example to the following:

where the entry SR 5 denotes a shift and reduce by production number 5 action.

Single-production elimination Many programming-language grammars contain productions of the formIn many instances these productions, called single productions, have no associated semantics. Therefore, the actions that recognize productions whose right-hand sides consist of single nonterminals are not necessary.

Productions of this form occur in most programming languages to define various kinds of expressions having a hierarchy (precedence levels) of operators. For example, the following grammar for arithmetic expressions contains such rules:

The two single productions areIn the parsing of the input string ‘/’ + /’, the reductions‘ must be performed on the first i. These reductions must be followed by the reductions on the second i. At this point the reduction E -* E + T can be performed. It is desirable to eliminate single productions having no semantic significance for two reasons. The parser resulting from this type of transformation is faster and in many cases more space-efficient.

Consider as an example the incompu parsing tables given in Table 7-44 in which the only reductions of the single production~ specified by the entries R,, occur in the row denoted by state p. Furthermore, assume that there is only one entry in the next-state transition table (G) which refers to state p. This entry appears in the column labeled by "the nonterminal B. Observe that the only way to reach state p is by the transition

Table 7-44 Example of a single-production elimination for the 1th production

Assume that after the parser performs the reductionin state p, it then consults the only next-state entry and then transfers to state q. The single reduction can be eliminated by changing the entry under column B from state p to state q. In this way we skip over the reduction and enter state q immediately. Since it was assumed that there was only one entry in the G table which referred to state p, this state becomes inaccessible. Therefore, row p can now be deleted from the tables. As a result, it is sometimes possible to merge nonterminal columns such as columns A and B in the example table.

The previous example illustrates a simple case that can arise. In general, there may be several states which indicate that reductions involving the same single productions are to be performed. Some methods (Anderson et al., 1973) can eliminate all single-production reductions from the tables, but sometimes at a cost of increasing the number of states because of state splitting in the parsing tables. Other methods (Aho and Ullman, 1973) eliminate most (but not all) of the single productions without increasing the size of the tables. Another method  eliminates all single productions and decreases the size of the tables. This method, however, is very complex. Yet another method (Lalonde, 1976) directly eliminates single productions at the initial table-construction phase.

Merging compatible states A straightforward optimization involves merging states with identical parsing actions. For example, rows 4 and 5 in Table 7-42 contain the same parsing action, the action "ST’. These two rows can be represented as

where the default action denotes an error entry. Recall that states 4 and 5 were already deleted because both were LR{0) states. In general, there may be several non-Li? (0) state rows which may be merged.

The preceding application of compatibility is very narrow, as both action rows must be identical. The notion of compatibility is as follows:

Two action rows are compatible if either their corresponding entries are identical, or one of them is an error entry.

Error detection is adversely affected by such a general definition.

Another approach (Aho and Ullman, 1972) to merging rows in the tables is to introduce the notion of don’t care entries in the tables. Some error entries in the parse-action entry (F) can never be referenced in parsing both valid and erroneous input strings. These don’t care entries can be overlaid as required to achieve compactness without significantly affecting error detection. The definition of compatibility used by Aho and Ullman is the following:

Two rows are compatible if either their corresponding entries are identical or one of them is a don’t care entry.

Most compatibility methods are complex. The methods, however, reduce storage requirements by at least a factor of 2.