Performance Parameters
In order to carry out effective performance calculations of the automobiles techniques have to be developed to cater for a number of performance parameters. The power delivered by the engine is finally made available at the drive wheels as propulsive force. The motion of a vehicle on a level road is resisted by air and rolling resistances. When tractive effort, the force available at the contact between driving wheels and road is more than the total resistance on level road, the surplus tractive effort contributes for acceleration, climbing gradients and draw-bar pull.
Calculation of equivalent weight, transmission efficiency, the position of centre of gravity, stability of a vehicle on a gradient and dynamics of a vehicle moving on banked track are also equally important for the evaluation of vehicle performance. This chapter discusses and lays down techniques to deal with these topics.
31.1.
Vehicle Drag
Vehicle drag is a force, which resists motion and is due to the deformation of the wheel and the ground (the later being negligible for vehicles on normal road) and the aerodynamic effects of air flow over the vehicle. The motion of vehicle for the straight-ahead position is considered, ignoring the effect of cornering for simplicity.
31.1.1.
Deformation of the Wheel
The pneumatic tyre is particularly suitable for use in road vehicles because of its contribution to comfort, its excellent adhesion properties and because it does not break up the road surface to the extent of a more rigid wheel. However, the vehicle load and tractive effect are not carried without deformation. In the case of a pneumatic tyre on the hard surface of a modern road, the deformation of the tyre accounts for 90 – 95% of the rolling resistance of a vehicle. The term rolling resistance is the drag force of the vehicle excluding that caused by aerodynamic effects. Windage and slippage losses are small in comparison. The distortion, of the tyre tread as it passes through the contact area results in a hysteresis loss, which manifests itself as heat and a rise in the temperature of the tyre.
The rolling resistance due to the hysteresis loss from the deformed tyre is primarily a function of tyre deflection, caused by the load carried by the tyre. Other parameters affecting the rolling resistance of a pneumatic tyre on a hard surface are tyre temperature, inflation pressure, vehicle speed, tread thickness, the number of piler, the mix of the rubber and the level of torque transmitted. The rolling resistance increases with vehicle speed if all other parameters are maintained constant. However, in practice, an increase in vehicle speed results in an increase in tyre temperature and pressure. The net result is, for a given tyre, a near constant rolling resistance with vehicle speed until such a speed is reached (Fig. 31.1) that a discernible standing wave sets in the tread in the wake of the contact area. The resistance to motion of the tyre increases very rapidly in this condition and the energy dissipated in the deformation caused by the standing wave is capable of destroying the tread in a very short time. It is usual, therefore, to specify a safe maximum speed for the particular tyre that is well below the speed at which the standing wave sets in.
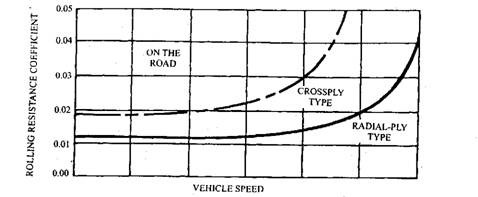
Fig. 31.1. Vehicle speed vs. rolling resistance.
Since there is direct relationship between load on a tyre, deflection and the hysteresis loss and since vehicle weight equates load on all the wheels, the rolling resistance, Rr, is expressed in terms of the non-dimensional rolling coefficient, a, as,
Rr = aW.
Since the rolling resistance cannot be taken as constant throughout the speed range of the vehicle, it is usual to add another coefficient, b, such that,
Rr = (a + b V)W, where V is the vehicle speed and W is the weight of the vehicle.
Vehicle performance calculations are usually conducted at the full throttle condition with high and fairly constant torque level through out the lower vehicle speed range where the rolling resistance is important. The rolling resistance coefficients used, therefore, should be at the appropriate torque level.
31.1.2.
Deformation of the Ground
Two cases are considered and both concern the operation of a vehicle on a surface other than hard road. In the first case the ground is considered ‘elastic’ so that the wheel of the vehicle deforms the ground, which then returns back to its original condition after the vehicle has passed. In the second case, the gound is considered ‘plastic’, where a permanent rut is left after the passage of the vehicle.
Figure 31.2 depicts the case of a rigid wheel on an elastic surface. The ground in front of the moving wheel in heaped up and flows from the front, under and around the wheel to the rear resulting in an energy loss and a rolling resistance. The effort of this on the wheel is to position the resultant, F, of the normal forces at some point A. The vertical component of the resultant force must equal the load, W, on the wheel (from equilibrium considerations) and the horizontal component constitutes the rolling resistance force. Taking moments about the centre ‘O’ of the wheel,
![]()
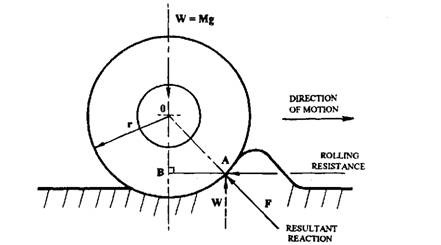
Fig. 31.2. Wheel on elastic ground.
If the ground is wholly plastic, an energy balance yields, giving
Rolling resistance = xpz
where, x is the width of the rut
p is the normal pressure between the wheel and the ground, and
z is the depth of sink-age.
In order to evaluate the above expression, it is necessary to know the normal pressure (p), which can be related to the sink-age (z) by,
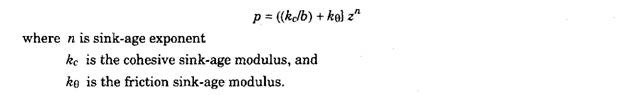
These three parameters are the properties of the soil. This expression has been developed for the case of a flat plate penetrating plastic ground, but is used for the case of the vehicle wheel also.
Using the relationship, vehicle weight = p x projected contact area under the wheels, both p and z and hence the rolling resistance can be found since the projected contact area under the wheel is a function of the sink-age, z.
The relationship between rolling resistance and vehicle weight is more complex and requires a detailed knowledge of the soil or ground material in the form of the three parameters n, kc and &e-
31.1.3.
Air Flow over the Vehicle
The moving vehicle, in displacing the surrounding air, has a resultant resisting force, called the aerodynamics drag (simply air resistance), and is imposed upon it. It is usual to express this drag non-dimensionally using the aerodynamic drag coefficient, Cd-
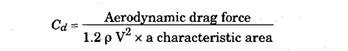
where p is air density, usually taken as 1.23 kg/m3 and Vis vehicle speed (m/s) relative to the air.
In order to nominate a suitable characteristic area, detailed study of the composition of the aerodynamic drag is necessary, which is due to three separate types of aerodynamic effects. (£) The air flow in the boundary layer resulting in the loss of momentum of the main
stream. This effect produces ‘skin friction’ drag. (ii) A component from the downstream of the trailing vortices behind the vehicle, resulting in the induced drag.
(Hi) The ‘normal pressure’ drag, which may be found by the integration of the product (normal pressure x area) around the vehicle. This produces a net force opposing the motion of the vehicle because the separation of flow at the rear of the vehicle results in a lowering of the pressure on the rearward facing surfaces.
The skin friction drag and the induced drag are usually small in comparison to the normal pressure drag. However, the skin friction drag can reach significant proportions in the case of a long vehicle, such as a coach. Since the major contributor to the aerodynamic drag is the normal pressure drag, the relevant characteristic area is the ‘projected frontal area’, A, of the vehicle.
A = 0.8 (vehicle height above ground level x body width)
However, such an approximate expression is no real substitute for a precise measurement and its use should be avoided. The aerodynamic drag coefficient, Cd, for a particular vehicle can be considered as constant if side wind effects are ignored.
