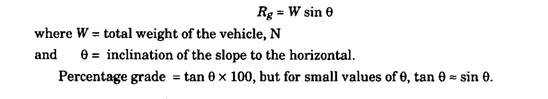31.2.
Power for Propulsion
The motion of a vehicle moving on a road is resisted by aerodynamic forces, known as wind or air resistance, and road resistance which is generally termed as rolling resistance. In addition to these two types of resistances, the vehicle has to overcome grade resistance when it moves up on a gradient, because the weight of the vehicle is to be lifted through a vertical distance. Hence, the power required to propel a vehicle is proportional to the total resistance to its motion and the speed.

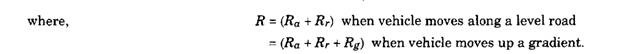
The calculation of engine power takes into account the losses in transmission. Hence required engine power,
![]()
31.2.1.
Air Resistance
This is the resistance offered by air to the movement of a vehicle. The air resistance has an influence on the performance, ride and stability of the vehicle and depends upon the size and shape of the body of the vehicle, its speed and the wind velocity. The last term should be taken into account when indicated, otherwise it can be neglected. Hence in general, air resistance,
Rolling Resistance
The magnitude of rolling resistance depends mainly on
(a) the nature of road surface,
(b) the types of tyre viz. pneumatic or solid rubber type,
(c) the weight of the vehicle, and
(d) the speed of the vehicle.
The rolling resistance is expressed as
![]()
where W = total weight of the vehicle, N
and K = constant of rolling resistance and depends on the nature of road surface and types of tyres = 0.0059 for good roads = 0.18 for loose sand roads = 0.015, a representative value. A more widely accepted expression for the rolling resistance is given by
![]()
where V = speed of the vehicle, km/hr.
Mean values of a and 6 are 0.015 and 0.00016 respectively.
31.2.3.
Grade Resistance
The component of the weight of the vehicle parallel to the gradient or the slope on which it moves is termed as ‘grade resistance’. Thus it depends upon the steepness of the grade. If the gradient is expressed as 1 in 5, it means that for every 5 metres the vehicle moves, it is lifted up by 1 metre. Hence, grade resistance is expressed as