28.4.
Brake Shoe and Pad Fundamentals
28.4.1.
Brake Shoe Self Energization
The drum type brake consists of two internal semicircular shoes, which are lined with friction material matching to the internal rubbing face of the drum. The shoes are fitted on a back plate, also known as a torque plate, between a pivot anchor or wedge type abutment at the lower shoe end and at the upper shoe top end by either a cam or hydraulic piston type expander. In Fig. 28.9 the expander is simply represented by two opposing arrows and the shoe linings by two small segmental blocks in the mid region of the shoes.
During clockwise rotation of the drum, the upper tips of the shoes are pushed apart by the expander force, Fe, and a normal inward reaction force, N, provided by the drum, resists any shoe expansion. Consequently the drum slid over the shoe linings and a tangential frictional force Ft = \iN is produced between each pair of rubbing surfaces.
The friction force or drag on the right hand shoe (Fig. 28.9) tends to move in the same direction as the shoe tip force Fe, which produces it. Accordingly this helps to drag the shoe onto the drum, so that the shoe tip force is raised effectively above that of the original expander force. This increase in shoe tip force above the input expander force is termed as positive servo, and shoes that provide this self-energizing or servo action are known as leading shoes.
![]()
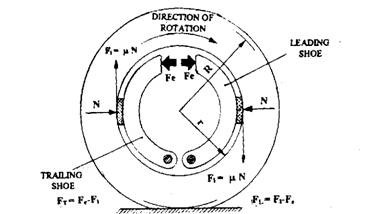
Fig. 28.9. Drum and shoe layout.
Likewise in the left hand shoe (Fig. 28.9), the frictional force or drag, Ft, tends to oppose the shoe tip force, Fe, so that the effective shoe tip force becomes less than the expander input force. This reduction in shoe tip force below that of the initial input tip force is termed as negative servo, and shoes, which provide this de-energizing action are known as trailing shoes.
Therefore, the trailing shoe tip resultant force, Ft = Fe~Ft
The magnitude of the self-energizing action greatly depends on the rubbing surface temperature, dampness, wetness, coefficient of friction and speed of drum rotation. Changing the direction of rotation of the drum causes the original leading and trailing shoes to become trailing and leading shoes respectively, so that their energizing characteristics are reversed. The shoe arrangement shown in Fig. 28.9 is termed as a leading-trailing shoe drum brake. Slightly more self-energizing is obtained if the shoe lining is heavily loaded at the outer ends as opposed to heavy mid-shoe loading.
28.4.2.
Retarding Wheel and Brake Drum Torques

Both these wheel and drum torques must be equal up to the point of wheel slip and they act in the opposite direction to each other.
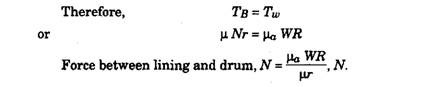
28.4.3.
Shoe and Brake Factors
If the brake is designed to produce a high braking force using a low effort, it has a high self-energizing or servo action. This desirable property is attained at the expensive of stability because any change in friction affects torque output disproportionately. A brake with little self-energization, requires a higher operating force compared to brake effort. This brake is more stable in operation and is less affected by frictional changes. The multiplication of effort or self-energizing characteristic for each shoe is known as the shoe factor.
The shoe factor, S, is defined as the ratio of the tangential drum drag, Ft, at the shoe periphery to the force, Fe, applied by the expander at the shoe tip.
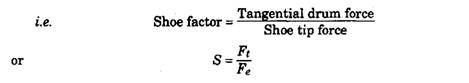
The combination of different shoe arrangements such as leading and trailing shoes, two leading shoes, two trailing shoes etc., produces a brake factor B that is the sum of the individual shoe factors.
Brake factor = Sum of shoe factors
![]()
28.4.4.
Theory of Internal Shoe Brake
Figure 28.10 represents an internal expanding shoe brake. With respect to the direction of rotation of drum the right hand side shoe is the leading shoe and the left-hand side the trailing one. The forces keeping them in equilibrium are shown in the figure except those acting at the pivot.
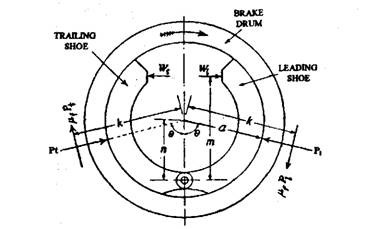
Fig. 28.10. Internal expanding shoe layout.
Wi and Wt are the actuating forces for leading and trailing shoes respectively. Pi and Pt are the normal forces between the shoe and the drum for leading and trailing shoes respectively arising due to actuating forces and act at an angle, 0, to the vertical. Pi and Pt produce frictional forces \ifPi and \ifPt respectively on the shoes. These forces act perpendicular to the normal forces and at a radius k called the effective radius. In practice the effective radius, k, is found to be greater than the drum radius, a. u/ stands for the coefficient of friction between the drum and shoe.
Considering leading shoe in equilibrium, the moments of all forces about the pivot give,

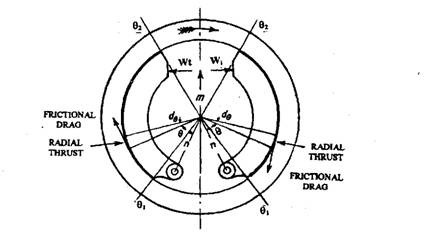
Fig. 28.11. Internal expanding shoes and drum.

The above equations are evaluated to get the required result after taking suitable assumption for the value of pi and pt. Two assumptions generally adopted are
(a) the intensity of pressure is constant over the surface of the lining; and (6) the shoe is rigid and the deformed lining is elastic in compression. This assumption gives that the intensity of pressure proportional to sin 0.
It should be noted that the magnitude of frictional torque on the drum depends upon the value of \if. The practical limit to the value of the \if is reached on the leading shoe when the moment of the frictional drag together with that of actuating force about the pivot becomes greater than due to the radial thrust. The shoe then locks to the drum, which is known as ‘sprag*.
Example 28.8. In a shoe-brake with leading and trailing shoes, the total actuating force of 471 N acts at a distance of 0.15 m from the pivot of the shoes which is 0.075 m from the axis of the drum of radius 0.09 m. The shoes have symmetrical lining with coefficient of friction 0.45. If the effective radius of the friction force is 0.1 m, calculate the total braking torque, when
(a) the actuating mechanism gives equal forces to the shoes;
(b) when the actuating mechanism gives the shoes equal displacement.
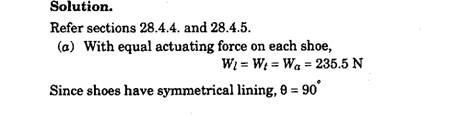

28.4.5.
Effect of Expanding Mechanism of Shoes on Total Braking Torque
In conventional brakes with internal shoes, two types of expanding mechanisms are applied. In one type the actuating forces on each shoe are equal. Hence,
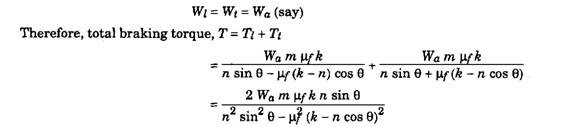
The second type of mechanism gives the shoes equal displacement and hence the actuating forces are in a fixed ratio. Equal displacements of shoes give the same rate of wear of brake linings. Further the rate of wear is proportional to energy dissipated by linings and energy dissipated is proportional to the product of brake shoe torque and the angular motion of the brake drum. The later being the same for both the shoes, the brake shoe torque must be equal.
One can find the actuating forces that would produce the same torque at leading and trailing shoes. Suppose equal actuating forces produce torques in the ratio TiITt, then for producing equal torque, the actuating forces must be in the ratio, TtlTi.
![]()
This can be expressed in words that for equal displacement of the shoes, the actuating forces Wt and Wi are in the inverse ratio of the brake torques obtained from the shoes with equal actuating forces.
28.4.6.
Calculation of Mean Lining Pressure and Heat Generation during Braking Operation
Figure 28.10 is referred for the forces acting between shoes and drum, and the following assumptions are made for simplifying calculations : (i) The linings are symmetrical.
(ii) Forces Pi and p. Pi act in the lining contact centre point of leading shoe. (Hi) Forces Pt and p. Pt act in the lining contact centre point of trailing shoe.
(iv) Forces Pt and Pi are equal.
(v) The value of u/is independent of pressure and velocity.

Now, if the speed of the vehicle is brought down from U km/hr to Vkm/hr in a distance of S meter, then retardation,


Example 28.9. A passenger car of all up-weight 14322.6 N is fitted with four wheel brakes and slowed uniformly from 86.5 km I hr to 48 km Ihrina distance of 152.5 m while running down an incline of 1 in 15. Calculate the mount of heat generated in kJ during this operation and mention the methods employed to transfer this heat to the atmosphere. If the front wheels share
55% of the braking forces, calculate the mean lining pressure in N/m2 on the front wheel brakes from the following data :
Brake lining width = 0.05 m
Effective wheel diameter = 0.686 m
Brake drum diameter = 0.318 m
Lining area per drum = 0.0321 m2
Coefficient of friction between drum and lining = 0.35 What is the lining contact angle is each drum ?


28.4.7.
Principle of the Disc Brake
The disc brake consists of a circular plate disc mounted on to and rotated by the wheel hub and a bridge member, termed as the caliper. The caliper straddles the disc and is attached to the suspension carrier, stub axle or axle casing (Fig. 28.12B). The caliper incorporates a pair of pistons and friction pads, which clamp the rotating disc during the application of the brakes. Consequently reduction of speed, proportional to the hydraulic pressure acting on each piston produced by the pedal effort, occurs.
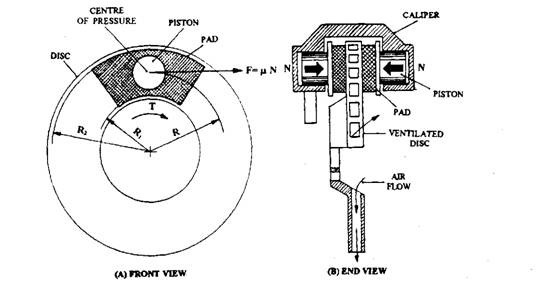
Fig. 28.12. Disc and pad layout.
The normal clamping thrust, N, on each side of the disc (Fig. 28.12B and C) produces a frictional force, F = \xN, at the interfaces of disc and pad on both sides of the disc. If the resultant frictional force acts through the centre of the friction pad then the mean distance between the centre of pad pressure and the centre of the disc becomes
![]()
where, i?i and R% are the inner and outer diameter of the pad respectively.
Accordingly, the frictional braking torque (Fig. 28.12A) is doubled due to the action of frictional force, N on both sides of the disc and depends upon the distance the pad is located from the disc centre of rotation.
![]()
Example 28.10. The distance between the pads centre of pressure and the centre of disc rotation is 0.12 and the coefficient of friction between the rubbing faces is 0.35. Determine the clamping force required to produce a braking torque of 82 Nm.
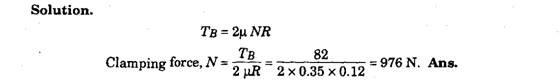
28.4.8.
Disc Brake Pad Alignment
During the application of brake, the pads are pressed against the disc with uniform pressure. However a slight tilt tendency exists between the leading and trailing pad edges due to frictional pad drag. Additionally the rate of wear from the inner to the outer pad edges is not uniform.
The thickness of the pad provides a small offset between the pad/disc interface and the pad’s back plate reaction abutment within the caliper (Fig. 28.12C). This produces a couple, which presses the pad harder against the disc at its leaning edge compared to the trailing edge. Consequently this effect causes a very small self-energizing servo action, due to which the wear rate at the leading edge is relatively higher than that at the trailing edge.
As the disc sweeps across the pad face, the circular distance it covers in one revolution increases proportionately from the inner to the outer edges of pad (Fig. 28.12A). Consequently the rubbing speed, and hence the work done increases from the inner to the outer edges, due to which the pad temperature and wear per unit area rises with the increase in the radial distance from the disc centre.
28.4.9.
A comparison of Shoe Factors and Shoe Stability
Different brake shoe arrangements and the disc brake are compared on a basis of shoe factor, S, or output torque against the variation df rubbing coefficient of friction (Fig. 28.13). The coefficient of friction, however, for most linings and pads ranges between 0.35 and 0.45. The shoe factor in increasing order is roughly as presented in Table 28.2 for the normal working range of the co-efficient of friction.
The figures in the table indicate that the torque output (shoe factor) for a single or two trailing shoes is only approximately one-third of the single or two leading shoe brake. The combination of a leading and trailing shoe performs at about twice that of the two trailing shoe, or roughly two-thirds of the two leading shoe layout (Fig. 28.13). The disc and pad perform a very similar to the two trailing shoe layout, but with higher coefficients of friction its shoe factor rises at a faster rate than that of the two trailing shoe brake. The duo servo shoe arrangement exhibits a superior shoe factor relative to all other layouts.
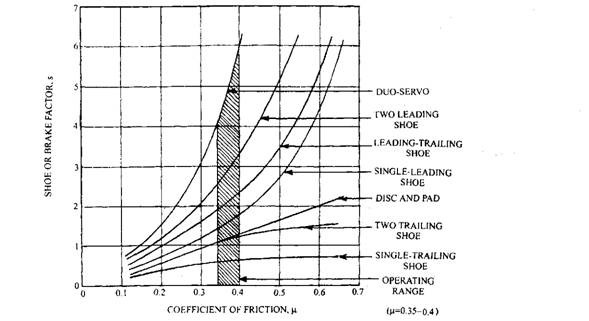
Fig. 28.13. Relationship of shoe or brake factors and coefficient of friction for different shoe layouts and the disc brake.
The lining or pad stability is the ability of the shoes or pads to maintain approximately the same shoe factor for a small change in the coefficient of friction, possibly because of wetness or an increase in temperature of the friction material. The stability changes in the reverse order as presented in Table 28.2. In general, brakes with very high shoe factors are unstable and produce a relatively large change in shoe factor (output torque) for a small increase or decrease in the coefficient of friction between the rubbing surfaces. Arrangements with low shoe factors tend to produce a consistent output torque for a considerable variation in the coefficient of friction. Since the shoe layouts with high shoe factors are unstable, the front brakes of most vehicles are either two leading shoes or disc and pads, and at the rear a leading and trailing shoe system. Additional assistance of vacuum or hydraulic servo or full power air operation is opted. A combined leading and trailing shoe brake thus provides a relatively high leading shoe factor but with only a moderate degree of stability, where as a trailing shoe produces a very low shoe factor with very high stability. Leading and trailing shoe brakes are still selected on the rear wheels because they easily accommodate the handbrake mechanism and produce an extra self-energizing effect when the handbrake is applied. Since this is not possible in the case of the disc and pad brake, it requires a considerably greater clamping force to achieve wheel lock condition.
Table 28.2. Shoe factor, relative braking power and stability for various brake layouts.
| Type of brake | Shoe factor | Relative braking power | Stability |
| Single trailing shoe | 0.55 | Very low | Very high |
| Two trailing shoes | 1.15 | Very low | Very high |
| Disc and pad | 1.2 | Low | High |
| Single leading shoe | 1.6 | High | Low |
| Leading and trailing shoes | 2.2 | Moderate | Moderate |
| Two leading shoes | 3.0 | High | Low |
| Duo servo shoes | 5.0 | Very high | Very low |
