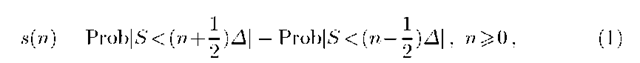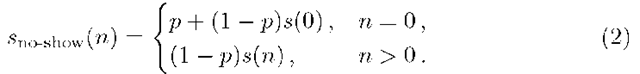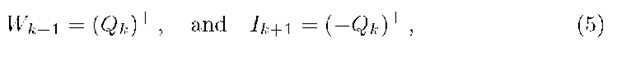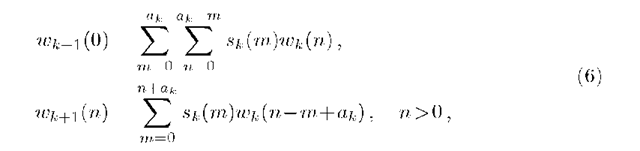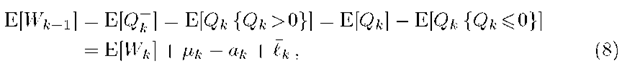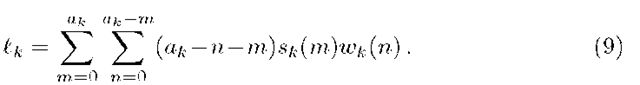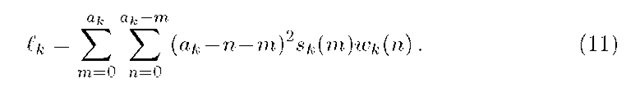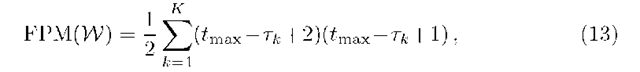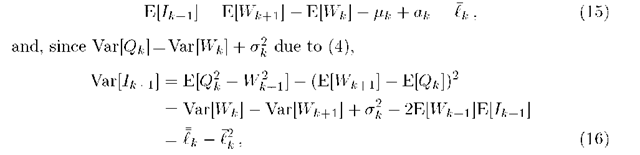Abstract
We consider the problem of evaluating an appointment schedule for outpatients in a hospital. Given a fixed-length session during which a physician sees K patients, each patient has to be given an appointment time during this session in advance. When a patient arrives on its appointment, the consultations of the previous patients are either already finished or are still going on, which respectively means that the physician has been standing idle or that the patient has to wait, both of which are undesirable. Optimising a schedule according to performance criteria such as patient waiting times, physician idle times, session overtime, etc. usually requires a heuristic search method involving a huge number of repeated schedule evaluations. Hence, the aim of our evaluation approach is to obtain accurate predictions as fast as possible, i.e. at a very low computational cost. This is achieved by (1) using Lindley’s recursion to allow for explicit expressions and (2) choosing a discrete-time (slotted) setting to make those expression easy to compute. We assume general, possibly distinct, distributions for the patient’s consultation times, which allows us to account for multiple treatment types, as well as patient no-shows. The moments of waiting and idle times are obtained. For each slot, we also calculate the moments of waiting and idle time of an additional patient, should it be appointed to that slot. As we demonstrate, a graphical representation of these quantities can be used to assist a sequential scheduling strategy, as often used in practice.
Introduction
Situation
Because of its social and economic interest, the question of how to schedule a hospital’s outpatients into the consultation session of a physician has received a lot of attention over the last sixty years. Many studies are motivated from a specific practical situation and aim at improving the organisational procedures in a particular (part of a) hospital [2,11,19,23]. Clearly, practical settings considerably differ in terms of medical practice, organisation, regulations, administrative demands or limitations, preferences of patients or medical staff, management issues, etc. However, very often the underlying problem is largely the same and can be formulated as follows. Consider the practice of a physician who consults patients during a time interval of a certain length called a session, for example a 4-hour session from 8am to 12am every week day. The physician is assisted by a nurse or secretary at the administration desk who is responsible for taking the calls of patients who wish to see the physician during the session of a particular day. The administrator must decide whether a calling patient can be admitted to that session and if so, at what time during the session the patient should arrive, i.e. what is his appointment time. All appointments are fixed before the session starts. The physician arrives at some point during the session, which is not necessarily the beginning. Given the session lengths and the number of patients, a ‘schedule’ consists of both the patient’s appointment times and the physician’s arrival time.
How a session evolves depends on its schedule. Since patients are consulted one by one in their appointed order, the patients in the waiting room behave as a FIFO (First-In First-Out) queueing system with the physician as service facility. The time required to serve a single patient is the consultation time, comprising all actions by the physician devoted only to that patient such as examination, looking up test results, giving advice, writing prescriptions, updating files, discussions, etc. It is clear that prior to the session, consultation times are known stochastically only and can be assumed independent. The arrival process on the other hand is not stochastic but consists of scheduled patient arrivals at deterministic time points. Hence, evaluating a session amounts to the study of a queueing system conditioned on a certain sample path for the arrivals. In fact, queueing systems with scheduled arrivals are known as appointment systems [12]. A patient arriving to the session at its appointed time can encounter two possible situations: either the physician has finished the consultations of previous patients or he has not. In the former case the physician has been without work, wasting time, since the departure of the last patient, whereas in the latter case it is the new patient who has to wait. As such, for each appointment there is either an idle time for the physician or a waiting time for the patient. As long as there is uncertainty on the consultation times when making the schedule it is impossible to avoid both idle and waiting times, although they can be controlled to a large extent by the schedule. Note that there is an ‘obvious’ trade-off. Scheduling appointments far apart results in low waiting times but long idle times and vice versa if the appointments are close together. The same consideration can be made at the end of the session: if the physician has finished all consultations before the end of the session, there is an undertime, whereas otherwise he has to work overtime. Again, session undertime and overtime are antagonistic and to some extent controllable by the schedule.
Modelling Issues
Depending on the specific situation, there are several so-called environmental factors that can make modelling the appointment systems considerably more complex, see [5] for an elaborate discussion. Patients may show up during the session that have no appointment (‘walk-ins’) but have to be seen by the physician anyway, either immediately (emergencies), in between regular patients or at the end of the session. Conversely, some patients that have an appointment do not show up for their consultation (‘no-shows’) or cancel the appointment too late. The no-show probability in some cases is up to 30%, depending on the type of health care offered and the patient population [10,15,21]. Clearly, walk-ins and no-shows contribute significantly to respectively the waiting and idle times of the schedule and to its overall uncertainty. Additionally, patients are not always punctual, for example arriving to the session later or sooner than they are supposed to. According to [1] the difference between appointed and actual arrival time is best modelled by an asymmetric Johnson distribution. Depending on the particularities of the used waiting-room policy, unpunctuality can result in overtaking of patients so that the original order of consultations is no longer maintained. With regard to scheduling, a complicating factor is also the fact that many patients have particular constraints concerning their appointment time. It is reported that as much as 25% of the calling patients [20] ask to be given an appointment in a certain subset of the session.
As to which distribution is suitable for modelling patient consultation times, several propositions have been made. Originally [4,3] Gamma distributions were used, also preferred in e.g. [7]. Other proposed distributions are Cox-type [22], lognormal [6], Weibull [2], uniform and/or exponential [12,13,14,17] and even deterministic consultations [10]. However, patients may also be considered heterogeneous, i.e. have different consultation time distributions. Unlike walk-ins and no-shows, heterogeneity can reduce schedule uncertainty if properly taken into account. For each calling patient, the administration can estimate the required consultation time distribution based on the person’s characteristics (age, medical record) and required type of medical treatment (medical scans, surgical procedures, inoculations, revalidation therapy, in-takes, discussion of test results, etc.).
Schedule Optimalisation
Constructing a schedule is targeted at striking an equitable trade-off between several performance criteria of the schedule such as waiting times of the subsequent patients, physician idle times, session overtime and undertime. Also, more subtle performance issues have been considered to be of importance, such as fairness (uniformity of patient waiting times), the number of patients seen in a session, the degree in which patient constraints can be met, etc. In general, it is not possible to construct the optimal schedule from the desired objective directly. Instead, a search method is required such as sequential quadratic programming [12], modified conjugate direction methods [22], stochastic linear programming [9] or local search methods [14]. These methods all basically work in the same way: take some initial schedule, evaluate it and based on its performance and the objective function try to improve it. Then do the same with the new schedule and so on until it is decided that no more significant improvements can be made. Unfortunately, only in some specific cases can convexity be proven, see e.g. [14]. In any case, since optimalisation requires a huge number of evaluations, it is very important to use an evaluation method that is both accurate and fast.
Concerning optimalisation however, a distinction needs to made between two possible ways of deciding the schedule. In many practical situations, sequential scheduling is employed where the schedule is built gradually over time, fixing the appointment for each patient immediately when they call in, until the session is full. With advance scheduling on the other hand, the appointment times are optimised for all patients at the same time, which is a much more complex task but can lead to better schedules.
Most studies impose certain limitations on the way appointments can be made and on how a session is organised, either to assure tractability of the evaluation method, reduce the search space or to make practical implementation easier. For example, often a session is be divided in blocks (possibly of different length) such that patients can only arrive at the start of a block, see e.g. [7,18,20]. Several scheduling ‘rules’ have been proposed to determine suitable appointment times for the patients, many of which are summarised in [5]. These rules differ e.g. in the prescribed number of patients in subsequent blocks, initial block size, the length of the intervals between the blocks (either fixed or variable), and so on. In [3] Bailey’s recommendation was to have the intervals be equal to the expected consultation time and let the physician start with the second patient. This is now known as ‘Bailey’s rule’ and was aimed at an equitable minimization of both patient waiting and physician idle times. More advanced rules exploit knowledge about patient heterogeneity, i.e. the fact that they have different known consultation time distributions. In [6] for example, a distinction is made between long and short consultations corresponding to ‘new’ and ‘return’ patients respectively. In [13] it is shown that it is beneficial to increase the intervals proportional to the standard deviation of each consultation time. Additionally, it is generally better to schedule consultations with low variance early in the session, see [20].
Discrete-Time Model and Assumptions
In this paper, we propose an analytic schedule evaluation method based on the recursive Lindley relation [16] in queueing theory. Our primary aim is to obtain expressions for the moments of the schedule’s performance criteria having very low computational complexity. Key to our approach is the discrete-time setting. That is, not only the session but also all time-related quantities in the model, such as waiting and idle times, are discretised into fixed-length intervals (slots) of length A. A suitable choice of A follows from a trade-off: whereas using small slots ensures a maximal accuracy of the performance predictions, choosing large slots results in a lower computational effort. In the envisaged medical context of appointments for outpatients, a practical time granularity is probably in the order of A = 1 minute, as it does not make sense to give people an appointment time with greater accuracy than this. More importantly however, any quantitative description of the consultation time of a patient or of a certain treatment type will rarely require a time granularity smaller than one minute. That is, in as far as the distribution of the anticipated consultation time S is not already made available as discrete data (a histogram), its distribution function can be quantised as
into the probability mass function (pmf) of a discrete random variable. Assuming that time is discrete simplifies the analysis considerably, since the integrals over finite intervals that follow from a continuous-time transient queueing analysis (see e.g. [7]) are replaced by finite sums. On the other hand, the discrete-time setting hardly compromises accuracy if the slot length A is chosen sufficiently small.
In our analysis, no assumptions are made on the consultation times of the patients other than that their pmf (1) is known and that they are independent. The fact that each patient can have a different consultation pmf allows us to evaluate schedules containing heterogeneous patients, which is important when making tight schedules with low cost. It is clear that the better the consultation time of a patient can be estimated beforehand, i.e. the smaller Var[S], the better the performance of the optimal schedule will be. For example, almost nothing can be assumed about a new patient seeing the physician for the first time, so a high-variance distribution of S must be assumed. For a patient only needing a prescription for a diagnosed chronic affliction however, the consultation time is almost deterministic. In appointment scheduling, there is much to be gained from a well-considered estimation of the anticipated consultation time of each particular patient. Therefore, the administrator is challenged to use as much advance knowledge about the patient as possible in order to maximally reduce the uncertainty on S. This can for example be done based on the patient’s medical history, on time measurements of previous consultations or simply by asking the patient some questions when he calls for an appointment.
We assume that all patients and the physician are punctual, arriving precisely when scheduled. Although patient lateness is excluded in our model, no-shows and even emergencies or other physician unavailabilities can be incorporated to some extent. Specifically, if a patient with consultation time pmf s(n) is likely not to show up for his appointment with probability p, his ‘effective’ consultation time has pmf
Likewise, if there is a probability q that a consultation with pmf s(n) will be interrupted by an emergency taking a length of time with pmf u(n), then the altered pmf is
where * denotes the discrete convolution. Finally, the physician doesn’t necessarily start seeing patients at the start of the session. To anticipate no-shows or lateness of the first few patients, the physician’s arrival may be scheduled later in the session.
Evaluation of an Appointment Schedule
Model Description
Consider a consultation session of a physician spanning a time period
in which K patients are given an appointment. Let Tk denote the appointment time of the kth patient
be the arrival time of the physician. All patients are assumed to be punctual and their consultation times constitute a sequence of independent random variables, denoted by
As already motivated, we assume time to be a discrete dimension where events can only happen at slot boundaries. Therefore, all time related measures are expressed as integer multiples of the slot length A. That is, the session length tmax, the physician arrival time 0 and the appointment times Tk are given as discrete values and the consultation times Sk have a discrete distribution with pmf
which may be obtained from (1) or otherwise available. We denote by
respectively the mean and variance of the kth patient’s consultation time.
A specific appointment schedule thus consists of the session length tmax, the physician arrival time 0, the number of patients K, their appointment times Tk and the consultation time distributions sk (n). Such a schedule can be evaluated in terms various criteria, among which the patient waiting time and the physician idle time are probably the most important. The waiting time Wk of the kth patient in the schedule is the time between its appointed arrival time and the effective start of its consultation. By the idle time Ik we mean the period before the arrival of patient k in which the physician has nothing to do because the consultation of patient k — 1 is already finished. Usually, for decision-making or optimalisation it is sufficient to predict the mean and the variance of these distributions, which can be calculated very efficiently as we demonstrate.
We denote the interarrival time between consecutive patients by
for k = 1, 2, …,K, where it is agreed that
indicates the end of the session. Hence, aK is the time between the last appointment and the end of the session. We can also interpret
as the arrival time of an additional virtual patient at the end of the session. This is useful, since the waiting time of this virtual patient equals the session overtime X, i.e. the excess time beyond the scheduled end of the session that the physician requires to see all K patients. Clearly, the overtime X = WK+1 is an important criterium for the performance of the schedule as well.
Analysis
If we define the auxiliary variable
for k = 1,… ,K, then the well-known Lindley equation in queueing theory [16] relates the waiting and idle times of consecutive patients as
where (•)+ is a shorthand notation for max(0). Note that Wk+1 and Ik+1 cannot both be positive at the same time, although Wk+1 = Ik+1 = Qk =0 may occur when the consultation of patient k finishes exactly in the slot before the arrival of patient k +1. For further calculations, we distinguish between the case Qk = -Ik+1 ^ 0 where patient k +1 can be seen immediately and the case Qk = Wk+1 > 0 where this patient has to wait. In particular, the probability mass function wk+1 (n) = Prob[Wk+1 = n], n ^ 0 of the (k +1)th waiting time can be related to that of the previous patient using (5). We find
where we exploited the fact that the waiting time of a patient and his consultation time are independent. These probabilities are easy to calculate due to the discrete-time modelling. The first patient is scheduled either before or after the physician’s arrival, and has deterministic waiting and idle times respectively given by
Hence, the pmf w1 (n) is immediately given and the relations (6) allow us to calculate wk (n) recursively for all n and k, as far as necessary.
In principle, if the consultation times are bounded, it is possible to calculate the complete probability mass function of the waiting times from which moments can be determined. Such an approach however, is computationally demanding and not applicable if consultation times have unbounded support. Nevertheless, calculation of the probabilities (6) can be partially avoided as long as only the moments of waiting and idle times are required. For example, again by (4)-(5), the mean waiting times of subsequently scheduled patients are related as
for k =1,.. .,K and where £k is the finite sum,
In a similar way, we obtain for the waiting time variances
with
Again, because of (7) we have that
respectively, such that by (6)-(11) the mean and variance of the waiting times of the patients can be determined recursively for k = 2,…,K. It is now also clear that only a finite number of waiting time probabilities need to be calculated by means of (6), even though the consultation times Sk may be stochastically unbounded. Specifically, in accordance with (8)-(9), the calculation of 
requires probabilities
which in turn requires
and so on, until finally for the first patient we need
Note that because W1 is deterministic, all probabilities in the latter range are zero, except for one. For the variances of the patient waiting times, the same finite set of probabilities
is used. This set W is computationally the most demanding part of the schedule’s evaluation, in terms of the required number of floating-point multiplications, given by
in the worst case where the consultation times have infinite support. For a session of length tmax with K patients scheduled at equal distances, FPM(W) is
The moments of the physician idle times that occur before each patient’s appointment are related to the moments of the waiting times by means of
a direct consequence of (5). Hence, for k =1, …,K one finds
which are all known quantities at this point. Recall that X = Wk+i is the session overtime of which mean and variance follows from the algorithm explained above. In the same way, the idle time IK+1 associated with the virtual patient at the end of the session can be interpreted as the session undertime, i.e. the time by which the physician finishes the session early after seeing all K patients.
Examples
In the following examples, we evaluate some particular schedules with regard to the incurred mean waiting, idle and overtime. We assume a slot length of A =1 minute. If
denotes the (continuous) ^-distribution with mean p and variance
then we refer to the corresponding discrete distribution obtained by (1) as
Fig. 1. Evaluation of a schedule with K = 10 patients equidistantly spaced in a session of length tmax = 200, 240 and 280 minutes. All patients have the same -T(20, 50) consultation time distribution with the pmf shown in (a). The physician starts 6 = 5 minutes after the session starts.
First, we consider a session with K = 10 patients all having the same consultation time distribution r(20, 50) of which the pmf is shown in Fig. 1(a). The patients are given appointment times equidistantly spaced in the session, i.e.
while the physician arrives 5 minutes late in the session. The mean performance of this schedule is shown in Fig. 1(b), (c) and (d) in case the spacing a is 20, 24 and 28 minutes respectively. Note that in (b) the time given to each patient is exactly the expected time needed by the patient, i.e.
Although one would expect this to be an acceptable strategy, it is clearly not since the waiting times of subsequently scheduled patients increase indefinitely (assuming an infinite session
kept constant), as already observed in [4]. For long sessions it is therefore necessary to choose a larger spacing, for example as
with some parameter h>0 [8]. Taking the spacing a too large however, as in (d), results in very high physician idle times.
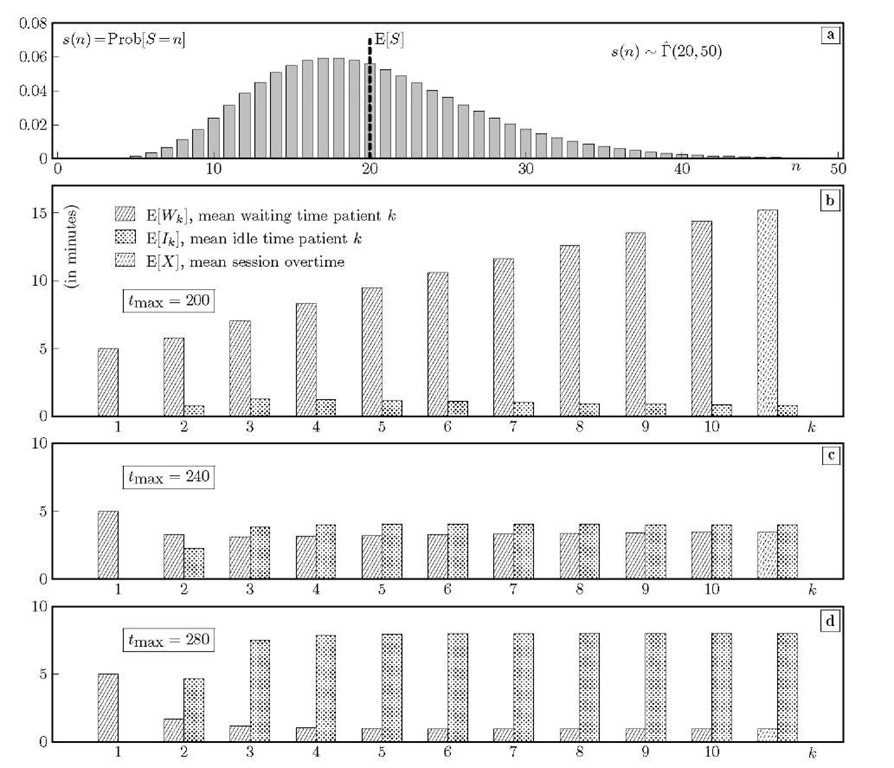
Fig. 2. Schedule with tmax = 240, 6 = 5 and K = 10 equidistant patients. Compared to Fig. 1(c), the variance of the consultation times is increased to 100 in (a)-(b) and to 200 in (c)-(d).
In Fig. 2 we illustrate the influence of consultation time variability in another way. We consider again the schedule of Fig. 1(c) where the patients are placed every 24 minutes but now increase the variance a of the consultation times from a = 50 to a = 100 and 200 in Fig. 2(a)-(b) and (c)-(d) respectively, keeping the mean consultation time at 20 minutes. Observe that a high-variance consultation time attributes more uncertainty to the schedule and deteriorates both the mean waiting times and idle times [3,5,13,20]. Moreover, the mean waiting times of subsequent patients in Fig. 2(d) increase towards the end of the session, similar as in Fig. 1(b). Here however, if the session were infinite, the waiting times would converge to a limiting value since ak < lk. 
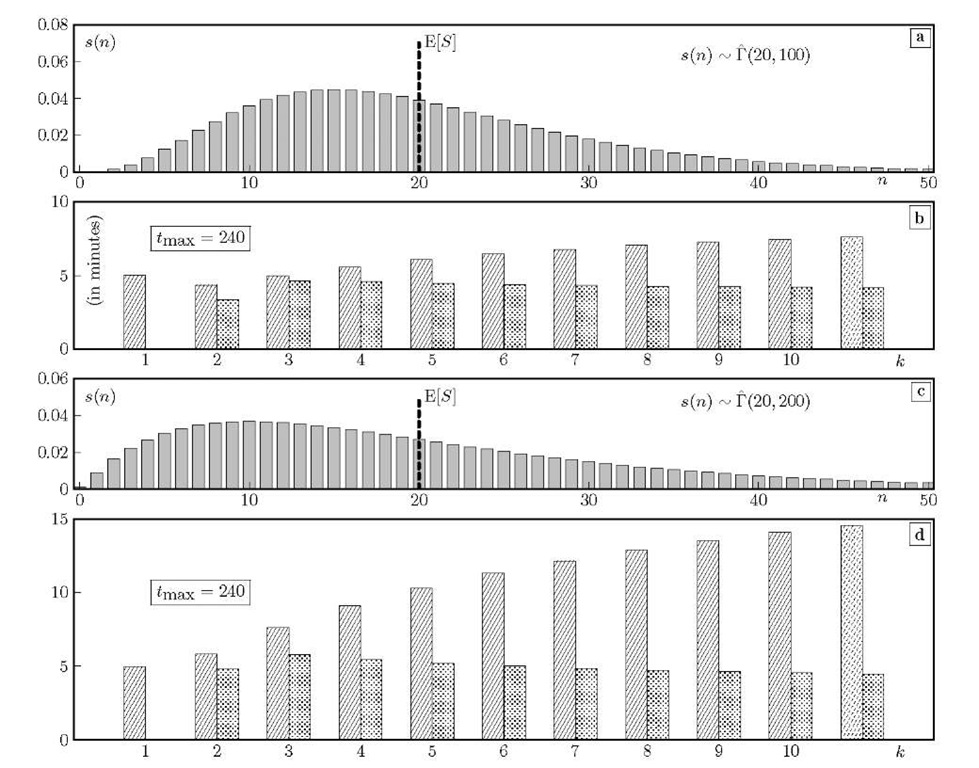
Fig. 3. Schedule with
equidistant patients. Starting from a /(20,150) consultation time pmf s(n), we show the effect of adjusting for a no-show probability of 15%. In (a)-(b), the probabilities s(n) are simply rescaled, while in (c)-(d) the shape and scale parameter of the Gamma distribution are adjusted to yield the same mean and variance as for s(n).
In Fig. 3 we illustrate the consequence of no-shows on the schedule’s performance, again assuming tmax = 240, 0 = 5 and K =10 equally spaced patients, i.e. every ak = 24 minutes. The consultation times are all /(20,150) distributed. In (a) we show the effective pmf s*(n) obtained from rescaling s(n) as in (2) in order to account for a no-show probability p of 15%. Note that the probability mass s*(n) = 0.15 of a zero-length consultation is not shown completely. In (b) the schedule’s performance is shown both in the original case where all patients show up and in case the rescaled pmf s* (n) is used. As the mean consultation time drops from E[S] = pk = 20 to E[S*] = p*k = 17 minutes due to the no-shows, the waiting times are lower while the idle times are higher.
In Fig. 3(c)-(d) we illustrate that the consultation time distribution may have an influence beyond its first two moments, due to the sums (9) and (11). Here, both S and S* have their mean and variance equal to 20 and 150 respectively, although only S is /"-distributed. The second distribution is obtained by imposing a no-show probability s* (0) = p = 15% and choosing a /"-shape for the other mass points s*(n), n>0.
