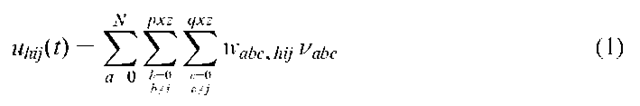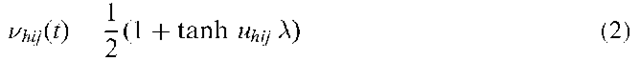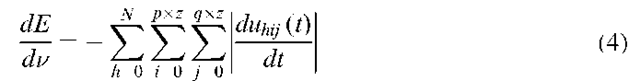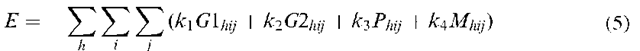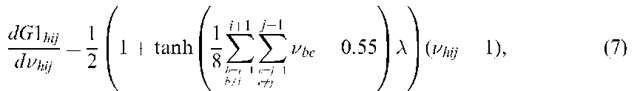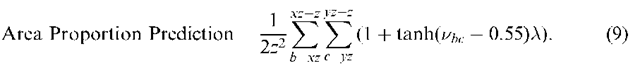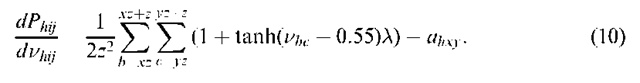Introduction
Accurate information on land cover is required to aid the understanding and management of the environment. Land cover represents a critical biophysical variable in determining the functioning of terrestrial ecosystems in bio-geochemical cycling, hydrological processes and the interaction between surface and atmosphere (Cihlar et al., 2000). Information on land cover is central to all scientific studies that aim to understand terrestrial dynamics and is required from local to global scales to aid planning, while safeguarding environmental concerns. It is, therefore, central to all scientific studies that aim to understand terrestrial dynamics at any scale. In addition to this, the identification, extraction and mapping of target land cover features with low levels of uncertainty is vital in many areas of land management. Such information has many uses including those related to inventories of land resources, monitoring environmental change, and predicting future environmental scenarios.
Digital remotely sensed imagery derived from aircraft and satellite mounted sensors can provide the information required for land cover mapping and, since the 1970s, automated techniques for thematic map production have been used widely. The dominant approach, still used widely today, is hard classification (Campbell, 1996).
In a hard classification, land cover is represented as a series of discrete units, whereby each pixel is associated with a single land cover class. Among the most frequently used hard classification algorithms are the parallelepiped, minimum distance and maximum likelihood decision rules (Campbell, 1996). However, there exist practical limitations with the single class per-pixel assumption underlying hard classification.
The use of a hard classifier corresponds to the partitioning of feature space into mutually exclusive decision regions. These algorithms ignore the fact that many pixels in a remotely sensed image represent an average of spectral signatures from two or more surface categories. For example, a Landsat Thematic Mapper (TM) image (with a spatial resolution of 30 m by 30 m (120 m by 120 m in band 6)) of an urban scene may contain many pixels that represent more than one land cover class. Even in rural areas a Landsat TM scene may contain mixed pixels at the boundaries between land cover types, for example, between agricultural fields. This mixing of signatures occurs as a function of:
(i) Frequency of land cover - the physical continuum that exists in many cases between discrete category labels, combined with the spatially mixed nature of most natural land cover classes.
(ii) Frequency of sampling - the spatial integration within the pixel of land cover classes due to factors such as the sensor spatial resolution, point spread function (PSF) and resampling for geometric rectification.
The mixed pixel problem affects data acquired by satellite sensors of all spatial resolutions. Distinguishing the sources of mixing within an image is only possible in controlled and limited situations (Schowengerdt, 1996) meaning that classifications produced via hard classification may contain much uncertainty.
The problems above prompted the development and usage of classifiers that attempt to reduce error and uncertainty by accounting for mixed pixels. A hard classification fails to recognize or represent the existence of classes and objects which grade into one another and class boundaries at sub-pixel scales, leaving the classification user uncertain of the accuracy of the prediction. Such simplification can be seen as a waste of the available multispectral information, which could be interpreted more efficiently.Therefore, since an initial approach by Horowitz et al. (1971), many studies have used various techniques to attempt to ‘unmix’ the information from pixels. Typically, these produce a set of images, one for each land cover class, in which each pixel has a membership value between 0 and 1 to the relevant class.In general, two different types of soft classification technique exist. The most commonly used methods predict posterior probabilities of class membership using statistical pattern recognition methods, and correlate these with area proportions. However, as Lewis et al. (1999) state, posterior probabilities are measures of statistical uncertainty, and there is no causal relationship with proportions of pixels containing the class, despite their correlation. Thus, as a consequence, posterior probabilities cannot represent optimum predictions of area (Manslow and Nixon, 2000). The second type of soft classification technique predicts directly class area proportions using regression models. Lewis et al. (1999) demonstrate that posterior probabilities do not represent optimum area predictions, and direct area proportion models achieve more accurate predictions of true land cover proportions.
Soft classification involves the prediction of sub-pixel class composition through the use of techniques such as spectral mixture modelling (Garcia-Haro et al., 1996), multi-layer perceptrons,nearest neighbour classifiers (Scho-wengerdt, 1997) and support vector machines (Brown et al., 1999). The output of these techniques generally takes the form of a set of proportion images, each displaying the proportion of a certain class within each pixel. In most cases, this results in a more appropriate and informative representation of land cover than that produced using a hard, one class per-pixel classification. However, while the class composition of every pixel is predicted, the spatial distribution of these class components within the pixel remains unknown. Therefore, while soft classification conveys more information than hard classification, the resultant predictions still contain a large degree of uncertainty.
The overview below of work previously undertaken by the authors of this topic, along with other work in the literature, demonstrates that it is possible to map land cover at the sub-pixel scale, thus, reducing the uncertainty inherent in maps produced solely by hard or soft classification.
Previous Image Mapping at the Sub-pixel Scale
Previous work on mapping or reconstructing images at the sub-pixel scale to reduce uncertainty has taken the form of three differing approaches, namely (i) image fusion and sharpening, (ii) image reconstruction and restoration and (iii) super-resolution.
Image fusion and sharpening
The basis for image fusion and sharpening stems from the fact that there will always be some trade-off within the field of remote sensing between spatial and spectral resolution. Images with fine spatial resolution can be used to locate objects accurately, whereas images with fine spectral resolution can be used to identify and quantify variables accurately. With different sensors acquiring information over the same area, it is often useful to merge the data into a hybrid product containing the useful information from each. Such a hybrid image can be used to create detailed ‘sharpened’ images that map the abundance of various materials within a scene. Therefore, image fusion techniques may be used to merge images of different spatial and spectral resolutions to create a fine spatial resolution multi-spectral combination (Gross and Schott, 1998).
Generally, two approaches to fusion and sharpening exist. The first uses a two-step approach whereby, firstly, the coarse spatial resolution multi-spectral image is used to identify the materials in the scene via soft classification. Second, the proportion maps are combined with a fine spatial resolution panchromatic image of the same area, which serves to constrain the proportions to produce a set of ‘sharpened’ fine spatial resolution maps. This has been carried out for synthetic images (Gross and Schott, 1998), agricultural fields (Li et al., 1998) and for a lake,used a finer spatial resolution image and a simple regression based approach to sharpen the output of a soft classification of a coarser spatial resolution image, producing a sub-pixel land cover map. The results produced a visually realistic representation of the lake being studied, and this was further refined by fitting class membership contours, lessening the blocky nature of the representation. However, the areal extent of the lake was not maintained, and generally, obtaining two coincident images of differing spatial resolution is difficult.
The second approach to fusion and sharpening should conceptually produce identical results. Image fusion is undertaken to produce a fine spatial resolution multi-spectral image that is then unmixed into fine spatial resolution material maps. There is little published work of this approach, although Robinson et al. (2000) used it with synthetic imagery.
Image reconstruction and restoration
Digital image reconstruction refers to the process of predicting a continuous image from its samples and has fundamental importance in digital image processing, particularly in applications requiring image resampling. Its role in such applications is to provide a spatial continuum of image values from discrete pixels so that the input image may be resampled at any arbitrary position, even those at which no data were originally supplied (Boult and Wolberg, 1993).
Whereas reconstruction simply derives a continuous image from its samples, restoration attempts to go one step further. It assumes that the underlying image has undergone some degradation before sampling, and so attempts to predict the original continuous image from its corrupted samples. Restoration techniques must, therefore, model the degradation and invert its effects on the observed image samples, a process which itself contains a large degree of uncertainty when dealing with satellite sensor imagery.
Super-resolution
Super-resolution techniques are similar to the reconstruction and restoration approaches in that they predict image values at points where no data were originally supplied. However, where the reconstruction and restoration techniques attempt the difficult and uncertain task of recovering a continuous image, the super-resolution approaches merely attempt to increase the spatial resolution of an image to a desired level. This solves the problem of the computational complexity associated with the reconstruction and restoration techniques, making the super-resolution techniques applicable to remotely sensed data.Various differing approaches to super-resolution mapping have been attempted.
Schneider (1993) introduced a knowledge-based analysis technique for the automatic localization of field boundaries with sub-pixel accuracy. The technique relies on knowledge of straight boundary features within Landsat TM scenes, and serves as a pre-processing step prior to automatic pixel-by-pixel land cover classification. With knowledge of pure pixel values either side of a boundary, a model can be defined for each 3 by 3 block of pixels. The model uses variables such as pure pixel values, boundary angle, and distance of boundary from the centre pixel. Using least squares adjustment, the most appropriate model parameters are chosen for location of a sub-pixel boundary, dividing mixed pixels into their respective pure components. Improvements on this technique were described by Steinwendner and Schneider (1997), who used a neural network to speed up processing. In addition Steinwendner and Schneider (1998), Steinwendner et al. (1998) and Steinwendner (1999) suggested algorithmic improvements, along with the addition of a vector segmentation step. The technique represents a successful, automated and simplistic pre-processing step for increasing the spatial resolution of satellite sensor imagery. However, its application is limited to imagery containing large features with straight boundaries at a certain spatial resolution, and the models used still have problems resolving image pixels containing more than two classes (Schneider, 1999).
Flack et al. (1994) concentrated on sub-pixel mapping at the borders of agricultural fields, where pixels of mixed class composition occur. Edge detection and segmentation techniques were used to identify field boundaries and the Hough transform (Leavers, 1993) was applied to identify the straight, sub-pixel boundaries. These vector boundaries were superimposed on a sub-sampled version of the image, and the mixed pixels were reassigned each side of the boundaries. By altering the image sub-sampling, the degree to which the spatial resolution was increased could be controlled. No validation was carried out, and the work was not followed up, and so the appropriateness of the technique remains unclear.
Aplin (1999, 2000) made use of sub-pixel scale vector boundary information, along with fine spatial resolution satellite sensor imagery to map land cover. By utilizing Ordnance Survey land line vector data fused with CASI imagery, and undertaking per-field rather than the traditional per-pixel land cover classification, mapping at a sub-pixel scale was demonstrated. Assessments suggested that the per-field classification technique was generally more accurate than the per-pixel classification (Aplin et al., 1999). However, in most cases, availability of accurate vector data sets to apply the approach will be rare, and the technique is limited to features large enough to appear on such data sets.
The three techniques described so far are based on direct processing of the remotely sensed imagery.An assumption of spatial dependence within and between pixels was used, to map the location within each pixel of the proportions output from a soft classification. The assumption proved to be valid for recreating the layout and areal coverage of the land cover. However, the algorithm attempted to cluster similar sub-pixels spatially by comparing sub-pixels to neighbouring pixels, thus mixing scales and producing linear artefacts in the output imagery.
The algorithm was applied to synthetic imagery and a SPOT HRV image of Sahelian wetlands. However, since the algorithm also compared sub-pixels to pixels, linear artefacts resulted in the super-resolution map.
This topic provides an overview of work done by the authors to develop a super-resolution land cover mapping approach that uses the output from a soft classification technique to constrain a Hopfield neural network formulated as an energy minimization tool. By actually mapping the location of land cover class components within each pixel, the technique manages to reduce the uncertainty of predictions produced through soft classification by converting them to single, hard super-resolution predictions. The majority of the remainder of this topic will focus on the basic mapping approach of the network, but an extension of the technique is also described.
Using the Hopfield Network for Land Cover Mapping at the Sub-pixel Scale
For the task of super-resolution land cover mapping, the basic design of the Hopfield neural network described in Tatem et al. (2001a) was extended to cope with multiple classes. The class proportion images output from soft classification are represented by h inter-connected layers in the network (where h is the number of land cover classes). Each neuron of largest output value within these layers corresponds to a pixel in the finer spatial resolution map produced after the network has converged. Therefore, neurons will be referred to by co-ordinate notation, for example, neuron (h,i,j) refers to a neuron in row i and column j of the network layer representing land cover class h, and has an input value of uhj and an output value of vhij. The zoom factor, z, determines the increase in spatial resolution from the original satellite sensor image to the new fine spatial resolution image. After convergence to a stable state, the output values, v, of all neurons are either 0 or 1, representing a binary classification of the land cover at the finer spatial resolution. The specific goals and constraints of the Hopfield neural network energy function determine the final distribution of neuron output values.
The input, u, to neuron with co-ordinates (h,i,j) is made up of a weighted sum of the outputs from every other neuron,
where N is the number of land cover classes,![]() represents the weight between neuron (h,i,j) and (a,b,c), and
represents the weight between neuron (h,i,j) and (a,b,c), and![]() is the output of neuron (a,b,c). The function describing the neural output at time t,
is the output of neuron (a,b,c). The function describing the neural output at time t,![]() , as a function of the input is,
, as a function of the input is,
where![]() is the gain, which determines the steepness of the function and
is the gain, which determines the steepness of the function and![]() lies in the range [0,1].
lies in the range [0,1].
The dynamics of the neurons are simulated numerically by the Euler method. After a user-defined time step, dt, the input to neuron![]() becomes,
becomes,
where![]() represents the energy change of neuron (h,i,j) at time t. The total energy change of the network is then,
represents the energy change of neuron (h,i,j) at time t. The total energy change of the network is then,
and when this reaches zero, or the change in energy from![]() is very small, the network has converged on a stable solution.
is very small, the network has converged on a stable solution.
The goal and constraints of the sub-pixel mapping task are defined such that the network energy function is,
For neuron![]() are the values of spatial clustering (goal) functions,
are the values of spatial clustering (goal) functions,
![]() is the value of a proportion constraint, and
is the value of a proportion constraint, and![]() is the value of a multi-class constraint. The constants
is the value of a multi-class constraint. The constants![]() are used to decide which constraint weightings to apply to solve the problem.
are used to decide which constraint weightings to apply to solve the problem.
The goal functions
The spatial clustering (goal) functions,![]() are based upon an assumption of spatial dependence. For neuron
are based upon an assumption of spatial dependence. For neuron![]() an average output of its neighbours for each land cover class
an average output of its neighbours for each land cover class![]() is calculated, which represents the target output for that neuron,
is calculated, which represents the target output for that neuron,
The first function aimed to increase the output for each layer, h, of the centre neuron, ![]() to 1, if the average output of the surrounding eight neurons,was greater than 0.5,
to 1, if the average output of the surrounding eight neurons,was greater than 0.5,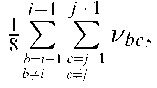
where![]() is a gain which controls the steepness of the tanh function. The tanh function controls the effect of the neighbouring neurons. If the averaged output of the neighbouring neurons is less than 0.5, then equation (7) evaluates to 0, and the function has no effect on the energy function (equation (5)). If the averaged output is greater than 0.5, equation (7) evaluates to 1, and the
is a gain which controls the steepness of the tanh function. The tanh function controls the effect of the neighbouring neurons. If the averaged output of the neighbouring neurons is less than 0.5, then equation (7) evaluates to 0, and the function has no effect on the energy function (equation (5)). If the averaged output is greater than 0.5, equation (7) evaluates to 1, and the![]() function controls the magnitude of the negative gradient output, with only
function controls the magnitude of the negative gradient output, with only![]() producing a zero gradient. A negative gradient is required to increase neuron output.
producing a zero gradient. A negative gradient is required to increase neuron output.
The second clustering function aimed to decrease the output for each layer, h, of the centre neuron,![]() to 0, given that the average output of the surrounding eight neurons,
to 0, given that the average output of the surrounding eight neurons,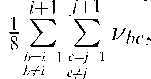 was less than 0.5,
was less than 0.5,
This time the tanh function evaluates to 0 if the averaged output of the neighbouring neurons is more than 0.5. If it is less than 0.5, the function evaluates to 1, and the centre neuron output,![]() controls the magnitude of the positive gradient output, with only
controls the magnitude of the positive gradient output, with only![]() producing a zero gradient. A positive gradient is required to
producing a zero gradient. A positive gradient is required to
decrease neuron output and only when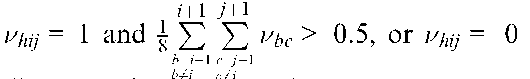
and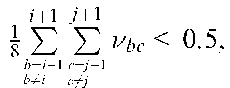 is the energy gradient equal to zero, and
is the energy gradient equal to zero, and![]()
This satisfies the objective of recreating spatial order, while also forcing neuron output to either 1 or 0 to produce a bipolar image.
The proportion constraint
The proportion constraint,![]() aims to retain the pixel class proportions output from the soft classification. This is achieved by adding in the constraint that for each land cover class layer, h, the total output from each pixel should be equal to the predicted class proportion for that pixel. An area proportion prediction,
aims to retain the pixel class proportions output from the soft classification. This is achieved by adding in the constraint that for each land cover class layer, h, the total output from each pixel should be equal to the predicted class proportion for that pixel. An area proportion prediction,![]() is calculated for all the neurons representing pixel (h,x,y),
is calculated for all the neurons representing pixel (h,x,y),
The tanh function ensures that if a neuron output is above 0.55, it is counted as having an output of 1 within the prediction of class area per pixel. Below an output of 0.55, the neuron is not counted within the prediction, which simplifies the area proportion prediction procedure, and ensures that neuron output must exceed the random initial assignment output of 0.55 to be counted within the calculations.
To ensure that the class proportions per pixel output from the soft classification were maintained, the proportion target per pixel, ahxy, was subtracted from the area proportion prediction (equation (9)),
If the area proportion prediction for pixel (h,x,y) is lower than the target area, a negative gradient is produced which corresponds to an increase in neuron output to counteract this problem. An over-prediction of class area results in a positive gradient, producing a decrease in neuron output. Only when the area proportion prediction is identical to the target area proportion for each pixel does a zero gradient occur, corresponding to![]() in the energy function (equation (5)).
in the energy function (equation (5)).
The multi-class constraint
The multi-class constraint,![]() aims to ensure that the outputs from each class layer fit together with no gaps or overlap between land cover classes in the final prediction map. This is achieved by ensuring that the sum of the outputs of each set of neurons with position (i,j) equals one.
aims to ensure that the outputs from each class layer fit together with no gaps or overlap between land cover classes in the final prediction map. This is achieved by ensuring that the sum of the outputs of each set of neurons with position (i,j) equals one.
If the sum of the outputs of each set of neurons representing pixel (i,j) in the final prediction image is less than one, a negative gradient is produced which corresponds to an increase in neuron output to counteract this problem. A sum greater than one produces a positive gradient, leading to a decrease in neuron output. Only when the output sum for the set of neurons in question equals one, does a zero gradient occur, corresponding to![]() in the energy function (equation (5)).
in the energy function (equation (5)).