Results Illustrating the Utility of the Conditional Distribution Representation
The previous section introduced a new way of representing information derived from remotely sensed data. Rather than explicitly extracting the quantity of interest – in this case, the proportion of a sub-pixel’s area covered by cereal crops – the new approach extracts a probability distribution that describes how consistent different values of the quantity of interest are with the reflectance that was observed. This new way of representing information extracted from remotely sensed data offers a wide range of benefits, which are discussed in this section, and fall under three headings, visualization, combination, and propagation.
Visualization
One of the most important benefits of representing estimated quantities as probability distributions is that the information about them that is contained in the remotely sensed data can be expressed fully. For example, the information in the distribution in Figure 4.15 would, in a more conventional representation, be approximated by the distribution’s mean, or at most, its mean and variance. Clearly, this results in almost all of the detailed information in the distribution, and hence in the remotely sensed data from which it was derived, being lost.
One problem with the representation is that although it provides detailed information about the different possibilities as to the sub-pixel composition of individual pixels, in itself, it is inappropriate for the representation of synoptic information for large numbers of pixels at once. This problem can be overcome, however, by summarizing the distributions associated with individual pixels by their means and variances, both of which can be efficiently calculated using the formulae provided in Bishop (1995), and can be used to form images, as shown in Figures 4.16 and 4.17.
The distribution means provide useful synoptic information because it is the estimate of the quantity of interest that minimizes mean squared error measured over the probability distribution and, in this sense, is the single value that summarizes it most accurately. The variance is useful because it provides information on how well the mean summarizes the distribution. A variance close to zero, for example, means that the entire probability distribution is centred close to a single point – its mean -which thus describes the distribution very well, as shown in Figure 4.18. A distribution with large variance, however, contains substantial probability mass away from its mean, indicating that the mean itself inadequately summarizes the range of values of the quantity being estimated, as shown in Figure 4.19.
Figure 4.16 The means of the distributions estimated by the MDN can be represented as images, and provide a convenient way of summarizing the information that they contain
Figure 4.17 The variances of the distributions estimated by the MDN can also be represented as images and provide a useful indication of how well the distributions are summarized by their means. Lighter pixels are associated with distributions that have large variances, and hence provide little information about sub-pixel composition. It is interesting to note that these occur mainly for mixed pixels along field boundaries where the PSF is expected to have a significant impact
Figure 4.18 In a distribution with small variance, nearly all the probability mass occurs close to the distribution’s mean. This indicates that, in most pixels, the class that the distribution was estimated for will occupy a proportion of the sub-pixel area very close to the distribution’s mean. In the above example, the distribution’s mean is represented by the solid vertical line, and its variance by the dashed lines
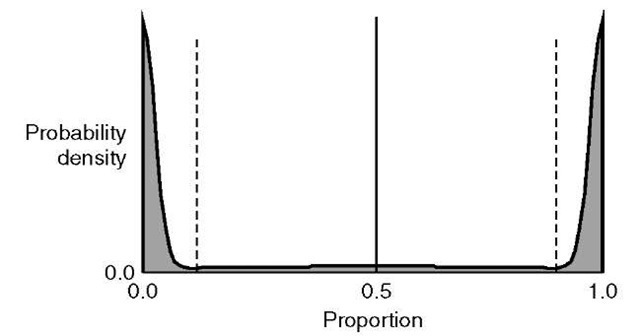
Figure 4.19 In a distribution with large variance, much of the probability mass occurs far from the distribution’s mean, making it a poor guide as to what proportions can occur. In the above example, the distribution’s mean is represented by the solid vertical line, and its variance by the dashed lines. It should be noted that, although the distribution’s mean is 0.5, proportions close to 0.5 are unlikely to occur, and those close to 0.0 and 1.0 can be expected to be far more common
When the probability distribution associated with a pixel has large variance, it is likely that a direct visualization of the entire distribution is likely to yield extra useful information. This concept is illustrated in Figure 4.20, where the distribution for a pixel with a large variance has been represented explicitly.
To reinforce the value of the synoptic information provided by images of the distribution means and variances.Not only are the distribution means very similar to the MLP’s proportion estimates, but the distribution variances are large in areas where each of these estimates corresponds poorly with the actual proportions.
Figure 4.20 If estimates of the proportions of the sub-pixel areas covered by different classes are represented as probability distributions, images of the distribution means (such as that shown to the left) provide a useful summary of the information in the distributions. For any pixel in the image, however, the full probability distribution can be extracted (as shown on the right) to reveal the full range of alternative possibilities
Figure 4.21 The magnitude of the squared differences between the distribution means and the sub-pixel proportions revealed by a ground survey. The similarity with Figure 4.17 suggests that the distribution variances provide a good indication of the likely accuracy of the distribution means as proportion estimates. Whiter pixels indicate greater difference
This suggests that the distribution variances provide a useful practical indication of the likely accuracy of the distribution means as estimates of the quantity of interest. As a final point, it is interesting to note that the distribution variances shown in Figure 4.17 tend to be large along field boundaries. These are the areas where pixels occur whose area is divided most evenly between classes, and where, from the earlier analyses, the sensor’s PSF would be expected to introduce most ambiguity.
Combination
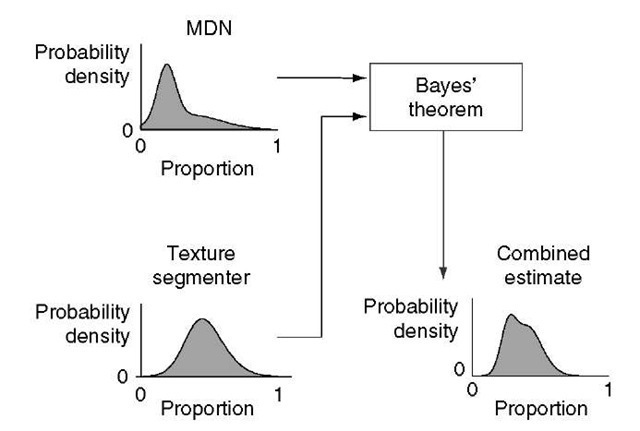
When trying to estimate a quantity of interest, such as the proportion of the area of a pixel that is covered by cereal crops, it is common that different estimates can be obtained from a variety of sources. For example, Figure 4.22 shows a system that contains two proportion estimators. The first of these, an MDN, uses pixel reflectances to estimate unique probability distributions over proportions for each one. The second segments the image according to the textures within it, and then, for each texture, estimates a unique probability distribution over proportions.
Figure 4.22 Representing information from different sources as probability distributions allows it to be combined optimally. This example shows how proportion information from a texture segmentation algorithm that has been modified to estimate the proportions of classes in a pixel based on the texture that surrounds it, can be combined with information extracted using an MDN. Bayes’ theorem provides a mathematical framework for combining sources of information without making assumptions or approximations. The result of a Bayesian combination is information that is always more specific than that contained in either of the original sources
Each pixel in the image thus has two estimates associated with it, one originating from the MDN and the other from the texture segmenter, both of which are represented by probability distributions. Fortunately, probability theory states that these information sources can be combined optimally using either Bayes’ theorem, or by marginalization (Bishop, 1995). If only the single ‘best’ proportion estimate was made available by either or both of the information sources, the estimates could not have been combined without making assumptions (typically, that the unknown distributions are Gaussian). Representing any estimated quantity by a probability distribution is thus extremely important as far as combining the estimate with information from other sources is concerned.
Propagation
Quantities that are extracted from remotely sensed data are frequently used as inputs to other systems and processes. For example, measurements of changes in the area of important cover types are often made by taking the difference between area estimates obtained from successive remotely sensed images. Since such estimates are ambiguous, however, it is reasonable to assume that the estimated change is also ambiguous. More generally, the output of any system or process that uses information from a remote sensor will be characterized by some ambiguity. Provided that all inputs to the system and process are represented by probability distributions, however, the ambiguity in the system’s or process’s output can be derived.
As an example, consider estimating the percentage change in the area of forest cover using successive remotely sensed images of the same region. To simplify the example, only a single pixel in each image is analysed and it is assumed that the two pixels sample exactly the same area of ground. If the same reflectance was associated with each pixel, state-of-the-art area estimation algorithms, such as neural networks, would estimate exactly the same area for the forest class in each case. This would inevitably lead to the conclusion that there had been no change in sub-pixel cover between the two observations.
Now consider analysing the pixels using an MDN. Like the neural network, the MDN makes the same estimate for the area of the forest class for each pixel, but represents its estimate as the probability distribution of Figure 4.23. This indicates that the sub-pixel area is likely to be exclusively forest, but could also contain no forest whatsoever. Using the techniques outlined in DeGroot (1989), it is possible to propagate the area estimate distributions produced by the MDN through the percentage change calculation so that the ambiguity in the percentage change estimate can also be represented as a distribution, as shown in Figure 4.24. As would be expected for an area that has not changed in reflectance, there is a large peak around 0% change, indicating that it is highly likely that no significant change in forest cover has occurred.
Figure 4.23 Estimates for the proportion of sub-pixel area covered by forest obtained on the first and second observation of the target area. Because the remote sensor measured the same reflectance on each occasion, the MDN made the same estimates
Figure 4.24 The distribution over the percentage change in the sub-pixel forest area that could have occurred between the observations. As expected, the large peak at 0% indicates that it is most likely that no change in sub-pixel cover took place. The smaller peak at -100% indicates that the pixel could have changed from being completely covered by forest to containing no forest at all, while the non-zero probability up to (and beyond) +300% shows that the proportion of the sub-pixel area covered by forest could have more than trebled
It is interesting to note, however, that there is also a peak around -100%, suggesting that the sub-pixel area could have changed from being covered completely by forest to containing no forest at all. In fact, all percentage changes from – 100% up have non-zero probabilities associated with them, and hence cannot be excluded on the basis of the remote observations.
It is important to emphasize that the uncertainty in the percentage change estimates in Figure 4.24 was also present in those obtained using the neural network based area estimates. In that case, however, since the neural network provided no representation of the ambiguity in its estimates, its effect could not be tracked through the percentage change calculation, and hence the ambiguity it induced in the percentage change estimate could not be represented. Provided that techniques that model explicitly the ambiguity in their estimates by probability distributions are used to extract information from remotely sensed data, the effect of the ambiguity implicit within such data can always be tracked and represented, regardless of where and how it is later applied.
Conclusions
This topic has presented new research into the effect of a remote sensor’s PSF on the information that it acquires. A sensor’s PSF describes the variation in sensitivity of the sensor to the reflectance of land cover within and around individual pixels. It was shown that this sensitivity variation is an important source of a particular type of uncertainty, known as ambiguity. Specifically, sensitivity variation can lead to the remote sensor observing the same reflectance for radically different mixtures of sub-pixel classes. Such differences cannot, therefore, be distinguished by a remote sensor, and hence a remote sensor can only provide highly ambiguous information about processes that occur at ground level. Although these arguments were presented in terms of estimating the areas of different cover types, they apply equally well to all information extracted from data acquired by remote sensors.
Section 4 described an advanced neural-statistical technique called a mixture density network, that offers important benefits when extracting information from remotely sensed data. Because the technique uses a probability distribution to represent the information it extracts, it can represent all the information contained in remotely sensed data. This richness of the representation is important for visualization, making all the information contained in remotely sensed data available to analysts. Perhaps more importantly, without the representation, systems that use estimates (either in combination with information from other sources, or in isolation) cannot, on average, behave optimally.
The research presented in this topic has implications for virtually all projects that use remotely sensed data. The techniques that have been presented provide a starting point for estimating the limits to the information that can be derived from remotely sensed data for any purpose (Wilkinson, 1996), and deriving such limits must form an important part of any research programme. For if it can be shown that the limit on the information that can be extracted from remotely sensed data has been reached, further research on more powerful analytical techniques cannot be justified.
At the same time, a wide range of new research opportunities emerge as a result of the possibility of propagating uncertainty, which, as was shown in section 5 can produce startling new results even in the simplest systems.