A Computational Analysis of the Ambiguity Induced by the PSF
This section describes an efficient computational technique for estimating bounds on the ambiguity induced by a sensor’s PSF. The technique can, in principle, estimate the bounds to arbitrary accuracy, and is limited in practice only by the computer power available to it. It works by alternately arranging one class in the area where the sensor is most responsive, moving it to the area where the sensor is least responsive, and measuring the increase or decrease in the area of the class that is required to leave the measured reflectance unchanged. As with the analytical technique discussed above, this assumes that the sub-pixel area is covered by only two classes, and that each exhibits no spectral variation. The validity and significance of these assumptions is discussed later.
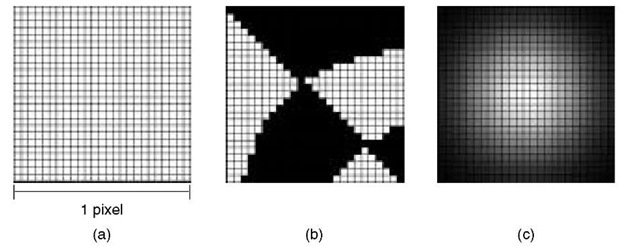
To simulate different sub-pixel arrangements of land cover, the sub-pixel area is represented as a fine grid, as shown in Figure 4.8(a), and each grid cell assigned to one of the two sub-pixel classes, as illustrated in the example in Figure 4.8(b). This allows any arrangement of two non-intergrading classes to be represented arbitrarily closely, provided that a sufficiently fine grid is used. The sensitivity profile of the sensor is represented on the same grid by calculating the value of the PSF at the centre of each cell, as shown in Figure 4.8(c). Again, this produces an arbitrarily close approximation to any smooth PSF, provided that a sufficiently fine grid is used.
Figure 4.8 Components of the technique. (a) The sub-pixel area is shown divided into a regular grid of 25 x 25 cells. (b) Different arrangements of sub-pixel cover are approximated by assigning each cell to one of the sub-pixel classes. The arrangement shown could correspond to several fields divided between two crop types, for example. (c) The PSF of the sensor can also be approximated on the grid by assigning each cell a value equal to the PSF at the cell’s centre. These values are represented as shades of grey in the figure, with white representing greatest sensitivity.
Using the grid-based representation of the sub-pixel area, the lower bound on the PSF-induced ambiguity can be determined in the following way, assuming that the black class covers a proportion ^ of the sub-pixel area:
1. Distribute the black class in the area where the PSF is least sensitive by assigning grid cells within the pixel to the black class, starting with the cells for which the PSF is least sensitive, and finishing once the class covers a proportion ^ of the sub-pixel area.
2. Compute the apparent reflectance of the pixel by finding the sum of the PSF values for all cells that are covered by the black class.
3. Set all grid cells back to white.
4. Distribute the black class in the area where the PSF is most sensitive by assigning cells to it, starting with those for which the PSF is most sensitive, and finishing when the apparent reflectance of the pixel – computed in the same way as in step 2 – is the same as that computed in step 2.
5. The lower bound on the PSF-induced ambiguity for a pixel where a class covers a proportion ^ of the sub-pixel area is given by the proportion of the pixel’s area covered by the black class after step 4.
The upper bound may be computed by the reverse of the above procedure by, in step 1, distributing the black class where the PSF is most sensitive and moving it to where the PSF is least sensitive in step 4.
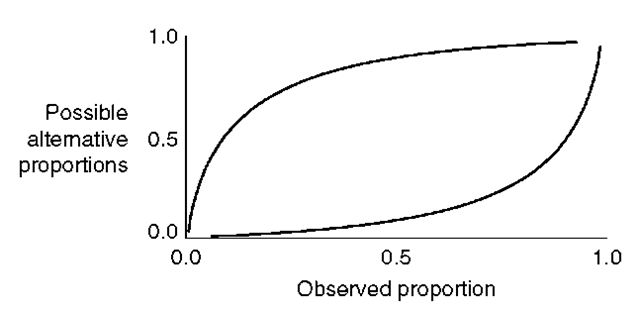
By repeating steps 1 to 5 for a range of values of ^ between zero and one, the bounds can be plotted in the same way as the analytically derived ones were in the previous section. Figure 4.9 shows the bounds derived for the Gaussian PSF model using a grid size of 50 by 50 cells. The similarity of these bounds to those derived using the analytical method of Manslow and Nixon (2000) indicates that the grid-based representation of the arrangement of sub-pixel cover has minimal impact on the accuracy of the estimated bounds, at the selected spatial resolution, for the Gaussian PSF.
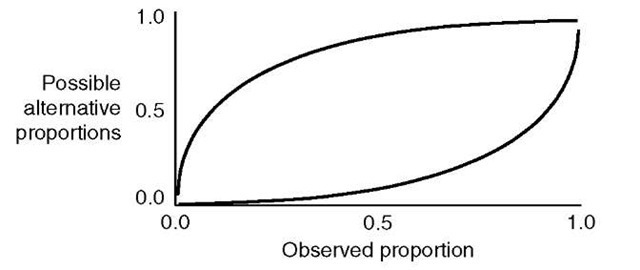
Figure 4.10 shows the bounds derived for a cosine PSF model, which is shown in Figure 4.11. Despite the differences between the Gaussian and cosine models, the shape of the bounds on the ambiguity they induce are almost identical. This is because the main difference between the models occurs close to the pixel perimeter, where the sensitivity of the cosine model drops to zero. This causes the ambiguity induced by the cosine PSF to be larger for almost pure pixels – those that are covered almost completely by a single class – than for the Gaussian PSF.
Figure 4.9 Bounds on the ambiguity induced by the Gaussian PSF with parameter a = 2 calculated by the computational technique
Figure 4.10 Bounds on the ambiguity induced by the cosine PSF predicted by the computational technique. It is interesting to note the close resemblance to those predicted for the Gaussian PSF
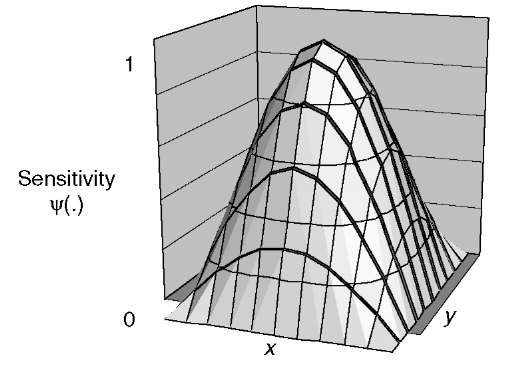
Figure 4.11 A cosine model of a PSF
The interpretation of PSF ambiguity bounds must be carried out with reference to the distribution of the proportion parameter ^ that is likely to be observed in a particular application. As an example, consider estimating the area of two cereal crops from SPOT HRV data. In this case, because individual fields are much larger than the ground area covered by a pixel, most pixels will consist of a single crop type, and only the small number of pixels that straddle field boundaries will contain a mixture of classes (see Kitamoto and Takagi, 1999, for a discussion of the relationship between the distribution of ^ and the spatial characteristics of different cover types). This means that ^ will be close to zero or one for most pixels, which is where the bounds are closest together, indicating that the PSF will have minimal effect.
When a pixel contains an almost equal mixture of two classes, however, the proportion ^ of each is close to 0.5, and hence the pixel lies towards the centre of the bound diagram where the upper and lower bounds are furthest apart, the PSF induces most ambiguity. In this case, the exact form of the ambiguity is a complex function of the spatial and spectral characteristics of the particular sub-pixel classes, which is difficult to derive analytically, and, in any case, is specific to each particular application. Rather than pursue this analysis in detail, a technique for modelling the ambiguity in information extracted from remotely sensed data, which can be applied in any application, is described in the next section.
The algorithm for estimating bounds on PSF-induced ambiguity that has been described in this section has made a number of assumptions and approximations. These have been necessary to reduce the problem to the point where analysis is actually possible, and to make the results of the analysis comprehensible. One source of ambiguity that has been ignored throughout this analysis is the overlap between the PSFs of neighbouring pixels, that was briefly described in an earlier section. Townshend et al. (2000) consider this issue in detail, and describe a technique that can be used, in part, to compensate for it.
In the analyses discussed above, it has been assumed that sub-pixel classes exhibit no spectral variation. In practice, however, real land cover classes do show substantial variation in reflectance, and this considerably complicates the analysis of a PSF’s effect. In addition, the differences in reflectance variation between and within classes make it difficult to maintain the generality once these are included in the analysis, because the results that would be derived would be specific to particular combinations of classes. Spectral variation was ignored in the analyses presented in this topic to maintain this generality, and to provide a clearer insight into the basic effect of the PSF.
Additional information on sources of ambiguity in remotely sensed data can be found in Manslow et al. (2000), which lists the conditions that must be satisfied for it to be possible, in principle, to extract error-free area information from remotely sensed data. The conditions must apply even in the case of the ideal PSFs, which were described in an earlier section, and require classes to exhibit no spectral variation, and for there to be at least as many spectral bands as classes in the area being sensed. Clearly, such conditions cannot be met in practice, indicating that additional sources of uncertainty cause the total ambiguity in area information derived from remote sensors to be greater than that originating within the PSF alone.
Extracting Conditional Probability Distributions from Remotely Sensed Data using the Mixture Density Network
The previous sections of this topic have focused on developing analytical tools that can provide very precise descriptions of the effect of a sensor’s PSF on the information the sensor acquires. Although it has been possible to gain new insights into the limitations imposed by the PSF, the PSF itself is only one of many sources of ambiguity, and indeed, one that is still not fully understood. The remote sensing process as a whole is so complex, that there will probably never be a general theoretical framework that allows the ambiguity in remotely sensed data to be quantified. This topic, therefore, describes an empirical-statistical technique that is able to estimate the ambiguity directly.
To clearly illustrate the techniques discussed in this section, they were used to extract estimates of the proportions of the sub-pixel areas of pixels in a remotely sensed image that were covered by a class of cereal crops. The area that was used for this study was an agricultural region situated to the west of Leicester in the UK.
A remotely sensed image of this area was acquired by the Landsat TM, and the area was subject to a ground survey by a team from the University of Leicester as part of the European Union funded FLIERS (Fuzzy Land Information in Environmental Remote Sensing) project to determine the actual distribution of land cover classes on the ground.
From the ground survey, it was possible to provide an accurate indication of the true sub-pixel composition of every pixel in the remotely sensed image. Figure 4.12(a) shows band 4 of the image, and Figure 4.12(b) shows the proportions of each pixel that were found to be covered by cereal crops during the ground survey. In all, the data consisted of roughly 22 000 pixels, the compositions of which were known.This would be done by using the pixels of known composition to teach the neural network the relationship between a pixel’s reflectance and its sub-pixel composition. Once the neural network has learned this relationship, it can be applied to pixels of unknown composition – the network is given the pixels’ reflectances, and responds with estimates of their composition.Although there is a fairly reasonable correspondence between the actual proportions (shown in Figure 4.14) and the estimates, there are important differences.
The differences between the actual and estimated class proportions have many causes, not least of which is the ambiguity introduced by the sensor’s PSF. One of the weaknesses of the neural network approach to estimating sub-pixel composition is that it can only associate a single proportion estimate with every pixel – even though remotely sensed data contains too little information to state unambiguously what proportion of a pixel’s area is covered by any class. This limitation is not just a failure to express the ambiguity in the estimate, but also to express all the information contained in the remotely sensed data. For example, the neural network may state that 63% of the sub-pixel area is covered by cereal crops, but does not indicate that, in reality, cereal crops may cover anywhere between 12 and 84% of the area.
Figure 4.12 The area from which data were collected for the experiments described in this topic. (a) shows the remotely sensed area in band 4. The regions within the white squares are magnified to provide greater detail in later figures. (b) The proportions of sub-pixel area covered by cereal crops represented on a grey scale. White indicates that a pixel was purely cereal, and black indicates that no cereal was present
Figure 4.13 The proportions of sub-pixel areas that were predicted to be covered by cereal crops using a neural network for the four regions highlighted in Figure 4.12. White corresponds to a pixel consisting purely of cereal, whereas black corresponds to a pixel containing no cereal at all. Here, and in later figures, the checkered areas were outside the study area and were not used
Figure 4.14 The real proportions of sub-pixel area that were covered by cereal crops, as determined by a ground survey
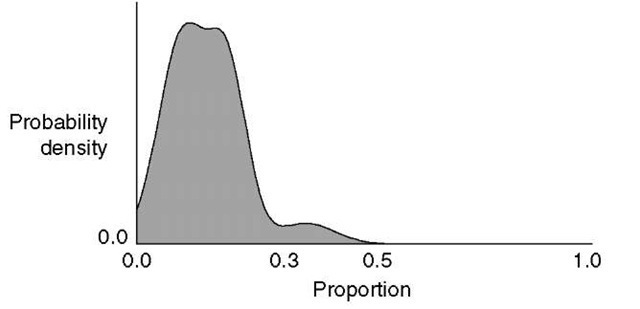
The above suggests that a more flexible representation is needed that is able to express fully not only the ambiguity, but also all the information in the remotely sensed data. Figure 4.15 shows a representation that can do this – the probability distribution over the sub-pixel proportion estimate. The principle behind this representation is that it not only represents the range of proportions that are consistent with the reflectance of the pixel, but also how consistent particular values are. For example, the distribution in Figure 4.15 indicates that, although the sub-pixel area could be covered by anything between about 0 and 50% by cereal crops, it is most likely to be around 0 to 30%. This type of representation is information rich, and can summarize all the ambiguity in the remote sensing process, regardless of its source.
In order to extract proportion distributions, a technique will be used that was first introduced by Bishop (1994) and is further described in Bishop (1995). The mixture density network (MDN) is similar to a neural network both in structure and in operation, and can use exactly the same data without the need for any special preparation. Like the neural network, the MDN must be taught the relationship between pixel reflectances and their sub-pixel composition by being shown a large number of pixels of known composition. Details of how this is done can be found in Bishop (1994) and Manslow (2001). Once the MDN has learned the relationship between pixels’ reflectances and the proportions with which sub-pixel classes are present, it can be used to extract a proportion distribution for a pixel of unknown composition.
Figure 4.15 An example of how a probability distribution can be used to represent information extracted from remotely sensed data. In this example, the proportion of the sub-pixel area covered by cereal crops is estimated. The distribution explicitly represents the ambiguity in the estimate – the actual proportion is most likely to lie between about 0.00 and 0.30, but could be anywhere between 0.00 and 0.50
To do this, the pixel’s reflectance is applied to the MDN’s spectral inputs, and a range of proportions (such as 0.00, 0.01, …, 0.99 and 1.00) applied to its proportion input. For each value of the proportion input, the MDN responds with the posterior probability (density) that a pixel with the specified reflectance contains the specified proportion of the class of interest – in this case, cereal crops. Plotting these probabilities, as shown in Figure 4.15, provides a convenient way of representing the distribution. The following section presents some results that were obtained by using a MDN that was taught using a data set acquired for the FLIERS project, to estimate the distribution of the proportion of sub-pixel area that was covered by cereal crops.