Introduction
To introduce the problem addressed in this topic, let us look at the following example. Figure 10.1a shows a Digital Elevation Model (DEM) of a 2 x 2.5km area in the Vorarlberg region in the Austrian Alps. Figure 10.1b shows the corresponding slope map, computed with a second-order finite difference method (Skidmore, 1989).
As we are well aware, the DEM is only an approximation of the real elevation in the area. It contains errors. Our interest now is in how these errors propagate to the slope map. Let us assume that the DEM error at each location is ± 10m. We now use the Monte Carlo method to analyse how the error propagates.
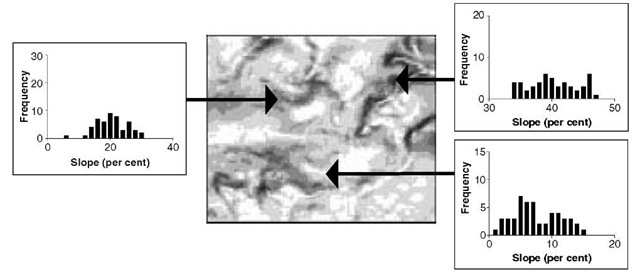
For those readers who are not familiar with the Monte Carlo method, let us briefly describe how it works. First, we generate a realization of the uncertain DEM, by adding, at each location, a random number drawn from the error probability distribution to the DEM elevation. Once this is done for all locations (i.e. all grid cells), we compute the slope map for this realization, and we store it. This procedure we repeat many times (typically between 50 and 200 times). From the collection of slope maps we can then determine how the uncertainty in the DEM has propagated to the slope, for instance by looking at the width of the histogram of the slope values at locations. This is illustrated in Figures 10.2 and 10.3.
The above simple example illustrates the ease with which an error propagation analysis may be carried out. The example is simple, but in fact the Monte Carlo method can as easily and as straightforwardly be applied to more complicated GIS operations or spatial models (see Nackaerts et al., 1999; De Genst et al., 2001; Endreny and Wood, 2001; Canters et al., 2002, for some recent examples). The only disadvantage is that it is computationally demanding, but nowadays this can hardly be considered a real problem, particularly as the method lends itself perfectly to a parallel computing approach.
Figure 10.1 Example data sets. (a) Digital Elevation Model (metres) of a 2 x 2.5 km area in the Vorarlberg region in the Austrian Alps; (b) slope map (per cent) of the same area
Figure 10.2 Top: four simulated DEMs constructed by adding a simulated error map to the DEM of Figure 10.1. Bottom: associated slope maps
Figure 10.3 Histograms of simulated slope values (for three arbitrary locations and computed from 50 Monte Carlo runs) characterize how uncertainty in the DEM propagates to slope
From the above, some may be tempted to conclude that the problem of error propagation in GIS is solved: ‘Monte Carlo simulation solves all our problems’. Is this really true? Unfortunately, it is not. There are still a large number of important problems to be resolved. Some of them fairly easy, many of them very difficult. In this topic we will review several of them. We will explain what these problems are, and try to indicate how they may be tackled. Although the aim is to address a variety of problems, no attempt is made to be complete. Also, the discussion is biased towards problems that have a geostatistical angle to them.
Spatial Error Cannot be Reduced to a Single Number
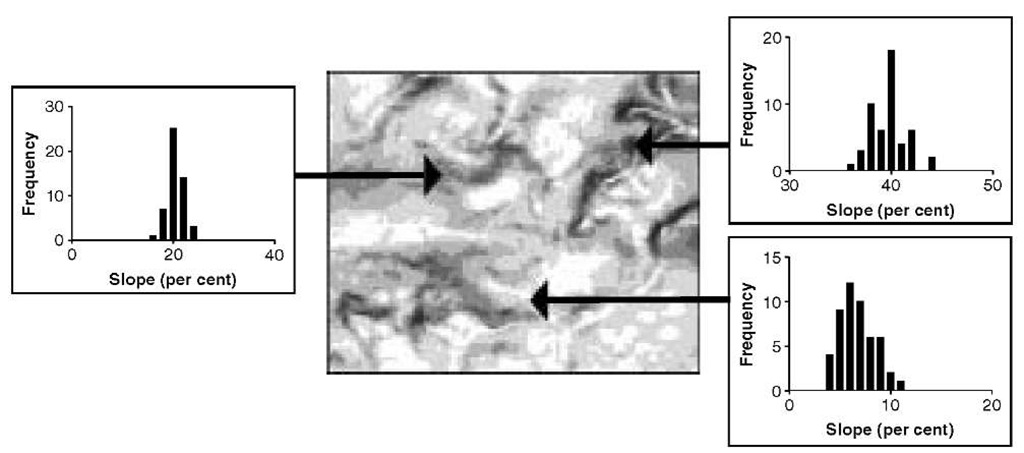
In the Vorarlberg example we stated that the error in the DEM was ± 10 m. We did not discuss how we came to this number, and neither did we discuss whether we had completely characterized the DEM error by just one number. To answer this last question, we definitely had not. To completely specify the DEM error at some location we need its full probability distribution (i.e. its shape and its parameters), otherwise we could not conduct the Monte Carlo analysis. To simulate the DEM error it was assumed that the error was normally distributed with zero mean and a standard deviation equal to 10 m. It was also assumed that this was the case for all locations, regardless whether it concerned a relatively flat or steep part of the area, or whether there were control points nearby or not. By sampling at each grid cell independently, it was also assumed implicitly that the error was spatially uncorrelated. This is a critical assumption. If we had assumed that there was spatial autocorrelation in the DEM error, say such that it was characterized by a semi variogram with zero nugget variance and a correlation length (i.e. ‘range’) of 1 km, then the results of the uncertainty analysis would have been entirely different (see Figure 10.4). This is because slope calculations are extremely sensitive to the degree of spatial autocorrelation in the DEM errors (Heuvelink, 1998, section 5.2). Clearly, if the results of the uncertainty analysis are to have any value, it is crucially important to assess realistically the degree of spatial autocorrelation in the DEM error.
Figure 10.4 Histograms of slope values (for the three example locations and computed from 50 Monte Carlo runs) characterize how the uncertainty in DEM propagates to slope predictions. In this case the DEM error is spatially autocorrelated with zero nugget variance and a spatial correlation length of 1km. Comparison with Figure 10.3 shows that taking positive spatial autocorrelation in DEM error into account reduces the uncertainty in slope predictions.
By failing to specify completely the DEM error, we in fact used ‘default’ values for the unspecified parameters. However, assuming by default that the error standard deviation is the same throughout the area and assuming by default that spatial autocorrelation is absent may not be very sensible. Instead, we should use realistic parameter values. How can we do this? How can we estimate these parameters? The most appropriate way to go about this is to rely on geostatistics. Geostatistics is a well-developed discipline that is dedicated to the statistical analysis of spatially varying properties (Kitanidis, 1997). Geostatistics provides the theory to define properly spatial errors, and it provides the instruments to estimate the parameters of the error model from point observations or other information sources. It even aids in carrying out Monte Carlo uncertainty analyses, by offering tools that can generate realizations of spatially correlated errors (Goovaerts, 2002). The body of theory and methods encompassed by geostatistics is large and continues to grow. It allows the handling of anisotropy, non-stationarity, non-normality and much more (Goovaerts, 1997).
A problem is that to use geostatistics responsibly requires a fair amount of background in statistics. Also, users must invest time and show a willingness to learn geostatistics. Can we reasonably expect this of the ‘ordinary’ GIS user who just wants to do an uncertainty propagation analysis? Often, this will be too much to ask of the ordinary user. The solution is to make sure that the error specification of the inputs to the uncertainty analysis are derived by experts and then stored in the GIS database for later use. Indeed, the GIS research community has been working already for quite some time on establishing a so-called ‘error-aware’ GIS, that also stores quality information about the data stored in the GIS database (Duckham, 2000; Qiu and Hunter, 2002). However, ‘In spite of a growing demand from the user community for more appropriate documentation on spatial data quality, and the existence of established standards for doing so, in most cases meta-information on the accuracy of spatial data is lacking or is limited to simple, overall measures that do not describe spatial variation in error’ (Canters et al., 2002). We will return to this issue in the concluding section of this topic.
The Case of Multiple Uncertain Inputs
Again, for illustrative purposes, let us now turn to another, more complicated error propagation example.
The soil acidification model SMART2 (Kros et al., 1999) is a fairly simple, strictly vertical, one layer dynamic model that predicts the long-term response of aluminium (and nitrate) concentration below the root zone to changes in atmospheric deposition. The model was developed to analyse how atmospheric deposition causes soil acidification and how this, in turn, affects the groundwater quality.
At the European scale, the inputs to SMART2 have to be derived from general-purpose soil and vegetation type maps. These maps are not very accurate. In addition, the mapping procedure involves the use of transfer functions to transform map information to specific soil and vegetation-related parameters required by SMART2, and this further deteriorates the quality of the model input. In order to judge whether the application of SMART2 at the European scale yields results that are sufficiently accurate, a study was carried out to analyse how the uncertainty in the source maps and the transfer functions propagate to the model output. This was done using a Monte Carlo approach.
The uncertainty analysis that was carried out treated 11 soil-related variables and eight vegetation-related inputs as uncertain. To run the analysis, for all 19 inputs error probability distributions and spatial correlation functions had to be specified. This was not an easy job, because little ‘hard’ information (i.e. field observations) was available to estimate the accuracy of the input data and transfer functions. For many parameters of the error distribution, one simply had to rely on expert judgements. This is acceptable when there is nothing else to rely on, but it is far from ideal. Expert judgements are no substitute for objective measurements.
One important class of parameters that needed to be specified as well were the correlations between the uncertainties in the input variables. With 19 inputs, there are 1/2 x 19 x (19 – 1) = 171 correlations to be assigned. Or even worse, there are 171 cross-correlation functions to be specified, because the uncertainty analysis requires the correlation between the error in input variable v,- at location xk and the error in input vj at location xl. Again, geostatistics provides the means to assess these cross-correlations, but only when there are sufficient observations of all attributes involved at a fairly large number of locations. And even then, identifying all these semivariograms and cross-semivariograms is a laborious and tedious job, which cannot easily be automated.
In the SMART2 case, a large number of cross-correlation functions were either known to be or assumed to be zero. This is not strange, because when two spatial attributes, such as the nitrification and denitrification factors, are correlated, the errors associated with these attributes may well be uncorrelated. Nonetheless,increasing the number of uncertain inputs causes a much greater increase in the number of estimated parameters. Also, storing such information in a spatial database is tricky, because whenever an uncertain variable is added to the database, the spatial cross-correlation with all other uncertain variables already stored in the database must also be assessed. Moreover, to avoid ending up with negative error variances for combinations of inputs, the so-called non-negative definiteness condition must always be satisfied. For instance, when the correlation between variables X and Y equals 0.9 and that between X and Z equals 0.9 as well, then the correlation between Y and Z cannot be smaller than 0.62 or negative-definite correlation matrices may result. Fast checking for non-negative definiteness is not easy when the number of uncertain variables is large and when, in addition, correlation varies with distance. Should we expect the non-statistician to be able to deal with these complex issues? No, we should not.
Incorporating Uncertainty in Categorical Inputs
In the SMART2 case study there were also two uncertain categorical inputs. These were soil and vegetation type. Including uncertain categorical inputs into the uncertainty analysis increases dramatically the complexity of the analysis, as we shall now see.
The soil map had only seven classes, the vegetation map only four. But soil and vegetation are not independent and, therefore, it was necessary to consider the 28 combined soil-vegetation classes. The soil-vegetation map is uncertain, and this means that when the map states that at some location the soil-vegetation is in class svj, in reality the soil-vegetation at that location may be in class svi (i f j). To quantify the uncertainty, we must provide the conditional probabilities py = ^(reality = svi |map = svj). In the case of 28 classes, there are 282 = 784 conditional probabilities to be predicted. The seconditional probabilities can be stored in the so-called error or confusion matrix, as it is often termed in the remote sensing literature.How can these probabilities be obtained? One possibility is to derive them from a comparison of the map with ground-based observations. However, this requires quite a large number of observations. Another possibility is to use a much more accurate map as a surrogate for the ‘truth’ (Finke et al., 1999). Yet another possibility is to embed the computation of the probabilities in the mapping procedure. For instance, discriminant analysis gives the probabilities as a byproduct in a supervised classification procedure. The latter also allows the error matrix to vary with location.
Even though there are methods to assess the many parameters that quantify the conditional probability distributions, it is important to recognize that when input variables are dependent (as is often the case) one quickly ends up with very large numbers of parameters. In the SMART2 case, we purposely reduced the number of soil classes to m = 7 and the number of vegetation classes to n = 4, yielding a manageable number of m • n = 28 combined classes, but what if m and n had been much greater than the numbers used? Or what if a third categorical variable had been added to the uncertainty analysis? The number of parameters to be estimated quickly explodes, rendering their reliable estimation unfeasible, and so we must find ways to get around this problem.
An obvious solution is to make additional assumptions that reduce greatly the number of parameters to be estimated. To illustrate some approaches, let us continue the example where we seek the conditional probability that soil type at some location equals![]() and that vegetation equals
and that vegetation equals![]() given that the soil map states that the soil type at that location equals
given that the soil map states that the soil type at that location equals![]() and that vegetation type equals
and that vegetation type equals
![]() There are
There are![]() parameters to be estimated. One
parameters to be estimated. One
way to reduce the number of parameters is to assume that:
where S stands for soil, V for vegetation, SM for soil map and VM for vegetation map. With equation (1), the number of parameters is reduced greatly from![]() to
to ![]() but only at the expense of the very strong assumption of statistical independence, which does not seem very realistic for the example of soil type and vegetation type.
but only at the expense of the very strong assumption of statistical independence, which does not seem very realistic for the example of soil type and vegetation type.
An alternative approach is to assume that:
This reduces the number of parameters to be estimated to![]() while not denying the dependence between soil type and vegetation. Instead, it assumes that the dependence between the two is not affected by the conditioning. Whether this is a more realistic assumption remains to be seen. As far as I know this has not yet been investigated.
while not denying the dependence between soil type and vegetation. Instead, it assumes that the dependence between the two is not affected by the conditioning. Whether this is a more realistic assumption remains to be seen. As far as I know this has not yet been investigated.
Although many map users would be very happy if an error matrix were available to summarize the accuracy of the categorical map, it is important to realize that in fact the error matrix does not provide all the information required to carry out an error propagation analysis. What is lacking is information about spatial dependence in the errors. After all, it is more than likely that the errors are spatially dependent, because similar errors are made at nearby locations. Recently, geostatistical procedures have been proposed to handle the spatial dependencies in errors in categorical maps (Finke et al., 1999; Kyriakidis and Dungan, 2001). These procedures, that are largely based on indicator geostatistics, are promising but they suffer from the same problem mentioned in the previous sections: to use them requires a solid background in (geo)statistics. Again, can we expect this from the ordinary GIS user who just wants to carry out an uncertainty analysis?
Scale Problems
Let us continue the SMART2 example. Although SMART2 is intended to be used at the regional scale (De Vries et al., 1998), it is still a model operating at the point support. This is because the model is based on differential equations that may be discretized but not to too large time and space steps and because the model parameters were calibrated on measurements taken on a point support (i.e. measurements the size of about 1 dm3). In order to assess groundwater quality at the European scale (5 km x 5 km and larger blocks), the model was therefore applied to many point locations within each block (Heuvelink and Pebesma, 1999). After the model was run at these point locations, the model outputs were aggregated to yield a single block value. For a single block, a single Monte Carlo run gives the output at all points in the block. These can be represented in a single graph by a cumulative distribution function. However, due to input uncertainty there will be a population of graphs, since each Monte Carlo run produces a different graph. In Figure 10.5, the population of graphs is represented by the sides of a 90% prediction interval. From it, we can construct 90% prediction intervals for quantiles, such as the median (Figure 10.5a) or for the block areal fraction exceeding a fixed concentration (Figure 10.5b).
It now turns out that the results of the uncertainty analysis depend greatly on the support of the data used in the analysis (Heuvelink, 1999). The larger the block, the smaller the uncertainty. This is because more and more variability averages out when the block size is increased. Readers that are familiar with kriging will see here the similarity with block kriging: block kriging variances are smaller than point kriging variances and become smaller and smaller as the block size increases. In other words, the results of an uncertainty analysis are only meaningful when the support of the output is stated, and when it matches the support required by the user.
In practice, it may occur frequently that the support of the obtained output does not match the desired output support. This calls for a ‘change of support’, which is more often in the form of an aggregation than a disaggregation. Existing techniques can be used to perform the aggregation or disaggregation, but it is not always very easy (Bierkens et al., 2000).
It is crucially important to recognize that the inputs and their associated errors must also be provided on the correct support. For instance, let precipitation and infiltration capacity be two uncertain inputs to a hydrological model.
Figure 10.5 Prediction intervals: (a) the 90% prediction interval for the median concentration in the block is [0.23, 2.15], (b) the 90% prediction interval for the areal fraction where point concentration values do not exceed 1 mol m-3 is [0.155, 0.930]
Let infiltration capacity be measured on a support of 1 m2, and let precipitation be measured using rain gauges with a surface area of 0.01 m2. Both attributes are interpolated to create spatially exhaustive inputs to the hydrological model. Interpolation error is quantified and its propagation through the model is analysed. It should now be clear that either infiltration capacity and its associated uncertainty must first be disaggregated or precipitation and its associated uncertainty must first be aggregated before the uncertainty propagation analysis can commence. Otherwise the results of the uncertainty analysis are effectively meaningless.
The effect of using wrong (combinations of) supports on the validity of the results of uncertainty analyses can hardly be underestimated. Here we have only stipulated it, but it deserves much attention. It can create tremendous problems, even in seemingly very simple applications. A good example of this for lead pollution is given in Heuvelink (1999).
Conclusions
We started this topic with the observation that to carry out an uncertainty analysis seemingly is not that difficult, because ‘Monte Carlo simulation solves all our problems’. However, by looking a bit further and by addressing several aspects of spatial uncertainty analysis, we then saw that there are still a large number of serious problems to be resolved. In particular, we discussed difficulties in the assessment of input error, both for continuous and categorical spatial attributes, and problems concerning the scale or support of model entities. We did not pretend to have a complete list of problems. For instance, we did not mention that in many cases the results of a GIS analysis are used as input to an ensuing operation. If we want to be able to keep track of how uncertainties propagate in chains of operations, then we must store the uncertainty of the output of each and every operation. This means storage of the output error probability distribution, its support, its spatial autocorrelation and, most importantly, its cross-correlation with all other uncertain attributes already stored in the database. Do we have procedures and databases that can accomplish this?
A returning theme of all problems discussed is that we require a lot of the user who wants to carry out an uncertainty analysis. Too much perhaps. We more or less expect the user to be an expert in (geo)statistics, or at least to have an expert in his or her immediate surrounding. We also expect him or her to accept that the uncertainty analysis requires lots more time (both computing time and user time) than the operation itself. The calculations take much longer, there are so many more parameters to be determined and stored and there are so many more output parameters to be stored and analysed. Can we reasonably expect the ‘ordinary’ GIS user to spend so much extra time? And all this just to get to know how accurate the result of an analysis is?
It is now time to become realistic and admit that the majority of GIS users are not prepared or even allowed to go to so much trouble. Many of them need to account for every hour spent and are expected to run projects on a cost-effective basis. In many cases, running a complicated uncertainty analysis simply does not pay off. This seems to be the main reason why the large-scale application of error propagation tools in GIS is as yet unrealized, in spite of the high hopes expressed now more than a decade ago (Goodchild and Gopal, 1989; Openshaw et al., 1991; Burrough, 1992).
What can be done about it? One solution that we may look into in the coming years is to seek ways that dramatically simplify the uncertainty propagation analysis, without seriously damaging the validity of the results of the analysis. Finding such ways is a true challenge. There is no guarantee for success. If successful, the result is not likely a set of simple rules such as ‘ignore spatial cross-correlation’, or ‘pretend that there are no scale problems’. It will undoubtedly be more refined, with different rules in different situations.
The degree of simplification may also be user-dependent. We could imagine this as follows. At the start of a session, the system would ask the user to qualify himself as an error propagation expert, a GIS professional or an amateur. Depending on this, the system would decide whether to ask the user to specify a parameter or to use a default value instead (of course, the difficulty is finding the right default values). After all, there is no sense in asking an amateur ‘warning: linear model of coregion-alization not satisfied. Do you wish to continue with the current settings?’. Amateurs want to be asked as little as possible, the uncertainty analysis has to run almost by itself. Only then can we truly speak about having extended GIS with a general purpose ‘error button’. In spite of the negative sides to a dramatic simplification of the error propagation analysis, this may still be preferred over a complete ignorance of how errors propagate in GIS analyses.


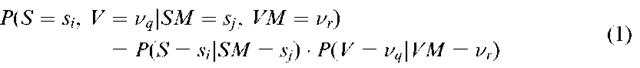
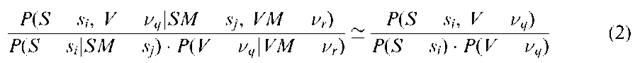
![Prediction intervals: (a) the 90% prediction interval for the median concentration in the block is [0.23, 2.15], (b) the 90% prediction interval for the areal fraction where point concentration values do not exceed 1 mol m-3 is [0.155, 0.930] Prediction intervals: (a) the 90% prediction interval for the median concentration in the block is [0.23, 2.15], (b) the 90% prediction interval for the areal fraction where point concentration values do not exceed 1 mol m-3 is [0.155, 0.930]](http://what-when-how.com/wp-content/uploads/2012/02/tmp255362_thumb.png)
