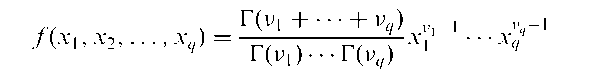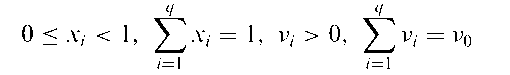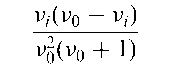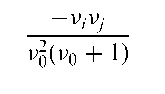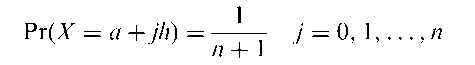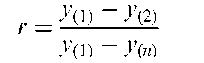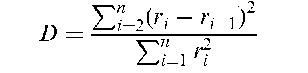Digraph:
Synonym for directed graph.
DIP test:
A test for multimodality in a sample, based on the maximum difference, over all sample points, between the empirical distribution function and the unimodal distribution function that minimizes that maximum difference.
Directed acyclic graph:
Synonym for conditional independence graph.
Directed deviance:
Synonymous with signed root transformation.
Directional neighbourhoods approach (DNA):
A method for classifying pixels and reconstructing images from remotely sensed noisy data. The approach is partly Bayesian and partly data analytic and uses observational data to select an optimal, generally asymmetric, but relatively homogeneous neighbourhood for classifying pixels. The procedure involves two stages: a zero-neighbourhood pre-classification stage, followed by selection of the most homogeneous neighbourhood and then a final classification.
Direct matrix product:
Synonym for Kronecker product.
Direct standardization:
The process of adjusting a crude mortality or morbidity rate estimate for one or more variables, by using a known reference population. It might, for example, be required to compare cancer mortality rates of single and married women with adjustment being made for the age distribution of the two groups, which is very likely to differ with the married women being older. Age-specific mortality rates derived from each of the two groups would be applied to the population age distribution to yield mortality rates that could be directly compared.
Fig. 54 Digit preference among different groups of observers. For zero, even, odd and five numerals.
Dirichlet distribution:
The multivariate version of the beta distribution. Given by
where
The expected value of xt is v/v0 and its variance is
The covariance of xt and Xj is
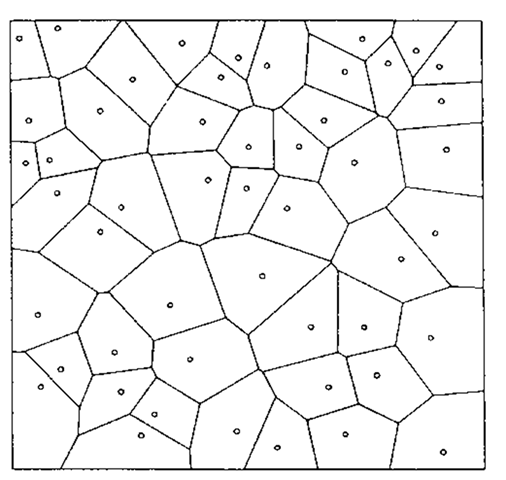
Dirichlet tessellation:
A construction for events that occur in some planar region A, consisting of a series of ‘territories’ each of which consists of that part of A closer to a particular event xt than to any other event Xj. An example is shown in Fig. 55.
Discrete rectangular distribution:
A probability distribution for which any one of a finite set of equally spaced values is equally likely. The distribution is given by
so that the random variable X can take any one of the equally spaced values a, a + h,…, a + nh. As n ! 1 and h ! 0, with nh = b — a the distribution tends to a uniform distribution over (a, b). The standard discrete rectangular distribution has a = 0 and h = 1/n so that X takes values 0, 1/n, 2/n,…, 1.
Fig. 55 An example of Dirichlet tessellation.
Discrete uniform distribution:
A probability distribution for a discrete random variable that takes on k distinct values xj, x2,…, xk with equal probabilities where k is a positive integer.
Discrete variables:
Variables having only integer values, for example, number of births, number of pregnancies, number of teeth extracted, etc.
Discrete wavelet transform (DWT):
The calculation of the coefficients of the wavelet series approximation for a discrete signal fj, f2,…, fn of finite extent. Essentially maps the vector f = {fj,f2,…,/n] to a vector of n wavelet transform coefficients.
Discriminant analysis:
A term that covers a large number of techniques for the analysis of multivariate data that have in common the aim to assess whether or not a set of variables distinguish or discriminate between two (or more) groups of individuals. In medicine, for example, such methods are generally applied to the problem of using optimally the results from a number of tests or the observations of a number of symptoms to make a diagnosis that can only be confirmed perhaps by post-mortem examination. In the two group case the most commonly used method is Fisher’s linear discriminant function, in which a linear function of the variables giving maximal separation between the groups is determined. This results in a classification rule (often also known as an allocation rule) that may be used to assign a new patient to one of the two groups. The derivation of this linear function assumes that the variance-covariance matrices of the two groups are the same. If they are not then a quadratic discriminant function may be necessary to distinguish between the groups. Such a function contains powers and cross-products of variables. The sample of observations from which the discriminant function is derived is often known as the training set. When more than two groups are involved (all with the same var-iance-covariance matrix) then it is possible to determine several linear functions of the variables for separating them. In general the number of such functions that can be derived is the smaller of q and g — J where q is the number of variables and g the number of groups. The collection of linear functions for discrimination are known as canonical discriminant functions or often simply as canonical variates. See also error rate estimation and regularised discriminant analysis. [MV2 Chapter 9.]
Discrimination information:
Synonymous with Kullback-Leibler information.
Disease clusters:
An unusual aggregation of health events, real or perceived. The events may be grouped in a particular area or in some short period of time, or they may occur among a certain group of people, for example, those having a particular occupation. The significance of studying such clusters as a means of determining the origins of public health problems has long been recognized. In J850, for example, the Broad Street pump in London was identified as a major source of cholera by plotting cases on a map and noting the cluster around the well. More recently, recognition of clusters of relatively rare kinds of pneumonia and tumours among young homosexual men led to the identification of acquired immunodeficiency syndrome (AIDS) and eventually to the discovery of the human immunodeficiency virus (HIV). See also scan statistic.
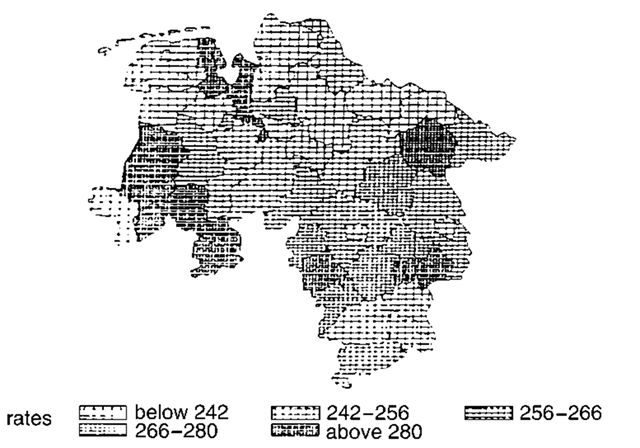
Disease mapping:
The process of displaying the geographical variability of disease on maps using different colours, shading, etc. The idea is not new, but the advent of computers and computer graphics has made it simpler to apply and it is now widely used in descriptive epidemiology, for example, to display morbidity or mortality information for an area. Figure 56 shows an example. Such mapping may involve absolute rates, relative rates, etc., and often the viewers impression of geographical variation in the data may vary quite markedly according to the methodology used. [Biometrics, 1995, 51, 1355-60.]
Dispersion:
The amount by which a set of observations deviate from their mean. When the values of a set of observations are close to their mean, the dispersion is less than when they are spread out widely from the mean. See also variance.
Dissimilarity coefficient:
A measure of the difference between two observations from (usually) a set of multivariate data. For two observations with identical variable values the dissimilarity is usually defined as zero. See also metric inequality.
Dissimilarity matrix:
A square matrix in which the elements on the main diagonal are zero, and the off-diagonal elements are dissimilarity coefficients of each pair of stimuli or objects of interest. Such matrices can either arise by calculations on the usual multivariate data matrix X or directly from experiments in which human subjects make judgements about the stimuli.
Distance sampling:
A method of sampling used in ecology for determining how many plants or animals are in a given fixed area. A set of randomly placed lines or points is established and distances measured to those objects detected by travelling the line or surveying the points. As a particular object is detected, its distance to the randomly chosen line or point is measured and on completion n objects have been detected and their associated distances recorded. Under certain assumptions unbiased estimates of density can be made from these distance data. See also line-intercept sampling.
Fig. 56 Disease mapping illustrated by age-standardized mortality rates in part of Germany.
Distributed database:
A database that consists of a number of component parts which are situated at geographically separate locations.
Distribution free methods:
Statistical techniques of estimation and inference that are based on a function of the sample observations, the probability distribution of which does not depend on a complete specification of the probability distribution of the population from which the sample was drawn. Consequently the techniques are valid under relatively general assumptions about the underlying population. Often such methods involve only the ranks of the observations rather than the observations themselves. Examples are Wilcoxon’s signed rank test and Friedman’s two way analysis of variance. In many cases these tests are only marginally less powerful than their analogues which assume a particular population distribution (usually a normal distribution), even when that assumption is true. Also commonly known as nonpara-metric methods although the terms are not completely synonymous.
Divide-by-total models:
Models for polytomous responses in which the probability of a particular category of the response is typically modelled as a multinomial logistic function.
Divisive clustering:
Cluster analysis procedures that begin with all individuals in a single cluster, which is then successively divided by maximizing some particular measure of the separation of the two resulting clusters. Rarely used in practice. See also agglom-erative hierarchical clustering methods and K-means cluster analysis.
Dixon test:
A test for outliers. When the sample size, n, is less than or equal to seven, the test statistic is
where y^ is the suspected outlier and is the smallest observation in the sample, y^) is the next smallest and y^ the largest observation. For n > 7, y^ is used instead of y^ and y(n_1) in place of y^. Critical values are available in some statistical tables. [Journal of Statistical Computation and Simulation, 1997, 58, 1-20.]
Doane’s rule:
A rule for calculating the number of classes to use when constructing a histogram and given by
where n is the sample size and y is an estimate of kurtosis. See also Sturges’ rule.
Dodge, Harold (1893-1976):
Born in the mill city of Lowell, Massachusetts, Dodge became one of the most important figures in the introduction of quality control and the development and introduction of acceptance sampling. He was the originator of the operating characteristic curve. Dodge’s career was mainly spent at Bell Laboratories, and his contributions were recognized with the Shewhart medal of the American Society for Quality Control in 1950 and an Honorary Fellowship of the Royal Statistical Society in 1975. He died on 10 December 1976 at Mountain Lakes, New Jersey.
Dodge’s continuous sampling plan:
A procedure for monitoring continuous production processes.
Doll, Sir Richard (1912-2005):
Born in Hampton, England, Richard Doll studied medicine at St. Thomas’s Hospital Medical School in London, graduating in 1937. From 1939 until 1945 he served in the Royal Army Medical Corps and in 1946 started work at the Medical Research Council. In 1951 Doll and Bradford Hill started a study that would eventually last for 50 years, asking all the doctors in Britain what they themselves smoked and then tracking them down over the years to see what they died of. The early results confirmed that smokers were much more likely to die of lung cancer than non-smokers, and the 10-year results showed that smoking killed far more people from other diseases than from lung cancer. The study has arguably helped to save millions of lives. In 1969 Doll was appointed Regius Professor of Medicine at Oxford and during the next ten years helped to develop one of the top medical schools in the world. He retired from administrative work in 1983 but continued his research, publishing the 50-year follow-up on the British Doctors’ Study when he was 91 years old, on the 50th anniversary of the first publication from the study. Doll received many honours during his distinguished career including an OBE in 1956, a knighthood in 1971, becoming a Companion of Honour in 1996, the UN award for cancer research in 1962 and the Royal Medal from the Royal Society in 1986. He also received honorary degrees from 13 universities. Doll died in Oxford on 24 July 2005, aged 92.
Doob-Meyer decomposition:
A theorem which shows that any counting process may be uniquely decomposed as the sum of a martingale and a predictable, right-continous process called the compensator, assuming certain mathematical conditions.
Doran estimator:
An estimator of the missing values in a time series for which monthly observations are available in a later period but only quarterly observations in an earlier period.
Dorfman-Berbaum-Metz method:
An approach to analysing multireader receiver operating characteristic curves data, that applies an analysis of variance to pseudovalues of the ROC parameters computed by jackknifing cases separately for each reader-treatment combination. See also Obuchowski and Rockette method.
Dorfman scheme:
An approach to investigations designed to identify a particular medical condition in a large population, usually by means of a blood test, that may result in a considerable saving in the number of tests carried out. Instead of testing each person separately, blood samples from, say, k people are pooled and analysed together. If the test is negative, this one test clears k people. If the test is positive then each of the k individual blood samples must be tested separately, and in all k + 1 tests are required for these k people. If the probability of a positive test (p) is small, the scheme is likely to result in far fewer tests being necessary. For example, if p = 0.01, it can be shown that the value of k that minimizes the expected number of tests per person is 11, and that the expected number of tests is 0.2, resulting in 80% saving in the number of tests compared with testing each individual separately. [Annals of Mathematical Statistics, 1943, 14, 436-40.]
Dose-ranging trial:
A clinical trial, usually undertaken at a late stage in the development of a drug, to obtain information about the appropriate magnitude of initial and subsequent doses. Most common is the parallel-dose design, in which one group of subjects in given a placebo, and other groups different doses of the active treatment. [Controlled Clinical Trials, 1995, 16, 319-30.]
Dose-response curve:
A plot of the values of a response variable against corresponding values of dose of drug received, or level of exposure endured, etc. See Fig. 57.
Dot plot:
A more effective display than a number of other methods, for example, pie charts and bar charts, for displaying quantitative data which are labelled. An example of such a plot showing standardized mortality rates (SMR) for lung cancer for a number of occupational groups is given in Fig. 58.
Double-centred matrices:
Matrices of numerical elements from which both row and column means have been subtracted. Such matrices occur in some forms of multidimensional scaling.
Double-count surveys:
Surveys in which two observers search the sampled area for the species of interest. The presence of the two observers permits the calculation of a survey-specific correction for visibility bias.
Fig. 57 A hypothetical dose-response curve.
Fig. 58 A dot plot giving standardized mortality rates for lung cancer for several occupational groups.
Double-dummy technique:
A technique used in clinical trials when it is possible to make an acceptable placebo for an active treatment but not to make two active treatments identical. In this instance, the patients can be asked to take two sets of tablets throughout the trial: one representing treatment A (active or placebo) and one treatment B (active or placebo). Particularly useful in a crossover trial.
Double-exponential distribution:
Synonym for Laplace distribution.
Double-masked:
Synonym for double-blind.
Double reciprocal plot:
Synonym for Lineweaver-Burke plot.
Double sampling:
A procedure in which initially a sample of subjects is selected for obtaining auxillary information only, and then a second sample is selected in which the variable of interest is observed in addition to the auxillary information. The second sample is often selected as a subsample of the first. The purpose of this type of sampling is to obtain better estimators by using the relationship between the auxillary variables and the variable of interest. See also two-phase sampling.
Doubly censored data:
Data involving survival times in which the time of the originating event and the failure event may both be censored observations. Such data can arise when the originating event is not directly observable but is detected via periodic screening studies. [Statistics in Medicine, 1992, 11, 1569-78.]
Doubly multivariate data:
A term sometimes used for the data collected in those longitudinal studies in which more than a single response variable is recorded for each subject on each occasion. For example, in a clinical trial, weight and blood pressure may be recorded for each patient on each planned visit.
Doubly ordered contingency tables:
Contingency tables in which both the row and column categories follow a natural order. An example might be, drug toxicity ranging from mild to severe, against drug dose grouped into a number of classes. A further example from a more esoteric area is shown.
| Cross-classification of whiskey for age and grade | ||
| Grade | ||
| Years/maturity | 1 | 2 3 |
| 7 | 4 | 2 0 |
| 5 | 2 | 2 2 |
| 1 | 0 | 0 4 |
Downton, Frank (1925-1984):
Downton studied mathematics at Imperial College London and after a succession of university teaching posts became Professor of Statistics at the University of Birmingham in 1970. Contributed to reliability theory and queue-ing theory. Downton died on 9 July 1984.
Dragstedt-Behrens estimator:
An estimator of the median effective dose in bioassay.
Draughtsman’s plot:
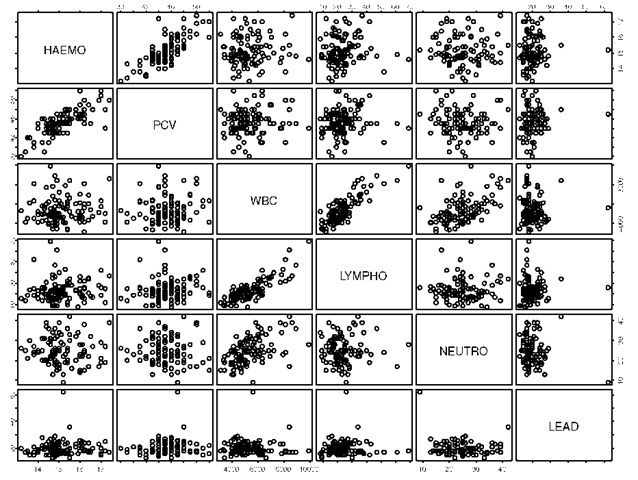
An arrangement of the pairwise scatter diagrams of the variables in a set of multivariate data in the form of a square grid. Such an arrangement may be extremely useful in the initial examination of the data. Each panel of the matrix is a scatter plot of one variable against another. The upper left-hand triangle of the matrix contains all pairs of scatterplots and so does the lower right-hand triangle. The reasons for including both the upper and lower triangles in the matrix, despite the seeming redundancy, is that it enables a row and column to be visually scanned to see one variable against all others, with the scales for the one variable lined up along the horizontal or the vertical. An example of such a plot is shown in Fig. 59. [Visualizing Data, 1993, W.S. Cleveland, Hobart Press, Summit, New Jersey.]
Drift:
A term used for the progressive change in assay results throughout an assay run.
Dropout:
A patient who withdraws from a study (usually a clinical trial) for whatever reason, noncompliance, adverse side effects, moving away from the district, etc. In many cases the reason may not be known. The fate of patients who drop out of an investigation must be determined whenever possible since the dropout mechanism may have implications for how data from the study should be analysed.
Drug stability studies:
Studies conducted in the pharmaceutical industry to measure the degradation of a new drug product or an old drug formulated or packaged in a new way. The main study objective is to estimate a drug’s shelf life, defined as the time point where the 95% lower confidence limit for the regression line crosses the lowest acceptable limit for drug content according to the Guidelines for Stability Testing.
Dual scaling:
Synonym for correspondence analysis.
Fig. 59 Draughtsman’s plot.
Dual system estimates:
Estimates which are based on a census and a post-enumeration survey, which try to overcome the problems that arise from the former in trying, but typically failing, to count everyone.
Dummy variables:
The variables resulting from recoding categorical variables with more than two categories into a series of binary variables. Marital status, for example, if originally labelled 1 for married, 2 for single and 3 for divorced, widowed or separated, could be redefined in terms of two variables as follows Variable 1: 1 if single, 0 otherwise;
Variable 2: 1 if divorced, widowed or separated, 0 otherwise; For a married person both new variables would be zero. In general a categorical variable with k categories would be recoded in terms of k — 1 dummy variables. Such recoding is used before polychotomous variables are used as explanatory variables in a regression analysis to avoid the unreasonable assumption that the original numerical codes for the categories, i.e. the values 1, 2,…, k, correspond to an interval scale.
Duncan’s test:
A modified form of the Newman-Keuls multiple comparison test.
Dunnett’s test:
A multiple comparison test intended for comparing each of a number of treatments with a single control.
Dunn’s test:
A multiple comparison test based on the Bonferroni correction.
Duration time:
The time that elapses before an epidemic ceases.
Durbin-Watson test:
A test that the residuals from a linear regression or multiple regression are independent. The test statistic is
where ri = yi — yi and yi and y i are, respectively, the observed and predicted values of the response variable for individual i. D becomes smaller as the serial correlations increase. Upper and lower critical values, Dv and DL have been tabulated for different values of q (the number of explanatory variables) and n. If the observed value of D lies between these limits then the test is inconclusive.
Dutch topic:
A gamble that gives rise to certain loss, no matter what actually occurs. Used as a rhetorical device in subjective probability and Bayesian statistics.
Dynamic allocation indices:
Indices that give a priority for each project in a situation where it is necessary to optimize in a sequential manner the allocation of effort between a number of competing projects. The indices may change as more effort is allocated.
Dynamic graphics:
Computer graphics for the exploration of multivariate data which allow the observations to be rotated and viewed from all directions. Particular sets of observations can be highlighted. Often useful for discovering structure or pattern, for example, the presence of clusters. See also brushing scatterplots. [Dynamic Graphics for Statistics, 1987, W.S. Cleveland and M.E. McGill, Wadsworth, Belmont, California.]