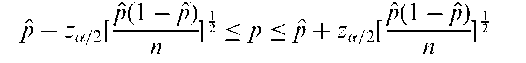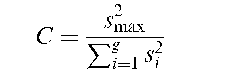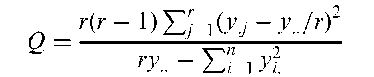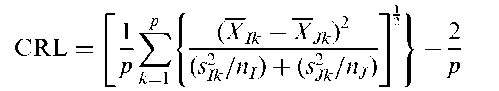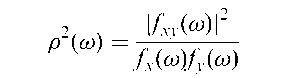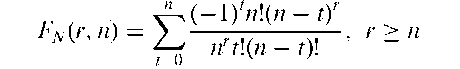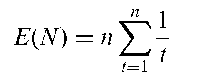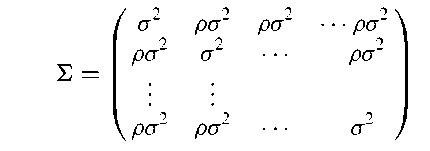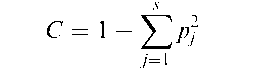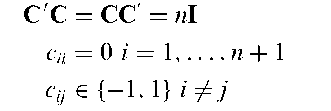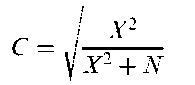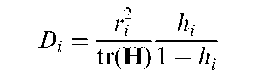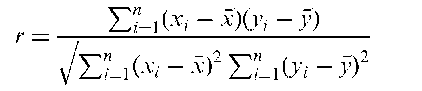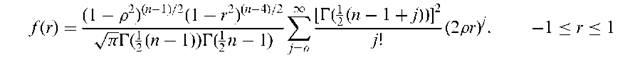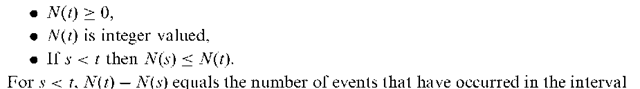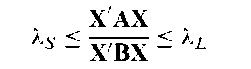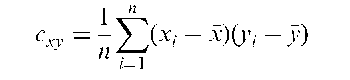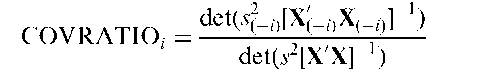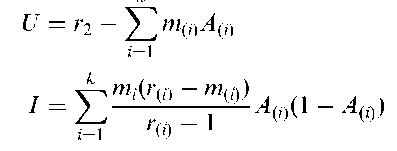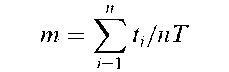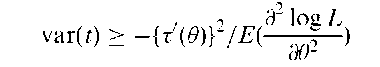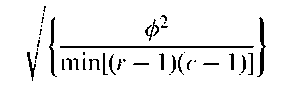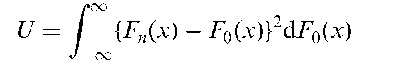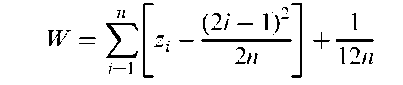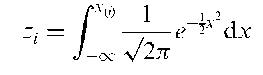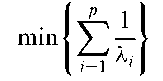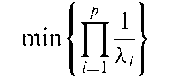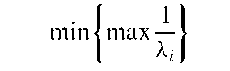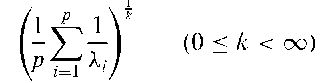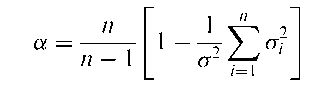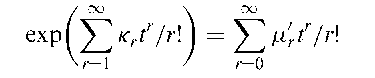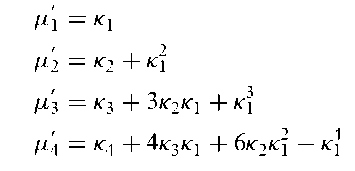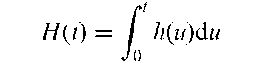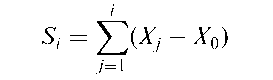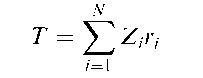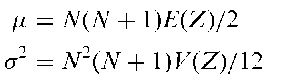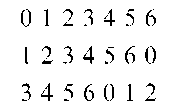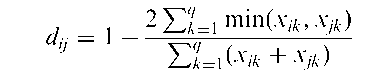Clinical trial:
A prospective study involving human subjects designed to determine the effectiveness of a treatment, a surgical procedure, or a therapeutic regimen administered to patients with a specific disease. See also phase I trials, phase II trials and phase III trials.
Clinical vs statistical significance:
The distinction between results in terms of their possible clinical importance rather than simply in terms of their statistical significance. With large samples, for example, very small differences that have little or no clinical importance may turn out to be statistically significant. The practical implications of any finding in a medical investigation must be judged on clinical as well as statistical grounds.
Clopper-Pearson interval:
A confidence interval for the probability of success in a series of n independent repeated Bernoulli trials. For large sample sizes a 100(1— a/2)% interval is given by
where za=2 is the appropriate standard normal deviate and p = B/n where B is the observed number of successes. See also binomial test.
ClustanGraphics:
A specialized software package that contains advanced graphical facilities for cluster analysis.
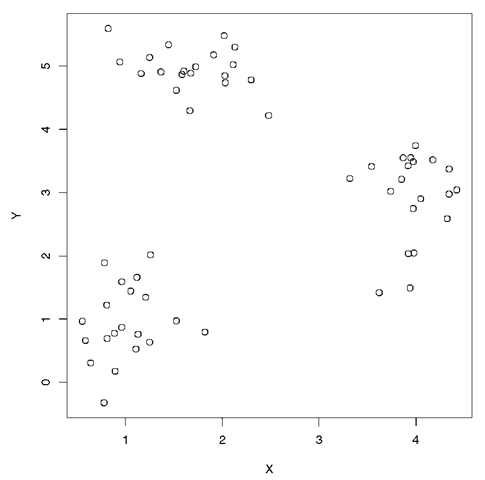
Cluster analysis:
A set of methods for constructing a (hopefully) sensible and informative classification of an initially unclassified set of data, using the variable values observed on each individual. Essentially all such methods try to imitate what the eye-brain system does so well in two dimensions; in the scatterplot shown at Fig. 37, for example, it is very simple to detect the presence of three clusters without making the meaning of the term ‘ cluster’ explicit. See also agglomerative hierarchical clustering, K-means clustering, and finite mixture densities.
Clustered data:
A term applied to both data in which the sampling units are grouped into clusters sharing some common feature, for example, animal litters, families or geographical regions, and longitudinal data in which a cluster is defined by a set of repeated measures on the same unit. A distinguishing feature of such data is that they tend to exhibit intracluster correlation, and their analysis needs to address this correlation to reach valid conclusions. Methods of analysis that ignore the correlations tend to be inadequate. In particular they are likely to give estimates of standard errors that are too low. When the observations have a normal distribution, random effects models and mixed effects models may be used. When the observations are binary, giving rise to clustered binary data, suitable methods are mixed-effects logistic regression and the generalized estimating equation approach. See also multilevel models.
Cluster randomization:
The random allocation of groups or clusters of individuals in the formation of treatment groups. Although not as statistically efficient as individual randomization, the procedure frequently offers important economic, feasibility or ethical advantages. Analysis of the resulting data may need to account for possible intracluster correlation (see clustered data).
Cluster sampling:
A method of sampling in which the members of a population are arranged in groups (the ‘clusters’). A number of clusters are selected at random and those chosen are then subsampled. The clusters generally consist of natural groupings, for example, families, hospitals, schools, etc. See also random sample, area sampling, stratified random sampling and quota sample.
Cluster-specific models:
Synonym for subject-specific models.
Cmax:
A measure traditionally used to compare treatments in bioequivalence trials. The measure is simply the highest recorded response value for a subject. See also area under curve, response feature analysis and Tmax.
Coale-Trussell fertility model:
A model used to describe the variation in the age pattern of human fertility, which is given by Rla = naM,em’v- where Ria is the expected marital fertility rate, for the ath age of the ith population, na is the standard age pattern of natural fertility, va is the typical age-specific deviation of controlled fertility from natural fertility, and Mi and mi measure the ith population’s fertility level and control. The model states that marital fertility is the product of natural fertility, naMt, and fertility control, exp(m;va)
Coarse data:
A term sometimes used when data are neither entirely missing nor perfectly present. A common situation where this occurs is when the data are subject to rounding; others correspond to digit preference and age heaping.
Cobb-Douglas distribution:
A name often used in the economics literature as an alternative for the lognormal distribution.
Cochrane, Archibald Leman (1909-1988):
Cochrane studied natural sciences in Cambridge and psychoanalysis in Vienna. In the 1940s he entered the field of epidemiology and then later became an enthusiastic advocate of clinical trials. His greatest contribution to medical research was to motivate the Cochrane collaboration. Cochrane died on 18 June 1988 in Dorset in the United Kingdom.
Cochrane collaboration:
An international network of individuals committed to preparing , maintaining and disseminating systematic reviews of the effects of health care. The collaboration is guided by six principles: collaboration, building on people’s existing enthusiasm and interests, minimizing unnecessary duplication, avoiding bias, keeping evidence up to data and ensuring access to the evidence. Most concerned with the evidence from randomized clinical trials. See also evidence-based medicine.
Cochrane-Orcutt procedure:
A method for obtaining parameter estimates for a regression model in which the error terms follow an autoregressive model of order one, i.e. a model
where vt = avt—1 + et and yt are the dependent values measured at time t, xt is a vector of explanatory variables, b is a vector of regression coefficients and the et are assumed independent normally distributed variables with mean zero and variance a2. Writing y* = yt — ayt—1 and x* = xt — axt—1 an estimate of b can be obtained from ordinary least squares of y* and x*. The unknown parameter a can be calculated from the residuals from the regression, leading to an iterative process in which a new set of transformed variables are calculated and thus a new set of regression estimates and so on until convergence. [Communications in Statistics, 1993, 22, 1315-33.]
Cochran’s C-test:
A test that the variances of a number of populations are equal. The test statistic is
where g is the number of populations and st, i = 1,…, g are the variances of samples from each, of which s^iax is the largest. Tables of critical values are available. See also Bartlett’s test, Box’s test and Hartley’s test.
Cochran’s Q-test:
A procedure for assessing the hypothesis of no inter-observer bias in situations where a number of raters judge the presence or absence of some characteristic on a number of subjects. Essentially a generalized McNemar’s test. The test statistic is given by
where y^ = 1 if the ith patient is judged by the jth rater to have the characteristic present and 0 otherwise, y: is the total number of raters who judge the ith subject to have the characteristic, y j is the total number of subjects the jth rater judges as having the characteristic present, y is the total number of ‘present’ judgements made, n is the number of subjects and r the number of raters. If the hypothesis of no inter-observer bias is true, Q, has approximately, a chi-squared distribution with r — 1 degrees of freedom.
Cochran’s Theorem:
Let x be a vector of q independent standardized normal variables and let the sum of squares Q = x’x be decomposed into k quadratic forms Q,- = x’Aj-x with ranks ri, i.e.
Then any one of the following three conditions implies the other two;
• The ranks ri of the Q, add to that of Q.
• Each of the Q, has a chi-squared distribution.
• Each Qi is independent of every other.
Cochran, William Gemmell (1909-1980):
Born in Rutherglen, a surburb of Glasgow, Cochran read mathematics at Glasgow University and in 1931 went to Cambridge to study statistics for a Ph.D. While at Cambridge he published what was later to become known as Cochran’s Theorem. Joined Rothamsted in 1934 where he worked with Frank Yates on various aspects of experimental design and sampling. Moved to the Iowa State College of Agriculture, Ames in 1939 where he continued to apply sound experimental techniques in agriculture and biology. In 1950, in collaboration with Gertrude Cox, published what quickly became the standard text topic on experimental design, Experimental Designs. Became head of the Department of Statistics at Harvard in 1957, from where he eventually retired in 1976. President of the Biometric Society in 1954-1955 and Vice-president of the American Association for the Advancement of Science in 1966. Cochran died on 29 March 1980 in Orleans, Massachusetts.
Codominance:
The relationship between the genotype at a locus and a phenotype that it influences. If individuals with heterozygote (for example, AB) genotype is phenoty-pically different from individuals with either homozygous genotypes (AA and BB), then the genotype-phenotype relationship is said to be codominant.
Coefficient of alienation:
A name sometimes used for 1 — r2, where r is the estimated value of the correlation coefficient of two random variables. See also coefficient of determination.
Coefficient of concordance:
A coefficient used to assess the agreement among m raters ranking n individuals according to some specific characteristic. Calculated as
where S is the sum of squares of the differences between the total of the ranks assigned to each individual and the value m(n + 1)/2. W can vary from 0 to 1 with the value 1 indicating perfect agreement.
Coefficient of determination:
The square of the correlation coefficient between two variables. Gives the proportion of the variation in one variable that is accounted for by the other.
Coefficient of racial likeness (CRL):
Developed by Karl Pearson for measuring resemblances between two samples of skulls of various origins. The coefficient is defined for two samples I and J as:
where XIk stands for the sample mean of the kth variable for sample I and stands for the variance of this variable. The number of variables is p.
Coefficient of variation:
A measure of spread for a set of data defined as 100 x standard deviation/mean Originally proposed as a way of comparing the variability in different distributions, but found to be sensitive to errors in the mean.
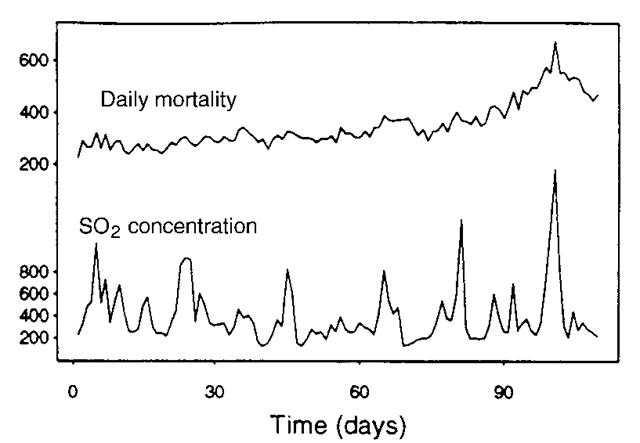
Coherence:
A term most commonly used in respect of the strength of association of two time series. Figure 38, for example, shows daily mortality and SO2 concentration time series in London during the winter months of 1958, with an obvious question as to
Fig. 38 Time series for daily mortality and sulphur dioxide concentration in London during the winter months of 1958.
whether the pollution was in any way affecting mortality. The relationship is usually measured by the time series analogue of the correlation coefficient, although the association structure is likely to be more complex and may include a leading or lagging relationship; the measure is no longer a single number but a function, p{!), of frequency !. Defined explicitly in terms of the Fourier transforms fx(!), fyd and fxy(!) of the autocovariance functions of Xt and Yt and their cross-covariance function as
The squared coherence is the proportion of variability of the component of Yt with frequency ! explained by the corresponding Xt component. This corresponds to the interpretation of the squared multiple correlation coefficient in multiple regression.
Cohort component method:
A widely used method of forecasting the age- and sex-specific population to future years, in which the initial population is stratified by age and sex and projections are generated by application of survival ratios and birth rates, followed by an additive adjustment for net migration. The method is widely used because it provides detailed information on an area’s future population, births, deaths, and migrants by age, sex and race, information that is uesful for many areas of planning and public administration.
Cohort study:
An investigation in which a group of individuals (the cohort) is identified and followed prospectively, perhaps for many years, and their subsequent medical history recorded. The cohort may be subdivided at the onset into groups with different characteristics, for example, exposed and not exposed to some risk factor, and at some later stage a comparison made of the incidence of a particular disease in each group. See also prospective study.
Coincidences:
Surprising concurrence of events, perceived as meaningfully related, with no apparent causal connection. Such events abound in everyday life and are often the source of some amazement. As pointed out by Fisher, however, ‘the one chance in a million will undoubtedly occur, with no less and no more than its appropriate frequency, however surprised we may be that it should occur to us’.
Collapsing categories:
A procedure often applied to contingency tables in which two or more row or column categories are combined, in many cases so as to yield a reduced table in which there are a larger number of observations in particular cells. Not to be recommended in general since it can lead to misleading conclusions. See also Simpson’s paradox.
Collector’s problem:
A problem that derives from schemes in which packets of a particular brand of tea, cereal etc., are sold with cards, coupons or other tokens. There are say n different cards that make up a complete set, each packet is sold with one card, and a priori this card is equally likely to be any one of the n cards in the set. Of principal interest is the distribution of N, the number of packets that a typical customer must buy to obtain a complete set. It can be shown that the cumulative probability distribution of N, Fn(r, n) is given by
The expected value of N is
Collinearity:
Synonym for multicollinearity.
Collision test:
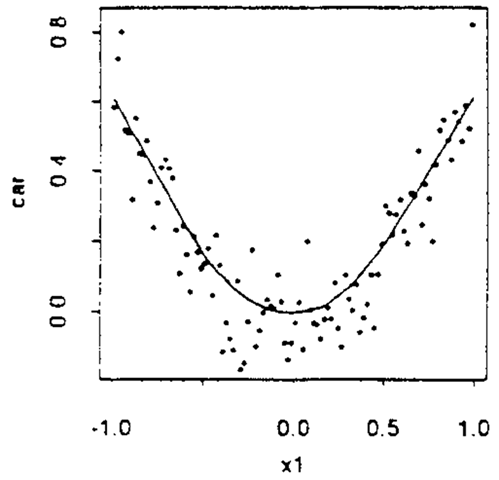
A test for randomness in a sequence of digits.Combining conditional expectations and residuals plot (CERES): A generalization of the partial residual plot which is often useful in assessing whether a multiple regression in which each explanatory variable enters linearly is valid. It might, for example, be suspected that for one of the explanatory variables, x,-, an additional square or square root term is needed. To make the plot the regression model is estimated, the terms involving functions of x, are added to the residuals and the result is plotted against x,. An example is shown in Fig. 39.
Commensurate variables:
Variables that are on the same scale or expressed in the same units, for example, systolic and diastolic blood pressure.
Common factor variance:
A term used in factor analysis for that part of the variance of a variable shared with the other observed variables via the relationships of these variable to the common factors.
Common principal components analysis:
A generalization of principal components analysis to several groups. The model for this form of analysis assumes that the variance-covariance matrices, of k populations have identical eigenvectors, so that the same orthogonal matrix diagonalizes all simultaneously. A modification of the model, partial common principal components, assumes that only r out of q eigenvectors are common to all while the remaining q — r eigenvectors are specific in each group.
Fig. 39 An example of a CERES plot.
Communality:
Synonym for common factor variance.
Community intervention study:
An intervention study in which the experimental unit to be randomized to different treatments is not an individual patient or subject but a group of people, for example, a school, or a factory. See also cluster randomization.
Co-morbidity:
The potential co-occurrence of two disorders in the same individual, family etc.
Comparative calibration:
The statistical methodology used to assess the calibration of a number of instruments, each designed to measure the same characteristic on a common group of individuals. Unlike a normal calibration exercise, the true underlying quantity measured is unobservable.
Comparative exposure rate:
A measure of association for use in a matched case-control study, defined as the ratio of the number of case-control pairs, where the case has greater exposure to the risk factor under investigation, to the number where the control has greater exposure. In simple cases the measure is equivalent to the odds ratio or a weighted combination of odds ratios. In more general cases the measure can be used to assess association when an odds ratio computation is not feasible.
Comparative trial:
Synonym for controlled trial.
Comparison group:
Synonym for control group.
Comparison wise error rate:
Synonym for per-comparison error rate.
Compartment models:
Models for the concentration or level of material of interest over time. A simple example is the washout model or one compartment model given by
where Y(t) is the concentration at time t > 00
Compensatory equalization:
A process applied in some clinical trials and intervention studies, in which comparison groups not given the perceived preferred treatment are provided with compensations that make these comparison groups more equal than originally planned.
Competing risks:
A term used particularly in survival analysis to indicate that the event of interest (for example, death), may occur from more than one cause. For example, in a study of smoking as a risk factor for lung cancer, a subject who dies of coronary heart disease is no longer at risk of lung cancer. Consequently coronary heart disease is a competing risk in this situation.
Compiler average causal effect (CACE):
The treatment effect among true compilers in a clinical trial. For a suitable response variable, the CACE is given by the mean difference in outcome between compliers in the treatment group and those controls who would have complied with treatment had they been randomized to the treatment group. The CACE may be viewed as a measure of ‘efficacy’ as opposed to ‘effectiveness’.
Complementary events:
Mutually exclusive events A and B for which
Pr(A) + Pr(B) = 1
where Pr denotes probability.
Complementary log-log transformation:
A transformation of a proportion, p, that is often a useful alternative to the logistic transformation. It is given by
y = ln[— ln(1 - p)]
This function transforms a probability in the range (0,1) to a value in (—1,1), but unlike the logistic and probit transformation it is not symmetric about the value p = 0.5. In the context of a bioassay, this transformation can be derived by supposing that the tolerances of individuals have the Gumbel distribution. Very similar to the logistic transformation when p is small.
Complete case analysis:
An analysis that uses only individuals who have a complete set of measurements. An individual with one or more missing values is not included in the analysis. When there are many individuals with missing values this approach can reduce the effective sample size considerably. In some circumstances ignoring the individuals with missing values can bias an analysis. See also available case analysis and missing values.
Complete ennumeration:
Synonym for census.
Complete estimator:
A weighted combination of two (or more) component estimators.
Mainly used in sample survey work.
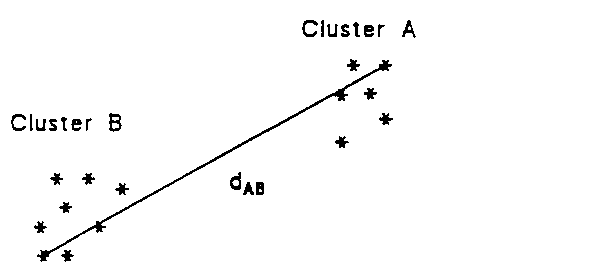
Complete linkage cluster analysis:
An agglomerative hierarchical clustering method in which the distance between two clusters is defined as the greatest distance between a member of one cluster and a member of the other. The between group distance measure used is illustrated in Fig. 40.
Completely randomized design:
An experimental design in which the treatments are allocated to the experimental units purely on a chance basis.
Completeness:
A term applied to a statistic t when there is only one function of that statistic that can have a given expected value. If, for example, the one function of t is an unbiased estimator of a certain function of a parameter, 6, no other function of t will be. The concept confers a uniqueness property upon an estimator.
Complete spatial randomness:
A Poisson process in the plane for which:
• the number of events N(A) in any region A follows a Poisson distribution with mean k\A\;
• given N(A) = n, the events in A form an independent random sample from the uniform distribution on A.
Here \ A\ denotes the area of A, and k is the mean number of events per unit area. Often used as the standard against which to compare an observed spatial pattern.
Compliance:
The extent to which patients in a clinical trial follow the trial protocol. [SMR Chapter 15.]
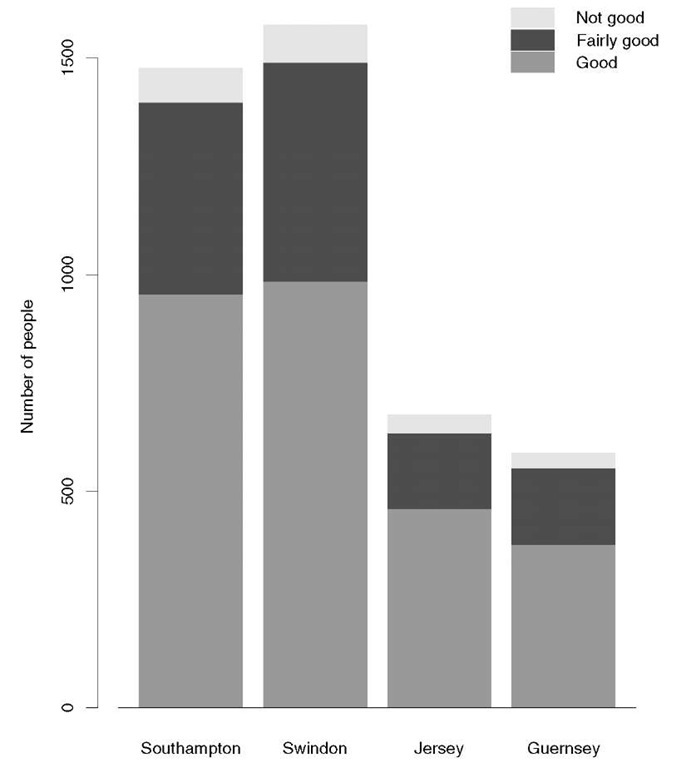
Component bar chart:
A bar chart that shows the component parts of the aggregate represented by the total length of the bar. The component parts are shown as sectors of the bar with lengths in proportion to their relative size. Shading or colour can be used to enhance the display. Figure 41 gives an example.
Component-plus-residual plot:
Synonym for partial-residual plot.
Composite estimators:
Estimators that are a weighted combination of two or more component estimators. Often used in sample survey work.
Composite hypothesis:
A hypothesis that specifies more than a single value for a parameter.
For example, the hypothesis that the mean of a population is greater than some value.
Fig. 40 Complete linkage distance for two clusters A and B.
Fig. 41 Component bar chart showing subjective health assessment in four regions.
Composite sampling:
A procedure whereby a collection of multiple sample units are combined in their entirety or in part, to form a new sample. One or more subsequent measurements are taken on the combined sample, and the information on the sample units is lost. An example is Dorfman’s scheme. Because composite samples mask the respondent’s identity their use may improve rates of test participation in senstive areas such as testing for HIV. [Technometrics, 1980, 22, 179-86.]
Compositional data:
A set of observations, x1, x2,…, xn for which each element of x,- is a proportion and the elements of x, are constrained to sum to one. For example, a number of blood samples might be analysed and the proportion, in each, of a number of chemical elements recorded. Or, in geology, percentage weight composition of rock samples in terms of constituent oxides might be recorded. The appropriate sample space for such data is a simplex and much of the analysis of this type of data involves the Dirichlet distribution.
Compound binomial distribution:
Synonym for beta binomial distribution
Compound distribution:
A type of probability distribution arising when a parameter of a distribution is itself a random variable with a corresponding probability distribution. See, for example, beta-binomial distribution. See also contagious distribution.
Compound symmetry:
The property possessed by a variance-covariance matrix of a set of multivariate data when its main diagonal elements are equal to one another, and additionally its off-diagonal elements are also equal. Consequently the matrix has the general form;
where p is the assumed common correlation coefficient of the measures. Of most importance in the analysis of longitudinal data since it is the correlation structure assumed by the simple mixed-model often used to analyse such data. See also Mauchly test.
Computational complexity:
The number of operations of the predominant type in an algorithm. Investigations of how computational complexity increases with the size of a problem are important in keeping computational time to a minimum.
Computer algebra:
Computer packages that permit programming using mathematical expressions. See also Maple.
Computer-aided diagnosis:
Computer programs designed to support clinical decision making. In general, such systems are based on the repeated application of Bayes’ theorem. In some cases a reasoning strategy is implemented that enables the programs to conduct clinically pertinent dialogue and explain their decisions. Such programs have been developed in a variety of diagnostic areas, for example, the diagnosis of dyspepsia and of acute abdominal pain. See also expert system.
Computer-assisted interviews:
A method of interviewing subjects in which the interviewer reads the question from a computer screen instead of a printed page, and uses the keyboard to enter the answer. Skip patterns (i.e. ‘if so-and-so, go to Question such-and-such’) are built into the program, so that the screen automatically displays the appropriate question. Checks can be built in and an immediate warning given if a reply lies outside an acceptable range or is inconsistent with previous replies; revision of previous replies is permitted, with automatic return to the current question. The responses are entered directly on to the computer record, avoiding the need for subsequent coding and data entry. The program can make automatic selection of subjects who require additional procedures, such as special tests, supplementary questionnaires, or follow-up visits.
Computer-intensive methods:
Statistical methods that require almost identical computations on the data repeated many, many times. The term computer intensive is, of course, a relative quality and often the required ‘intensive’ computations may take only a few seconds or minutes on even a small PC. An example of such an approach is the bootstrap. See also jackknife.
Computer virus:
A computer program designed to sabotage by carrying out unwanted and often damaging operations. Viruses can be transmitted via disks or over networks. A number of procedures are available that provide protection against the problem.
Concentration matrix:
A term sometimes used for the inverse of the variance-covariance matrix of a multivariate normal distribution.
Concentration measure:
A measure, C, of the dispersion of a categorical random variable, Y, that assumes the integral values j, 1 < j < s with probability pj, given by
Concomitant variables:
Synonym for covariates.
Conditional distribution:
The probability distribution of a random variable (or the joint distribution of several variables) when the values of one or more other random variables are held fixed. For example, in a bivariate normal distribution for random variables X and Y the conditional distribution of Y given X is normal with mean fi2 + pa2a—1 (x — and variance &2> (1 — p2).
Conditional independence graph:
An undirected graph constructed so that if two variables, U and V, are connected only via a third variable W, then U and V are conditionally independent given W. An example is given in Fig. 42.
Conditional likelihood:
The likelihood of the data given the sufficient statistics for a set of nuisance parameters. [GLM Chapter 4.]
Conditional logistic regression:
Synonym for mixed effects logistic regression.
Conditional mortality rate:
Synonym for hazard function.
Conditional probability:
The probability that an event occurs given the outcome of some other event. Usually written, Pr(A\B). For example, the probability of a person being colour blind given that the person is male is about 0.1, and the corresponding probability given that the person is female is approximately 0.0001. It is not, of course, necessary that Pr(A|B) = Pr(B\A); the probability of having spots given that a patient has measles, for example, is very high, the probability of measles given that a patient has spots is, however, much less. If Pr(A\B) = Pr(A) then the events A and B are said to be independent. See also Bayes’ Theorem.
Condition number:
The ratio of the largest eigenvalue to the smallest eigenvalue of a matrix.
Provides a measure of the sensitivity of the solution from a regression analysis to small changes in either the explanatory variables or the response variable. A large
Fig. 42 An example of a conditional independence graph.
value indicates possible problems with the solution caused perhaps by collinearity. [ARA Chapter 10.]
Conference matrix:
An (n + 1)x(n + 1) matrix C satisfying
The name derives from an application to telephone conference networks.
Confidence interval:
A range of values, calculated from the sample observations, that is believed, with a particular probability, to contain the true parameter value. A 95% confidence interval, for example, implies that were the estimation process repeated again and again, then 95% of the calculated intervals would be expected to contain the true parameter value. Note that the stated probability level refers to properties of the interval and not to the parameter itself which is not considered a random variable (although see, Bayesian inference and Bayesian confidence interval). [KA2 Chapter 20.]
Confirmatory data analysis:
A term often used for model fitting and inferential statistical procedures to distinguish them from the methods of exploratory data analysis.
Confounding:
A process observed in some factorial designs in which it is impossible to differentiate between some main effects or interactions, on the basis of the particular design used. In essence the contrast that measures one of the effects is exactly the same as the contrast that measures the other. The two effects are usually referred to as aliases.
Confusion matrix:
Synonym for misclassification matrix.
Congruential methods:
Methods for generating random numbers based on a fundamental congruence relationship, which may be expressed as the following recursive formula
where ni, a, c and m are all non-negative integers. Given an initial starting value n0, a constant multiplier a, and an additive constant c then the equation above yields a congruence relationship (modulo m) for any value for i over the sequence {n1, n2,…, ni,…}. From the integers in the sequence {ni}, rational numbers in the unit interval (0, 1) can be obtained by forming the sequence {ri} = {n=m}. Frequency tests and serial tests, as well as other tests of randomness, when applied to sequences generated by the method indicate that the numbers are uncorrelated and uniformly distributed, but although its statistical behaviour is generally good, in a few cases it is completely unacceptable.
Conjoint analysis:
A method used primarily in market reasearch which is similar in many respects to multidimensional scaling. The method attempts to assign values to the levels of each attribute, so that the resulting values attached to the stimuli match, as closely as possible, the input evaluations provided by the respondents.
Conjugate prior:
A prior distribution for samples from a particular probability distribution such that the posterior distribution at each stage of sampling is of the same family, regardless of the values observed in the sample. For example, the family of beta distributions is conjugate for samples from a binomial distribution, and the family of gamma distributions is conjugate for samples from the exponential distribution.
Conover test:
A distribution free method for the equality of variance of two populations that can be used when the populations have different location parameters. The asymptotic relative efficiency of the test compared to the F-test for normal distributions is 76% . See also Ansari-Bradley test and Klotz test.
Conservative and non-conservative tests:
Terms usually encountered in discussions of multiple comparison tests. Non-conservative tests provide poor control over the per-experiment error rate. Conservative tests on the other hand, may limit the per-com-parison error rate to unecessarily low values, and tend to have low power unless the sample size is large.
Consistency:
A term used for a particular property of an estimator, namely that its bias tends to zero as sample size increases.
Consistency checks:
Checks built into the collection of a set of observations to assess their internal consistency. For example, data on age might be collected directly and also by asking about date of birth.
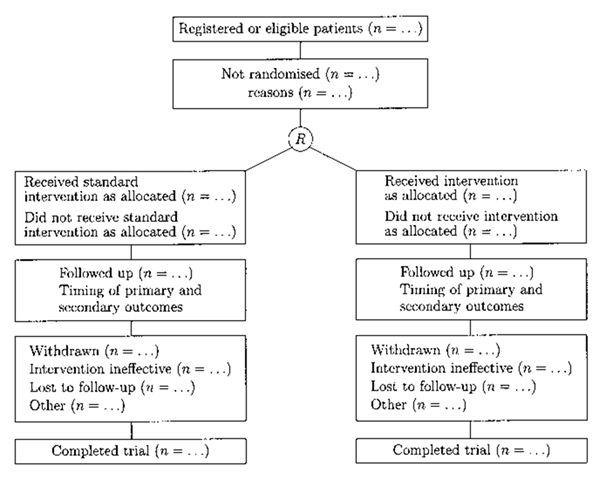
Consolidated Standards for Reporting Trials (CONSORT) statement:
A protocol for reporting the results of clinical trials. The core contribution of the statement consists of a flow diagram (see Fig. 43) and a checklist. The flow diagram enables reviewers and readers to quickly grasp how many eligible participants were randomly assigned to each arm of the trial. [Journal of the American Medical Association, 1996, 276, 637-9.]
Fig. 43 Consolidated standards for reporting trials.
Consumer price index (CPI):
A measure of the changes in prices paid by urban consumers for the goods and services they purchase. Essentially, it measures the purchasing power of consumers’ money by comparing what a sample or ‘market basket’ of goods and services costs today with what the same goods would have cost at an earlier date.
Contagious distribution:
A term used for the probability distribution of the sum of a number (N) of random variables, particularly when N is also a random variable. For example, if X1, X2,…, XN are variables with a Bernoulli distribution and N is a variable having a Poisson distribution with mean X, then the sum SN given by
can be shown to have a Poisson distribution with mean Xp where p = Pr(X,- = 1).
Contaminated normal distribution:
A term sometimes used for a finite mixture distribution of two normal distributions with the same mean but different variances. Such distributions have often been used in Monte Carlo studies. [Transformation and Weighting in Regression, 1988, R.J. Carroll and D. Ruppert, Chapman and Hall/ CRC Press, London.]
Contingency coefficient:
A measure of association, C, of the two variables forming a two-dimensional contingency table, given by
where X2 is the usual chi-squared statistic for testing the independence of the two variables and N is the sample size. See also phi-coefficient, Sakoda coefficient and Tschuprov coefficient.
Contingency tables:
The tables arising when observations on a number of categorical variables are cross-classified. Entries in each cell are the number of individuals with the corresponding combination of variable values. Most common are two-dimensional tables involving two categorical variables, an example of which is shown below.
| Retarded activity amongst psychiatric patients | |||
| Affectives | Schizo | Neurotics | Total |
| Retarded activity 12 | 13 | 5 | 30 |
| No retarded activity 18 | 17 | 25 | 60 |
| Total 30 | 30 | 30 | 90 |
The analysis of such two-dimensional tables generally involves testing for the independence of the two variables using the familiar chi-squared statistic. Three- and higher-dimensional tables are now routinely analysed using log-linear models.
Continual reassessment method:
An approach that applies Bayesian inference to determining the maximum tolerated dose in a phase Itrial. The method begins by assuming a logistic regression model for the dose-toxicity relationship and a prior distribution for the parameters. After each patient’s toxicity result becomes available the posterior distribution of the parameters is recomputed and used to estimate the probability of toxicity at each of a series of dose levels.
Continuous proportion:
Proportions of a continuum such as time or volume; for example, proportions of time spent in different conditions by a subject, or the proportions of different minerals in an ore deposit.
Continuous variable:
A measurement not restricted to particular values except in so far as this is constrained by the accuracy of the measuring instrument. Common examples include weight, height, temperature, and blood pressure. For such a variable equal sized differences on different parts of the scale are equivalent. See also categorical variable, discrete variable and ordinal variable.
Continuum regression:
Regression of a response variable, y, on that linear combination tY of explanatory variables which maximizes r2(y, t)var(t)y. The parameter y is usually chosen by cross-validated optimization over the predictors b’yx. Introduced as an alternative to ordinaryleast squares to deal with situations in which the explanatory variables are nearly collinear, the method trades variance for bias. See also principal components regression, partial least squares and ridge regression.
Contour plot:
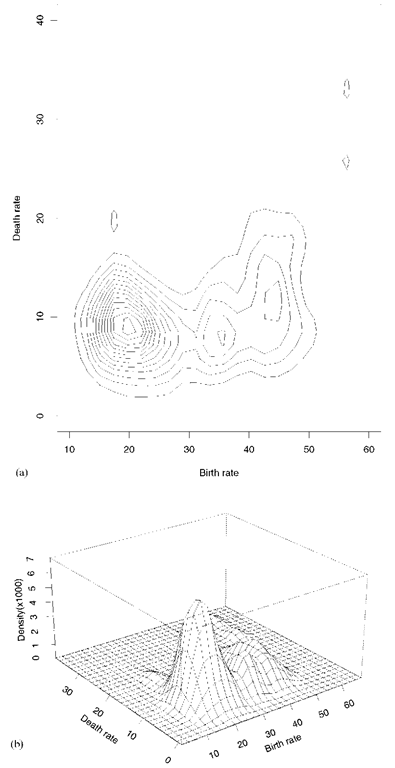
A topographical map drawn from data involving observations on three variables. One variable is represented on the horizontal axis and a second variable is represented on the vertical axis. The third variable is represented by isolines (lines of constant value). These plots are often helpful in data analysis, especially when searching for maxima or minima in such data. The plots are most often used to display graphically bivariate distributions in which case the third variable is value of the probability density function corresponding to the values of the two variables. An alternative method of displaying the same material is provided by the perspective plot in which the values on the third variable are represented by a series of lines constructed to give a three-dimensional view of the data. Figure 44 gives examples of these plots using birth and death rate data from a number of countries with a kernel density estimator used to calculate the bivariate distribution.
Contrast:
A linear function of parameters or statistics in which the coefficients sum to zero.
Most often encountered in the context of analysis of variance, in which the coefficients sum to zero. For example, in an application involving say three treatment groups (with means xT1, xT2 and xT3) and a control group (with mean xC), the following is the contrast for comparing the mean of the control group to the average of the treatment groups;
Fig. 44 Contour (a) and perspective (b) plots of estimated bivariate density function for birth and death rates in a number of countries.
Control group:
In experimental studies, a collection of individuals to which the experimental procedure of interest is not applied. In observational studies, most often used for a collection of individuals not subjected to the risk factor under investigation. In many medical studies the controls are drawn from the same clinical source as the cases to ensure that they represent the same catchment population and are subject to the same selective factors. These would be termed, hospital controls. An alternative is to use controls taken from the population from which the cases are drawn (community controls). The latter is suitable only if the source population is well defined and the cases are representative of the cases in this population.
Controlled trial:
A Phase III clinical trial in which an experimental treatment is compared with a control treatment, the latter being either the current standard treatment or a placebo.
Control statistics:
Statistics calculated from sample values x1, x2,…, xn which elicit information about some characteristic of a process which is being monitored. The sample mean, for example, is often used to monitor the mean level of a process, and the sample variance its imprecision. See also cusum and quality control procedures.
Convenience sample:
A non-random sample chosen because it is easy to collect, for example, people who walk by in the street. Such a sample is unlikely to be representative of the population of interest.
Convergence in probability:
Convergence of the probability of a sequence of random variables to a value.
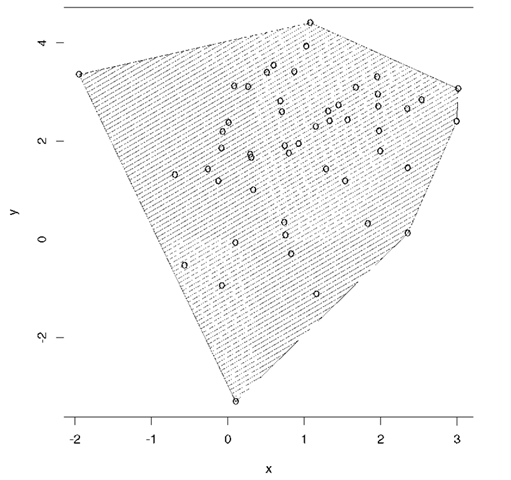
Convex hull:
The vertices of the smallest convex polyhedron in variable space within or on which all the data points lie. An example is shown in Fig. 45.
Convex hull trimming:
A procedure that can be applied to a set of bivariate data to allow robust estimation of Pearson’s product moment correlation coefficient. The points defining the convex hullof the observations, are deleted before the correlation coefficient is calculated. The major attraction of this method is that it eliminates isolated outliers without disturbing the general shape of the bivariate distribution.
Convolution:
An integral (or sum) used to obtain the probability distribution of the sum of two or more random variables.
Conway-Maxwell-Poisson distribution:
A generalization of the Poisson distribution, that has thicker or thinner tails than the Poisson distribution, which is included as a special case. The distribution is defined over positive integers and is flexible in representing a variety of shapes and in modelling overdispersion. [The Journal of Industrial Engineering, 1961, 12, 32-136.]
Cook’s distance:
An influence statistic designed to measure the shift in the estimated parameter vector, b, from fitting a regression model when a particular observation is omitted. It is a combined measure of the impact of that observation on all regression coefficients. The statistic is defined for the ith observation as
where r, is the standardized residual of the ith observation and h, is the ith diagonal element of the hat matrix, H arising from the regression analysis. Values of the statistic greater than one suggest that the corresponding observation has undue influence on the estimated regression coefficients. See also COVRATIO, DFBETA and DFFIT.
Fig. 45 An example of the convex hull of a set of bivariate data.
Cooperative study:
A term sometimes used for multicentre study.
Cophenetic correlation:
The correlation between the observed values in a similarity matrix or dissimilarity matrix and the corresponding fusion levels in the dendrogram obtained by applying an agglomerative hierarchical clustering method to the matrix. Used as a measure of how well the clustering matches the data.
Coplot:
A powerful visualization tool for studying how a response depends on an explanatory variable given the values of other explanatory variables. The plot consists of a number of panels one of which (the ‘given’ panel) shows the values of a particular explanatory variable divided into a number of intervals, while the others (the ‘dependence’ panels) show the scatterplots of the response variable and another explanatory variable corresponding to each interval in the given panel. The plot is examined by moving from left to right through the intervals in the given panel, while simultaneously moving from left to right and then from bottom to top through the dependence panels. The example shown (Fig. 46) involves the relationship between packed cell volume and white blood cell count for given haemoglobin concentration. [Visualizing Data, 1993, W.S. Cleveland, AT and T Bell Labs, New Jersey.]
Fig. 46 Coplot of haemoglobin concentration; reached cell volume and white blood cell count.
Copulas:
A class of bivariate probability distributions whose marginal distributions are uniform distributions on the uni t i nterval. An example is Frank’s family of bivariate distributions. Often used in frailty models for survival data. [KA1 Chapter 7.]
Cornfield, Jerome (1912-1979):
Cornfield studied at New York University where he graduated in history in 1933. Later he took a number of courses in statistics at the US Department of Agriculture. From 1935 to 1947 Cornfield was a statistician with the Bureau of Labour Statistics and then moved to the National Institutes of Health. In 1958 he was invited to succeed William Cochrane as Chairman of the Department of Biostatistics in the School of Hygiene and Public Health of the John Hopkins University. Cornfield devoted the major portion of his career to the development and application of statistical theory to the biomedical sciences, and was perhaps the most influential statistician in this area from the 1950s until his death. He was involved in many major issues, for example smoking and lung cancer, polio vaccines and risk factors for cardiovascular disease. Cornfield died on 17 September 1979 in Henden, Virginia.
Cornish, Edmund Alfred (1909-1973):
Cornish graduated in Agricultural Science at the University of Melbourne. After becoming interested in statistics he then completed three years of mathematical studies at the University of Adelaide and in 1937 spent a year at University College, London studying with Fisher. On returning to Australia he was eventually appointed Professor of Mathematical Statistics at the University of Adelaide in 1960. Cornish made important contributions to the analysis of complex designs with missing values and fiducial theory.
Correlated binary data:
Synonym for clustered binary data.
Correlated failure times:
Data that occur when failure times are recorded which are dependent. Such data can arise in many contexts, for example, in epidemiological cohort studies in which the ages of disease occurrence are recorded among members of a sample of families; in animal experiments where treatments are applied to samples of littermates and in clinical trials in which individuals are followed for the occurrence of multiple events. See also bivariate survival data. [Journal of the Royal Statistical Society, Series B, 2003, 65, 643-61.]
Correlated samples t-test:
Synonym for matched pairs t-test.
Correlation:
A general term for interdependence between pairs of variables. See also association.
Correlation coefficient:
An index that quantifies the linear relationship between a pair of variables. In a bivariate normal distribution, for example, the parameter, p. An estimator of p obtained from n sample values of the two variables of interest, (x1, y1), (x2, y2),…, (xn, yn), is Pearson’s product moment correlation coefficient, r, given by
The coefficient takes values between —1 and 1, with the sign indicating the direction of the relationship and the numerical magnitude its strength. Values of —1 or 1 indicate that the sample values fall on a straight line. A value of zero indicates the lack of any linear relationship between the two variables. See also Spearman’s rank correlation, intraclass correlation and Kendall’s tau statistics. [SMR Chapter 11.]
Correlation coefficient distribution:
The probability distribution, f (r), of Pearson’s product moment correlation coefficient when n pairs of observations are sampled from a bivariate normal distribution with correlation parameter, p. Given by
Correlation matrix:
A square, symmetric matrix with rows and columns corresponding to variables, in which the off-diagonal elements are correlations between pairs of variables, and elements on the main diagonal are unity. An example for measures of muscle and body fat is as follows:
Correlation matrix for muscle, skin and body fat data
| V1 | V2 | V3 | V4 | |
| V1 | (1.00 | 0.92 | 0.46 | 0.84 |
| R = V 2 | 0.92 | 1.00 | 0.08 | 0.88 |
| V 3 | 0.46 | 0.08 | 1.00 | 0.14 |
| V4 | V0.84 | 0.88 | 0.14 | 1.00 |
V1 = tricep(thickness mm), V2 = thigh(circumference mm), V3 = midarm(circumference mm), V4 = bodyfat(%).
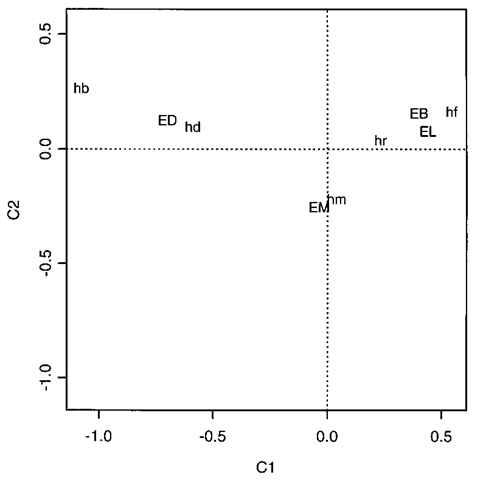
Correspondence analysis:
A method for displaying the relationships between categorical variables in a type of scatterplot diagram. For two such variables displayed in the form of a contingency table, for example, a set of coordinate values representing the row and column categories are derived. A small number of these derived coordinate values (usually two) are then used to allow the table to be displayed graphically. In the resulting diagram Euclidean distances approximate chi-squared distances between row and column categories. The coordinates are analogous to those resulting from a principal components analysis of continuous variables, except that they involve a partition of a chi-squared statistic rather than the total variance. Such an analysis of a contingency table allows a visual examination of any structure or pattern in the data, and often acts as a useful supplement to more formal inferential analyses. Figure 47 arises from applying the method to the following table.
Fig. 47 Correspondence analysis plot of hair colour/eye colour data.
| Eye Colour | Hair Colour | ||||
| Fair (hf) | Red (hr) | Medium (hm) | Dark (hd) | Black (hb) | |
| Light (EL) | 688 | 116 | 584 | 188 | 4 |
| Blue (EB) | 326 | 38 | 241 | 110 | 3 |
| Medium (EM) | 343 | 84 | 909 | 412 | 26 |
| Dark (ED) | 98 | 48 | 403 | 681 | 81 |
| [MV1 Chapter 5.] |
Cosine distribution:
Synonym for cardiord distribution.
Cosinor analysis:
The analysis of biological rhythm data, that is data with circadian variation, generally by fitting a single sinusoidal regression function having a known period of 24 hours, together with independent and identically distributed error terms.
Cost-benefit analysis:
A technique where health benefits are valued in monetary units to facilitate comparisons between different programmes of health care. The main practical problem with this approach is getting agreement in estimating money values for health outcomes.
Cost-effectiveness analysis:
A method used to evaluate the outcomes and costs of an intervention, for example, one being tested in a clinical trial. The aim is to allow decisions to be made between various competing treatments or courses of action. The results of such an analysis are generally summarized in a series of cost-effectiveness ratios.
Cost-effectiveness ratio (CER):
The ratio of the difference in cost between in test and standard health programme to the difference in benefit, respectively. Generally used as a summary statistic to compare competing health care programmes relative to their cost and benefit.
Cost of living extremely well index:
An index that tries to track the price fluctuations of items that are affordable only to those of very substantial means. The index is used to provide a barometer of economic forces at the top end of the market. The index includes 42 goods and services, including a kilogram of beluga malossal caviar and a face lift.
Count data:
Data obtained by counting the number of occurrences of particular events rather than by taking measurements on some scale.
Counter-matching:
An approach to selecting controls in nested case-control studies, in which a covariate is known on all cohort members, and controls are sampled to yield covariate-stratified case-control sets. This approach has been shown to be generally efficient relative to matched case-control designs for studying interaction in the case of a rare risk factor X and an uncorrelated risk factor Y.
Counting process:
A stochastic process {N(t), t > 0} in which N(t) represents the total number of ‘events’ that have occurred up to time t. The N(t) in such a process must satisfy;
Courant-Fisher minimax theorem:
This theorem states that for two quadratic forms, X’AX and X’BX, assuming that B is positive definite, then
where XL and XS are the largest and smallest relative eigenvalues respectively of A and B.
Covariance:
The expected value of the product of the deviations of two random variables, x and y, from their respective means, ax and ay, i.e.
The corresponding sample statistic is
where (xt, y,), i = 1,…, n are the sample values on the two variables and x and y their respective means. See also variance-covariance matrix and correlation coefficient.
Covariance inflation criterion:
A procedure for model selection in regression analysis.
Covariance structure models:
Synonym for structural equation models.
Covariates:
Often used simply as an alternative name for explanatory variables, but perhaps more specifically to refer to variables that are not of primary interest in an investigation, but are measured because it is believed that they are likely to affect the response variable and consequently need to be included in analyses and model building. See also analysis of covariance.
COVRATIO:
An influence statistic that measures the impact of an observation on the variance-covariance matrix of the estimated regression coefficients in a regression analysis. For the ith observation the statistic is given by
where s is the residual mean square from a regression analysis with all observations, X is the matrix appearing in the usual formulation of multiple regression and and X(_;) are the corresponding terms from a regression analysis with the ith observation omitted. Values outside the limits 1 ± 3(tr(H)/w) where H is the hat matrix can be considered extreme for purposes of identifying influential observations.
Cowles’ algorithm:
A hybrid Metropolis-Hastings, Gibbs sampling algorithm which overcomes problems associated with small candidate point probabilities.
Cox-Aalen model:
A model for survival data in which some covariates are believed to have multiplicative effects on the hazard function, whereas others have effects which are better described as additive. [Biometrics, 2003, 59, 1033-45.]
Cox and Plackett model:
A logistic regression model for the marginal probabilities from a 2×2 cross-over trial with a binary outcome measure.
Cox and Spj0tvoll method:
A method for partitioning treatment means in analysis of variance into a number of homogeneous groups consistent with the data.
Cox, Gertrude Mary (1900-1978):
Born in Dayton, Iowa, Gertrude Cox first intended to become a deaconess in the Methodist Episcopal Church. In 1925, however, she entered Iowa State College, Ames and took a first degree in mathematics in 1929, and the first MS degree in statistics to be awarded in Ames in 1931. Worked on psychological statistics at Berkeley for the next two years, before returning to Ames to join the newly formed Statistical Laboratory where she first met Fisher who was spending six weeks at the college as a visiting professor. In 1940 Gertrude Cox became Head of the Department of Experimental Statistics at North Carolina State College, Raleigh. After the war she became increasingly involved in the research problems of government agencies and industrial concerns. Joint authored the standard work on experimental design, Experimental Designs, with William Cochran in 1950. Gertrude Cox died on 17 October 1978.
Coxian-2 distribution:
The distribution of a random variable X such that
where X1 and X2 are independent random variables having exponential distributions with different means. [Scandinavian Journal of Statistics, 1996, 23, 419-41.]
Cox-Mantel test:
A distribution free method for comparing two survival curves. Assuming t(1) < t(2) < < l(K) to be the distinct survival times in the two groups, the test statistic is
where
In these formulae, r2 is the number of deaths in the second group, m^ the number of survival times equal to t(,), r^ the total number of individuals who died or were censored at time t(), and Aq is the proportion of these individuals in group two. If the survival experience of the two groups is the same then C has a standard normal distribution.
Cox-Snell residuals: Residuals widely used in the analysis of survival time data and defined as
where S^t,) is the estimated survival function of the ith individual at the observed survival time of t,-. If the correct model has been fitted then these residuals will be n observations from an exponential distribution with mean one.
Cox’s proportional hazards model:
A method that allows the hazard function to be modelled on a set of explanatory variables without making restrictive assumptions about the dependence of the hazard function on time. The model involved is
where x 1, X2, …, Xq are the explanatory variables of interest, and h(t) the hazard function. The so-called baseline hazard function, a(t), is an arbitrary function of time. For any two individuals at any point in time the ratio of the hazard functions is a constant. Because the baseline hazard function, a(t), does not have to be specified explicitly, the procedure is essentially a distribution free method. Estimates of the parameters in the model, i.e. fi1, …, fip, are usually obtained by maximum likelihood estimation, and depend only on the order in which events occur, not on the exact times of their occurrence. See also frailty and cumulative hazard function. [SMR Chapter 13.]
Cox’s test of randomness:
A test that a sequence of events is random in time against the alternative that there exists a trend in the rate of occurrence. The test statistic is
where n events occur at times t1, t2,…, tn during the time interval (0, T). Under the null hypothesis m has an Irwin-Hall distribution with mean 1 and variance As n increases the distribution of m under the null hypothesis approaches normality very rapidly and the normal approximation can be used safely for n > 20.
Craig’s theorem:
A theorem concerning the independence of quadratic forms in normal variables, which is given explicitly as:
For x having a multivariate normal distribution with mean vector k and variance-covariance matrix D, then x’Ax and x’Bx are stochastically independent if and only if ADB = 0. [American Statistician, 1995, 49, 59-62.] Cramer, Harald (1893-1985): Born in Stockholm, Sweden, Cramer studied chemistry and mathematics at Stockholm University. Later his interests turned to mathematics and he obtained a Ph.D. degree in 1917 with a thesis on Dirichlet series. In 1929 he was appointed to a newly created professorship in actuarial mathematics and mathematical statistics. During the next 20 years he made important contributions to central limit theorems, characteristic functions and to mathematical statistics in general. Cramer died 5 October 1985 in Stockholm.
Cramer-Rao lower bound:
A lower bound to the variance of an estimator of a parameter that arises from the Cramer-Rao inequality given by
Cramer-Rao lower bound:
A lower bound to the variance of an estimator of a parameter that arises from the Cramer-Rao inequality given by
where t is an unbiased estimator of some function of 0 say r(0), r is the derivative of r with respect to 0 and L is the relevant likelihood. In the case when r(0) = 0, then r’(0) = 1, so for an unbiased estimator of 0
where I is the value of Fisher’s information in the sample.
Cramer’s V:
A measure of association for the two variables forming a two-dimensional contingency table. Related to the phi-coefficient, 0, but applicable to tables larger than 2×2. The coefficient is given by
where r is the number of rows of the table and c is the number of columns. See also contingency coefficient, Sakoda coefficient and Tschuprov coefficient. [The Analysis of Contingency Tables, 2nd edition, 1993,Edward Arnold, London.]
Cramer-von Mises statistic:
A goodness-of-fit statistic for testing the hypothesis that the cumulative probability distribution of a random variable take some particular form, F0. If x1, x2,…, xn denote a random sample, then the statistic U is given by
where Fn(x) is the sample empirical cumulative distribution. [Journal of the American Statistical Association, 1974, 69, 730-7.]
Cramer-von M ises test:
A test of whether a set of observations arise from a normal distribution. The test statistic is
where the zt are found from the ordered sample values x(1) < X(2) < ••• < X(n) as
Critical values of W can be found in many sets of statistical tables.
Craps test:
A test for assessing the quality of random number generators.
Credible region:
Synonym for Bayesian confidence interval.
Credit scoring:
The process of determining how likely an applicant for credit is to default with repayments. Methods based on discriminant analysis are frequently employed to construct rules which can be helpful in deciding whether or not credit should be offered to an applicant.
Creedy and Martin generalized gamma distribution:
A probability distribution, f (x), given by
The normalizing constant ^ needs to be determined numerically. Includes many well-known distributions as special cases. For example, 01 = 03 = 04 = 0 corresponds to the exponential distribution and 03 = 04 = 0 to the gamma distribution. [Communication in Statistics - Theory and Methods, 1996, 25, 1825-36.]
Cressie-Read statistic:
A goodness-of-fit statistic which is, in some senses, somewhere between the chi-squared statistic and the likelihood ratio, and takes advantage of the desirable properties of both. [Journal of the Royal Statistical Society, Series B, 1979, 41, 54-64.]
Criss-cross design:
Synonym for strip-plot design.
Criteria of optimality:
Criteria for choosing between competing experimental designs. The most common such criteria are based on the eigenvalues A1,… ,Xp of the matrix X’X where X is the relevant design matrix. In terms of these eigenvalues three of the most useful criteria are:
A-optimality (A-optimal designs):
Minimize the sum of the variances of the parameter estimates
D-optimality(D-optimal designs): Minimize the generalized variance of the parameter estimates
E-optimality (E-optimal designs): Minimize the variance of the least well estimated contrast
All three criteria can be regarded as special cases of choosing designs to minimize
All three criteria can be regarded as special cases of choosing designs to minimize
For A-, D- and E-optimality the values of k are 1, 0 and 1, respectively.
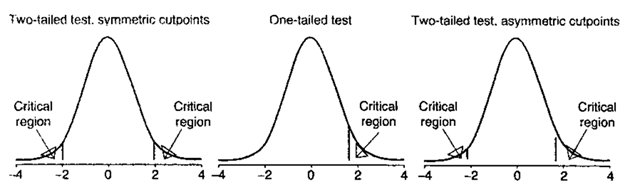
Critical region:
The values of a test statistic that lead to rejection of a null hypothesis. The size of the critical region is the probability of obtaining an outcome belonging to this region when the null hypothesis is true, i.e. the probability of a type I error. Some typical critical regions are shown in Fig. 48. See also acceptance region. [KA2 Chapter 21.]
Critical value:
The value with which a statistic calculated from sample data is compared in order to decide whether a null hypothesis should be rejected. The value is related to the particular significance level chosen. [KA2 Chapter 21.]
CRL:
Abbreviation for coefficient of racial likeness.
Cronbach’s alpha:
An index of the internal consistency of a psychological test. If the test consists of n items and an individual’s score is the total answered correctly, then the coefficient is given specifically by
where a is the variance of the total scores and a is the variance of the set of 0,1 scores representing correct and incorrect answers on item i. The theoretical range of the coefficient is 0 to 1. Suggested guidelines for interpretation are < 0.60 unacceptable, 0.60-0.65 undesirable, 0.65-0.70 minimally acceptable, 0.70-0.80 respectable, 0.80-0.90 very good, and > 0.90 consider shortening the scale by reducing the number of items.
Crossed treatments:
Two or more treatments that are used in sequence (as in a crossover design) or in combination (as in a factorial design).
Crossover design:
A type of longitudinal study in which subjects receive different treatments on different occasions. Random allocation is used to determine the order in which the treatments are received. The simplest such design involves two groups of subjects, one of which receives each of two treatments, A and B, in the order AB, while the other receives them in the reverse order. This is known as a two-by-two crossover design. Since the treatment comparison is ‘within-subject’ rather than ‘between-subject’, it is likely to require fewer subjects to achieve a given power. The analysis of such designs is not necessarily straightforward because of the possibility of carryover effects, that is residual effects of the treatment received on the first occasion that remain present into the second occasion. An attempt to minimize this problem is often made by including a wash-out period between the two treatment occasions. Some authorities have suggested that this type of design should only be used if such carryover effects can be ruled out a priori. Crossover designs are only applicable to chronic conditions for which short-term relief of symptoms is the goal rather than a cure. See also three-period crossover designs.
Fig. 48 Critical region.
Crossover rate:
The proportion of patients in a clinical trial transferring from the treatment decided by an initial random allocation to an alternative one.
Cross-sectional study:
A study not involving the passing of time. All information is collected at the same time and subjects are contacted only once. Many surveys are of this type. The temporal sequence of cause and effect cannot be addressed in such a study, but it may be suggestive of an association that should be investigated more fully by, for example, a prospective study.
Cross-validation:
The division of data into two approximately equal sized subsets, one of which is used to estimate the parameters in some model of interest, and the second is used to assess whether the model with these parameter values fits adequately. See also bootstrap and jackknife.
CRP:
Abbreviation for Chinese restaurant process.
Crude annual death rate:
The total deaths during a year divided by the total midyear population. To avoid many decimal places, it is customary to multiply death rates by 100000 and express the results as deaths per 100000 population. See also age-specific death rates and cause specific death rates.
Crude risk:
Synonym for incidence rate.
Cube law:
A law supposedly applicable to voting behaviour which has a history of several decades. It may be stated thus:
Consider a two-party system and suppose that the representatives of the two parties are elected according to a single member district system. Then the ratio of the number of representatives selected is approximately equal to the third power of the ratio of the national votes obtained by the two parties.
Cumulants:
A set of descriptive constants that, like moments, are useful for characterizing a probability distribution but have properties which are often more useful from a theoretical viewpoint. Formally the cumulants, k1,k2, …,icr are defined in terms of moments by the following identity in t:
Kr is the coefficient of (it)r/r\ in log 0{t) where 0{t) is the characteristic function of a random variable. The function f(t) = log 0{t) is known as the cumulant generating function. The relationships between the first three cumulants and first four central moments are as follows:
Cumulative distribution function:
A distribution showing how many values of a random variable are less than or more than given values. For grouped data the given values correspond to the class boundaries.
Cumulative frequency distribution:
The tabulation of a sample of observations in terms of numbers falling below particular values. The empirical equivalent of the cumulative probability distribution. An example of such a tabulation is shown below.
| Hormone assay values (nmol/l) | ||
| Class limits | i Cumulative frequency | |
| 75-79 | 1 | |
| 80-84 | 3 | |
| 85-89 | 8 | |
| 90-94 | 17 | |
| 95-99 | 27 | |
| 100-104 | 34 | |
| 105-109 | 38 | |
| 110-114 | 40 | |
| > 115 | 41 | |
Cumulative hazard function:
A function, H(t), used in the analysis of data involving survival times and given by
where h(t) is the hazard function. Can also be written in terms of the survival function, S(t), as H(t) = — ln S(t).
Cure rate models:
Models for survival times where there is a significant proportion of people who are cured. In general some type of finite mixture distribution is involved.
Curse of dimensionality:
A phrase first uttered by one of the witches in Macbeth. Now used to describe the exponential increase in number of possible locations in a multivariate space as dimensionality increases. Thus a single binary variable has two possible values, a 10-dimensional binary vector has over a thousand possible values and a 20-dimensional binary vector over a million possible values. This implies that sample sizes must increase exponentially with dimension in order to maintain a constant average sample size in the cells of the space. Another consequence is that, for a multivariate normal distribution, the vast bulk of the probability lies far from the centre if the dimensionality is large.
Curvature measures:
Diagnostic tools used to assess the closeness to linearity of a non-linear model. They measure the deviation of the so-called expectation surface from a plane with uniform grid. The expectation surface is the set of points in the space described by a prospective model, where each point is the expected value of the response variable based on a set of values for the parameters. [Applied Statistics, 1994, 43, 477-88.]
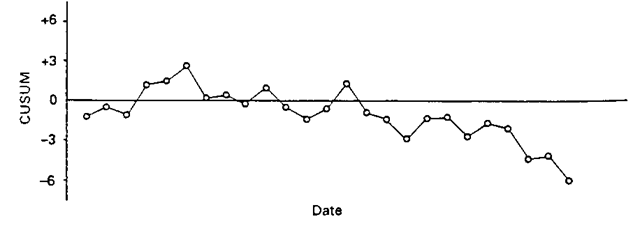
Cusum:
A procedure for investigating the influence of time even when it is not part of the design of a study. For a series X1, X2,…, Xn, the cusum series is defined as
where X0 is a reference level representing an initial or normal value for the data. Depending on the application, X0 may be chosen to be the mean of the series, the mean of the first few observations or some value justified by theory. If the true mean is X0 and there is no time trend then the cusum is basically flat. A change in level of the raw data over time appears as a change in the slope of the cusum. An example is shown in Fig. 49. See also exponentially weighted moving average control chart.
Cuthbert, Daniel (1905-1997):
Cuthbert attended MIT as an undergraduate, taking English and History along with engineering. He received a BS degree in chemical engineering in 1925 and an MS degree in the same subject in 1926. After a year in Berlin teaching Physics he returned to the US as an instructor at Cambridge School, Kendall Green, Maine. In the 1940s he read Fisher’s Statistical Methods for Research Workers and began a career in statistics. Cuthbert made substantial contributions to the planning of experiments particularly in an individual setting. In 1972 he was elected an Honorary Fellow of the Royal Statistical Society. Cuthbert died in New York City on 8 August 1997.
Cuzick’s trend test:
A distribution free method for testing the trend in a measured variable across a series of ordered groups. The test statistic is, for a sample of N subjects, given by
Fig. 49 Cusum chart.
where Z,(i = 1,…, N) is the group index for subject i (this may be one of the numbers 1,…, G arranged in some natural order, where G is the number of groups, or, for example, a measure of exposure for the group), and r, is the rank of the ith subject’s observation in the combined sample. Under the null hypothesis that there is no trend across groups, the mean and variance (<r2) of T are given by
where E(Z) and V(Z) are the calculated mean and variance of the Z values. [Statistics in Medicine, 1990, 9, 829-34.]
Cycle:
A term used when referring to time series for a periodic movement of the series. The period is the time it takes for one complete up-and-down and down-and-up movement.
Cycle hunt analysis:
A procedure for clustering variables in multivariate data, that forms clusters by performing one or other of the following three operations:
• combining two variables, neither of which belongs to any existing cluster,
• adding to an existing cluster a variable not previously in any cluster,
• combining two clusters to form a larger cluster.
Can be used as an alternative to factor analysis.
Cycle plot:
A graphical method for studying the behaviour of seasonal time series. In such a plot, the January values of the seasonal component are graphed for successive years, then the February values are graphed, and so forth. For each monthly subseries the mean of the values is represented by a horizontal line. The graph allows an assessment of the overall pattern of the seasonal change, as portrayed by the horizontal mean lines, as well as the behaviour of each monthly subseries. Since all of the latter are on the same graph it is readily seen whether the change in any subseries is large or small compared with that in the overall pattern of the seasonal component. Such a plot is shown in Fig. 50. [Visualizing Data, 1993, W.S. Cleveland, Hobart Press, Murray Hill, New Jersey.]
Cyclic designs:
Incomplete block designs consisting of a set of blocks obtained by cyclic development of an initial block. For example, suppose a design for seven treatments using three blocks is required, the (7) distinct blocks can be set out in a number of cyclic sets generated from different initial blocks, e.g. from (0,1,3)
Cyclic variation:
The systematic and repeatable variation of some variable over time. Most people’s blood pressure, for example, shows such variation over a 24 hour period, being lowest at night and highest during the morning. Such circadian variation is also seen in many hormone levels.
Fig. 50 Cycle plot of carbon dioxide concentrations.
Czekanowski coefficient:
A dissimilarity coefficient, dy, for two individuals i and j each having scores, xi = [xi1 ; Xi2; ... , Xiq ] and xj = [Xj1, Xj2,..., Xjq] on q variables, which is given by