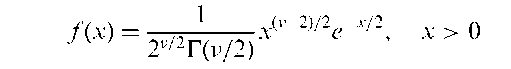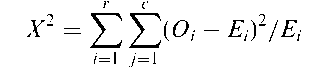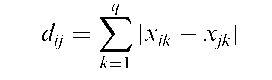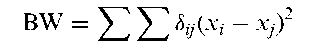C:
A low level programming language developed at Bell Laboratories. Widely used for software development.
C++:
A general purpose programming language which is a superset of C.
CACE:
Abbreviation for compiler average causal effect.
Calendar plot:
A method of describing compliance for individual patients in a clinical trial, where the number of tablets taken per day are set in a calendar-like-form – see Fig. 25. See also chronology plot. [Statistics in Medicine, 1997, 16, 1653-64.]
Calendarization:
A generic term for benchmarking.
Calibration:
A process that enables a series of easily obtainable but inaccurate measurements of some quantity of interest to be used to provide more precise estimates of the required values. Suppose, for example, there is a well-established, accurate method of measuring the concentration of a given chemical compound, but that it is too expensive and/or cumbersome for routine use. A cheap and easy to apply alternative is developed that is, however, known to be imprecise and possibly subject to bias. By using both methods over a range of concentrations of the compound, and applying regression analysis to the values from the cheap method and the corresponding values from the accurate method, a calibration curve can be constructed that may, in future applications, be used to read off estimates of the required concentration from the values given by the less involved, inaccurate method. [KA2 Chapter 28.]
Campion, Sir Harry (1905-1996):
Born in Worsley, Lancashire, Campion studied at Manchester University where, in 1933, he became Robert Ottley Reader in Statistics. In the Second World War he became Head of the newly created
| Mon | Tue | Wed | Thr | Fri | Sat | Sun | |
| 0 | 1 | ||||||
| 3 | 1 | 1 | 2 | 1 | 0 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 17 | 0 | 1 | 1 | 2 | 0 | 2 | 0 |
| 24 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 31 | 1 |
Fig. 25 Calendar plot of number of tablets taken per day.
Central Statistical Office remaining in this position until his retirement in 1967. Campion was responsible for drafting the Statistics of Trade Act 1947 and in establishing a new group in the civil service—the Statistician class. He was President of the Royal Statistical Society from 1957 to 1959 and President of the International Statistical Institute from 1963 to 1967. Awarded the CBE in 1945 and a knighthood in 1957.
Canberra metric:
A dissimilarity coefficient given by
where xik, Xjk, k = 1,…, q are the observations on q variables for individuals i and j.
CAN estimator:
An estimator of a parameter that is consistent and asymptotically normal.
Canonical correlation analysis:
A method of analysis for investigating the relationship between two groups of variables, by finding linear functions of one of the sets of variables that maximally correlate with linear functions of the variables in the other set. In many respects the method can be viewed as an extension of multiple regression to situations involving more than a single response variable. Alternatively it can be considered as analogous to principal components analysis except that a correlation rather than a variance is maximized. A simple example of where this type of technique might be of interest is when the results of tests for, say, reading speed (x1), reading power (x2), arithmetical speed (y1), and arithmetical power (y4), are available from a sample of school children, and the question of interest is whether or not reading ability (measured by x1 and x2) is related to arithmetical ability (as measured by y1 and y2).
Capture-recapture sampling:
An alternative approach to a census for estimating population size, which operates by sampling the population several times, identifying individuals which appear more than once. First used by Laplace to estimate the population of France, this approach received its main impetus in the context of estimating the size of wildlife populations. An initial sample is obtained and the individuals in that sample marked or otherwise identified. A second sample is, subsequently, independently obtained, and it is noted how many individuals in that sample are marked. If the second sample is representative of the population as a whole, then the sample proportion of marked individuals should be about the same as the corresponding population proportion. From this relationship the total number of individuals in the population can be estimated. Specifically if X individuals are ‘captured’, marked and released and y individuals then independently captured of which x are marked, then the estimator of population size (sometimes known as the Petersen estimator) is
with variance given by
The estimator does not have finite expectation since x can take the value zero. A modified version, Chapman’s estimator, adds one to the frequency of animals caught in both samples (x) with the resulting population size estimator
Cardiord distribution:
A probability distribution, f (0), for a circular random variable, 0, given by
CART:
Abbreviation for classification and regression tree technique.
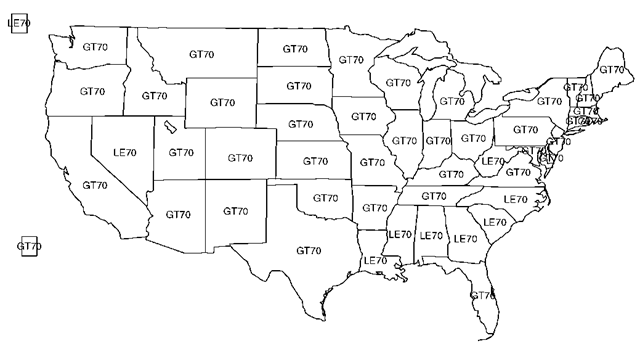
Cartogram:
A diagram in which descriptive statistical information is displayed on a geographical map by means of shading or by using a variety of different symbols. An example is given at Fig. 26. See also disease mapping. [Statistics in Medicine, 1988, 7, 491-506.]
Case-cohort study:
A study that involves sampling from a cohort of interest and using that sample as a comparison group for all cases that occur in the cohort. The design is generally used when the cohort can be followed for disease outcome, but it is too expensive to collect and process information on all study subjects.
Fig. 26 Cartogram of life expectancy in the USA, by state: LE70 = 70 years or less, GT70 = more than 70 years.
Catastrophe theory:
A theory of how small, continuous changes in independent variables can have sudden, discontinuous effects on dependent variables. Examples include the sudden collapse of a bridge under slowly mounting pressure, and the freezing of water when temperature is gradually decreased. Developed and popularized in the 1970s, catastrophe theory has, after a period of criticism, now become well established in physics, chemistry and biology.
Categorical variable:
A variable that gives the appropriate label of an observation after allocation to one of several possible categories, for example, marital status: married, single or divorced, or blood group: A, B, AB or O. The categories are often given numerical labels but for this type of data these have no numerical significance. See also binary variable, continuous variable and ordinal variable.
Categorizing continous variables:
A practice that involves the conversion of continuous variables into a series of categories, that is common in medical research. The rationale is partly statistical (avoidance of certain assumptions about the nature of the data) and partly that clinicians are often happier when categorizing individuals. In general there are no statistical advantages in such a procedure.
Cauchy, Augustin-Louis (1789-1857):
Born in Paris, Cauchy studied to become an Engineer but ill health forced him to retire and teach mathematics at the Ecole Polytechnique. Founder of the theory of functions of a complex variable, Cauchy also made considerable contributions to the theory of estimation and the classical linear model. He died on 22 May 1857 in Sceaux, France.
Cauchy distribution:
The probability distribution, f (x), given by
where a is a location parameter (median) and f a scale parameter. Moments and cumulants of the distribution do not exist. The distribution is unimodal and symmetric about a with much heavier tails than the normal distribution (see Fig. 27). The upper and lower quartiles of the distribution are a ± f. Named after Augustin-Louis Cauchy (1789-1857). [STD Chapter 7.]
Cauchy integral:
The integral of a function,f (x), from a to b defined in terms of the sum
where the range of the integral (a, b) is divided at points x1, x2,…, xn. It may be shown that under certain conditions (such as the continuity of f(x) in the range) the sum tends to a limit as the length of the intervals tends to zero, independently of where the dividing points are drawn or the way in which the tendency to zero proceeds. This limit is the required integral. See also Riemann-Steltjes integral. [KA1 Chapter 1.]
Cauchy-Schwarz inequality:
The following inequality for the integrals of functions, f (x), and g(x), whose squares are integral
In statistics this leads to the following inequality for expected values of two random variables x and y with finite second moments
Fig. 27 Cauchy distributions for various parameter values.
The result can be used to show that the correlation coefficient, p, satisfies the inequality p2 < 1.
Causality:
The relating of causes to the effects they produce. Many investigations in medicine seek to establish causal links between events, for example, that receiving treatment A causes patients to live longer than taking treatment B. In general the strongest claims to have established causality come from data collected in experimental studies. Relationships established in observational studies may be very suggestive of a causal link but are always open to alternative explanations.
Cause specific death rate:
A death rate calculated for people dying from a particular disease. For example, the following are the rates per 1000 people for three disease classes for developed and developing countries in 1985.
| C1 | C2 | C3 |
| Developed 0.5 | 4.5 | 2.0 |
| Developing 4.5 | 1.5 | 0.6 |
| C1 = Infectious and parasitic diseases | ||
| C2 = Circulatory diseases | ||
| C3 = Cancer |
Ceiling effect:
A term used to describe what happens when many subjects in a study have scores on a variable that are at or near the possible upper limit (‘ceiling’). Such an effect may cause problems for some types of analysis because it reduces the possible amount of variation in the variable. The converse, or floor effect, causes similar problems. [Arthritis and Rheumatism, 1995, 38, 1055.]
Cellular proliferation models:
Models used to describe the growth of cell populations. One example is the deterministic model
where N(t) is the number of cells in the population at time t, t0 is an initial time and v represents the difference between a constant birth rate and a constant death rate. Often also viewed as a stochastic process in which N(t) is considered to be a random variable. [Investigative Ophthalmology and Visual Science, 1986, 27, 1085-94.]
Censored data plots:
Graphical methods of portraying censored data in which grey scale or colour is used to encode the censoring information in a two-dimensional plot. An example arising from a randomized clinical trial on liver disease is shown in Fig. 28.
Censored observations:
An observation xt on some variable of interest is said to be censored if it is known only that x{ < L{ (left-censored) or x{ > U (right-censored) where Lt and U are fixed values. Such observations arise most frequently in studies where the main response variable is time until a particular event occurs (for example, time to death) when at the completion of the study, the event of interest has not happened to a number of subjects. See also interval censored data, singly censored data, doubly censored data and non-informative censoring.
Censored regression models:
A general class of models for analysing truncated and censored data where the range of the dependent variable is constrained. A typical case of censoring occurs when the dependent variable has a number of its values concentrated at a limiting value, say zero.
Fig. 28 Censored data plot of data from a randomized clinical trial on liver disease: censored individuals are plotted as octagons: uncensored individuals are plotted in grey scale.
Census:
A study that aims to observe every member of a population. The fundamental purpose of the population census is to provide the facts essential to government policy-making, planning and administration.
Centile:
Synonym for percentile.
Centile reference charts:
Charts used in medicine to observe clinical measurements on individual patients in the context of population values. If the population centile corresponding to the subject’s value is atypical (i.e. far from the 50% value) this may indicate an underlying pathological condition. The chart can also provide a background with which to compare the measurement as it changes over time. An example is given in Fig. 29. [Statistics in Medicine, 1996, 15, 2657-68.]
Centralized database:
A database held and maintained in a central location, particularly in a multicentre study.
Fig. 29 Centile chart of birthweight for gestational age.
Central limit theorem:
If a random variable Y has population mean ^ and population variance a2, then the sample mean, y, based on n observations, has an approximate normal distribution with mean and variance a2 =n, for sufficiently large n. The theorem occupies an important place in statistical theory. [KA1 Chapter 8.]
Central range:
The range within which the central 90% of values of a set of observations lie. [SMR Chapter 3.]
Central tendency:
A property of the distribution of a variable usually measured by statistics such as the mean, median and mode.
Centroid method:
A method of factor analysis widely used before the advent of high-speed computers but now only of historical interest.
CEP:
Abbreviation for circular error probable.
CER:
Abbreviation for cost-effectiveness ratio.
CERES plot:
Abbreviation for combining conditional expectations and residuals plot.
CFA:
Abbreviation for confirmatory factor analysis.
CHAID:
Abbreviation for chi-squared automated interaction detector.
Chain-binomial models:
Models arising in the mathematical theory of infectious diseases, that postulate that at any stage in an epidemic there are a certain number of infected and susceptibles, and that it is reasonable to suppose that the latter will yield a fresh crop of cases at the next stage, the number of new cases having a binomial distribution. This results in a ‘chain’ of binomial distributions, the actual probability of a new infection at any stage depending on the numbers of infectives and susceptibles at the previous stage.
Chaining:
A phenomenon often encountered in the application of single linkage clustering which relates to the tendency of the method to incorporate intermediate points between distinct clusters into an existing cluster rather than initiate a new one.
Chain-of-events data:
Data on a succession of events that can only occur in a prescribed order. One goal in the analysis of this type of data is to determine the distribution of times between successive events.
Chains of infection:
A description of the course of an infection among a set of individuals.
The susceptibles infected by direct contact with the introductory cases are said to make up the first generation of cases; the susceptibles infected by direct contact with the first generation are said to make up the second generation and so on. The enumeration of the number of cases in each generation is called an epidemic chain. Thus the sequence 1-2-1-0 denotes a chain consisting of one introductory case, two first generation cases, one second generation case and no cases in later generations.
Chalmers, Thomas Clark (1917-1995):
Born in Forest Hills, New York, Chalmers graduated from Columbia University College of Physicians and Surgeons in 1943. After entering private practice he became concerned over the lack of knowledge on the efficacy of accepted medical therapies, and eventually became a leading advocate for clinical trials, and later for meta-analysis setting up a meta-analysis consultancy company at the age of 75. In a distinguished research and teaching career, Chalmers was President and Dean of the Mount Sinai Medical Center and School of Medicine in New York City from 1973 to 1983. He died on 27 December 1995, in Hanover, New Hampshire.
Champernowne, David Gawen (1912-2000):
Born in Oxford, Champernowne studied mathematics at King’s College, Cambridge, later switching to economics, and gaining first class honours in both. Before World War II he worked at the London School of Economics and then at Cambridge where he demonstrated that the evolution of an income and wealth distribution could be represented by a Markovian model of income mobility. During the war he worked at the Ministry of Aircraft Production, and at the end of the war became Director of the Oxford Institute of Statistics. In 1948 he was made Professor of Statistics at Oxford, and carried out work on the application of Bayesian analysis to autoregressive series. In 1958 Champernowne moved to Cambridge and continued research into the theory of capital and the measurement of economic inequality. He died on 22 August 2000.
Change point problems:
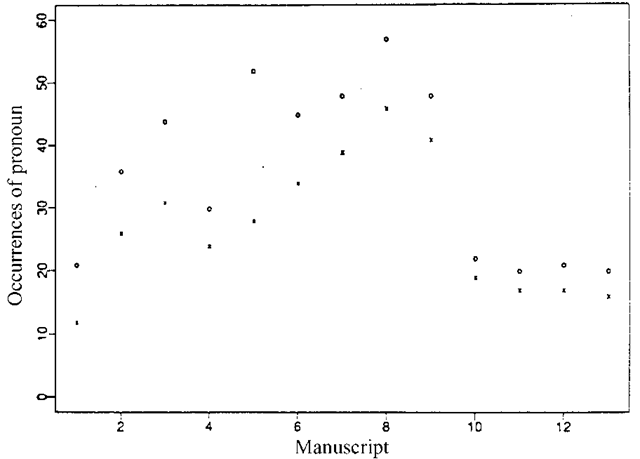
Problems with chronologically ordered data collected over a period of time during which there is known (or suspected) to have been a change in the underlying data generation process. Interest then lies in, retrospectively, making inferences about the time or position in the sequence that the change occurred. A famous example is the Lindisfarne scribes data in which a count is made of the occurrences of a particular type of pronoun ending observed in 13 chronologically ordered medieval manuscripts believed to be the work of more than one author. A plot of the data (see Fig. 30) shows strong evidence of a change point. A simple example of a possible model for such a problem is the following;
Fig. 30 A plot of the Lindisfarne scribes data indicating a clear change point.
Interest would centre on estimating the parameters in the model particularly the change point, r.
Change scores:
Scores obtained by subtracting a post-treatment score on some variable from the corresponding pre-treatment, baseline value. Often used as the basis for analysis of longitudinal studies despite being known to be less effective than using baseline measures as covariates. When used to compare groups formed on the basis of extreme values of some variable and then observed before and after a treatment, such scores may be affected by the phenomenon of regression to the mean. See also adjusting for baseline and baseline balance. [SMR Chapter 14.]
Chaos:
Apparently random behaviour exhibited by a deterministic model.
Characteristic function:
A function, 0(t), derived from a probability distribution, f (x), as
where i = — 1 and t is real. The function is of great theoretical importance and under certain general conditions determines and is completely determined by the probability distribution. If <f>(t) is expanded in powers of t then the rth central moment, fj,’r, is equal to the coefficient of (it)r/r! in the expansion. Thus the characteristic function is also a moment generating function.
Characteristic root:
Synonym for eigenvalue.
Characteristic vector:
Synonym for eigenvector.
Chebyshev-Hermite polynomial:
A function, Hr(x) defined by the identity
The polynomials have an important orthogonal property namely that
Used in the Gram-Charlier Type A series.
Chebyshev, Pafnuty Lvovich (1821-1894):
Born in Okatovo, Russia, Chebyshev studied at Moscow University. He became professor at St Petersburg in 1860, where he founded the Petersburg mathematical school which influenced Russian mathematics for the rest of the century. Made important contributions to the theory of the distribution of prime numbers, but most remembered for his work in probability theory where he proved a number of fundamental limit theorems. Chebyshev died on 8 December 1894 in St Petersburg, Russia.
Chebyshev’s inequality:
A statement about the proportion of observations that fall within some number of standard deviations of the mean for any probability distribution. One version is that for a random variable, X
where k is the number of standard deviations, a, from the mean, For example, the inequality states that at least 75% of the observations fall within two standard deviations of the mean. If the variable X can take on only positive values then the following, known as the Markov inequality, holds;
Chemometrics:
The application of mathematical and statistical methods to problems in Chemistry.
Chernoff’s faces:
A technique for representing multivariate data graphically. Each observation is represented by a computer-generated face, the features of which are controlled by an observation’s variable values. The collection of faces representing the set of observations may be useful in identifying groups of similar individuals, outliers, etc. See Fig. 31. See also Andrews’ plots and glyphs.
Chi-bar squared distribution:
A term used for a mixture of chi-squared distributions that is used in the simultaneous modelling of the marginal distributions and the associati on between two categorical variables.
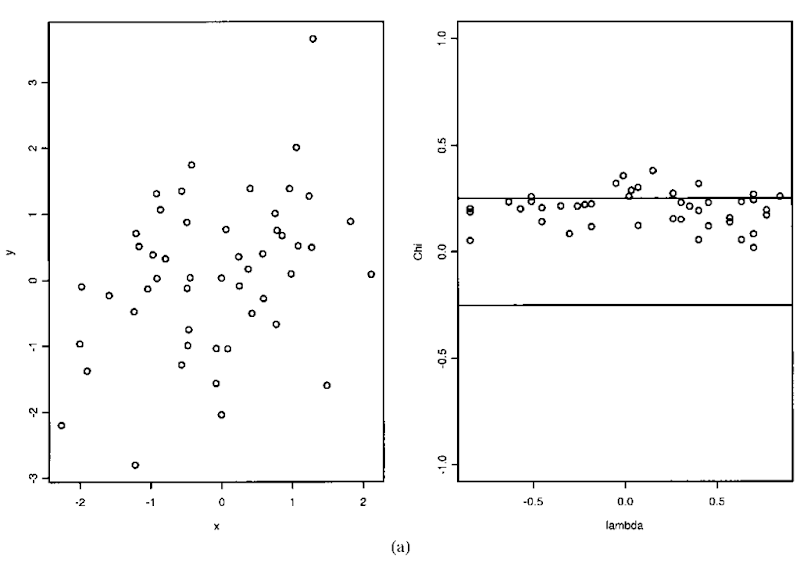
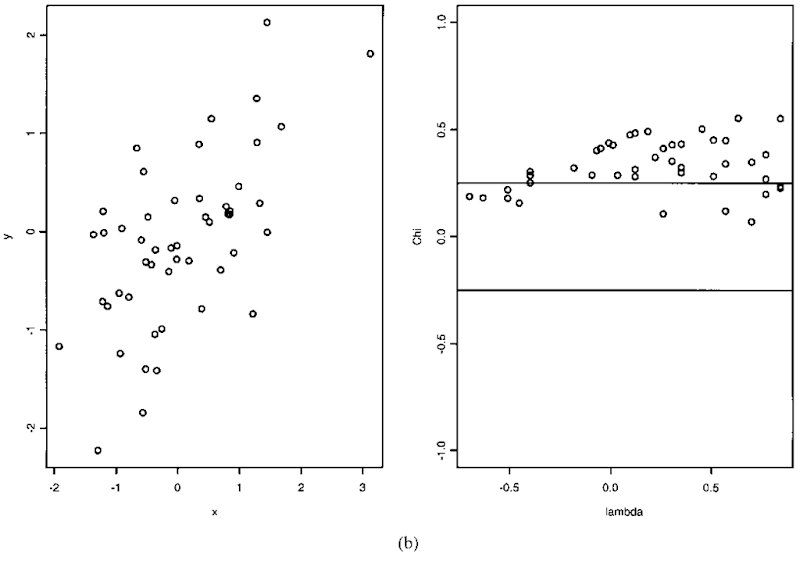
Chi-plot:
An auxiliary display to the scatterplot in which independence is manifested in a characteristic way. The plot provides a graph which has characteristic patterns depending on whether the variates are (1) independent, (2) have some degree of monotone relationship, (3) have more complex dependence structure. The plot depends on the data only through the values of their ranks. The plot is a scatterplot
with (x1, y1) … (xn, yn) being the observed sample values, and I(A) being the indicator function of the event A. Example plots are shown in Figure 32. Part (a) shows the situation in which x and y are independent, Part (b) in which they have a correlation of 0.6. In each case the left hand plot is a simple scatterplot of the data, and the right hand is the corresponding chi-plot.
Fig. 31 Chernoffs faces representing ten multivariate observations.
Chi-squared automated interaction detector (CHAID):
Essentially an automaticinter-action detector for binary target variables.
Chi-squared distance:
A distance measure for categorical variables that is central to correspondence analysis. Similar to Euclidean distance but effectively compensates for the different levels of occurrence of the categories.
Chi-squared distribution:
The probability distribution, f (x), of a random variable defined as the sum of squares of a number (v) of independent standard normal variables and given by
The shape parameter, v, is usually known as the degrees of freedom of the distribution. This distribution arises in many areas of statistics, for example, assessing the goodness-of-fit of models, particularly those fitted to contingency tables. The mean of the distribution is v and its variance is 2v.
Fig. 32 Chi-plot. (a) Uncorrelated situation. (b) Correlated situation.
Chi-squared probability plot:
A procedure for testing whether a set of multivariate data have a multivariate normal distribution. The ordered generalized distances
where xi, i = 1,…, n, are multivariate observations involving q variables, X is the sample mean vector and S the sample variance-covariance matrix, are plotted against the quantiles of a chi-squared distribution with q degrees of freedom. Deviations from multivariate normality are indicated by depatures from a straight line in the plot. An example of such a plot appears in Fig. 33. See also quantile-quantile plot. [Principles of Multivariate Analysis, 2nd edition, 2000, W.J. Krzanowski, Oxford Science Publications, Oxford.]
Chi-squared statistic:
A statistic having, at least approximately, a chi-squared distribution.
An example is the test statistic used to assess the independence of the two variables forming a contingency table
where Oi represents an observed frequency and Ei the expected frequency under independence. Under the hypothesis of independence X has, approximately, a chi-squared distribution with (r — 1)(c — 1) degrees of freedom.
Chi-squared test for trend:
A test applied to a two-dimensional contingency table in which one variable has two categories and the other has k ordered categories, to assess whether there is a difference in the trend of the proportions in the two groups. The result of using the ordering in this way is a test that is more powerful than using the chi-squared statistic to test for independence.
Chinese restaurant process (CRP):
A distribution on partitions of the integers obtained by imagining a process by which M customers sit down in a Chinese restaurant with an infinite number of tables. (The terminology was inspired by the Chinese restaurants in San Francisco which seem to have an infinite seating capacity.) The basic process is specified as follows. The first customer sits at the first table, and the mth customer sits at a table drawn from the following distribution:
where mi is the number of previous customers at table i and y is a parameter. After M customers sit down, the seating plan gives a partition of M items. The CRP has been used to represent uncertainty over the number of components in a finite mixture distribution.
Fig. 33 Chi-squared probability plot indicating data do not have a multivariate normal distribution.
Choleski decomposition:
The decomposition of a symmetric matrix, A (which is not a singular matrix), into the form
A = LL0
where L is a lower triangular matrix. Widely used for solving linear equations and matrix inversion.
Chow test:
A test of the equality of two independent sets of regression coefficients under the assumption of normally distributed errors.
Christmas tree boundaries:
An adjustment to the stopping rule in a sequential clinical trial for the gaps between the ‘looks’.
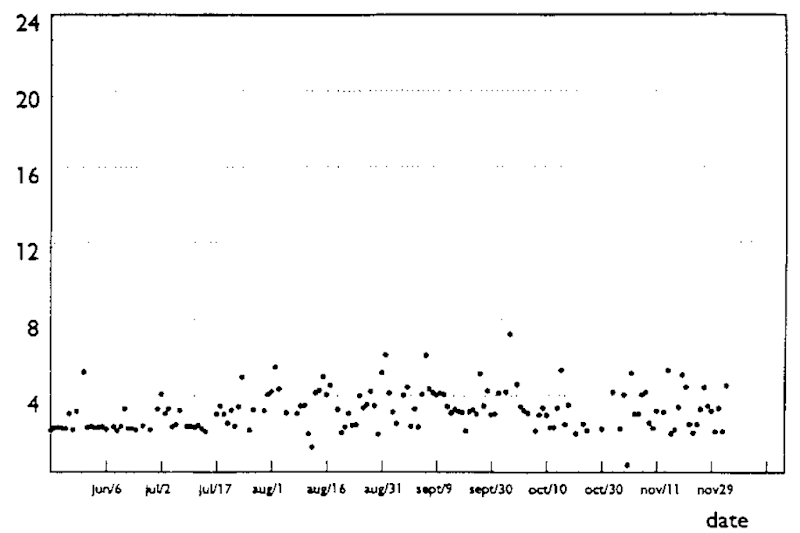
Chronology plot:
A method of describing compliance for individual patients in a clinical trial, where the times that a tablet are taken are depicted over the study period (see Fig. 34). See also calendar plot.
Fig. 34 Chronology plot of times that a tablet is taken in a clinical trial.
Chronomedicine:
The study of the mechanisms underlying variability in circadian and other rhythms found in human beings.
The variation that takes place in variables such as blood pressure and body temperature over a 24 hour period. Most living organisms experience such variation which corresponds to the day/night cycle caused by the Earth’s rotation about its own axis.
Circular data:
Observations on a circular random variable.
Circular distribution:
A probability distribution, f (6), of a circular random variable, 6 which ranges from 0 to 2n so that the probability may be regarded as distributed around the circumference of a circle. The function f is periodic with period 2n so that f(6 + 2^) =f(6). An example is the von Mises distribution. See also cardiord distribution. [KA1 Chapter 5.]
Circular error probable:
An important measure of accuracy for problems of directing projectiles at targets, which is the bivariate version of a 50% quantile point. Defined explicitly as the value R such that on average half of a group of projectiles will fall within the circle of radius R about the target point.
Circular random variable:
An angular measure confined to be on the unit circle. Figure 35 shows a representation of such a variable. See also cardiord distribution and von Mises distribution.
City-block distance:
A distance measure occasionally used in cluster analysis and given by
Fig. 35 Diagram illustrating a circular random variable.
where q is the number of variables and xik, xjk, k = 1,…, q are the observations on individuals i and j. [MV2 Chapter 10.]
Class frequency:
The number of observations in a class interval of the observed frequency distribution of a variable.
Classical scaling:
A form of multidimensional scaling in which the required coordinate values are found from the eigenvectors of a matrix of inner products.
Classical statistics:
Synonym for frequentist inference.
Classification and regression tree technique (CART):
An alternative to multiple regression and associated techniques for determining subsets of explanatory variables most important for the prediction of the response variable. Rather than fitting a model to the sample data, a tree structure is generated by dividing the sample recursively into a number of groups, each division being chosen so as to maximize some measure of the difference in the response variable in the resulting two groups. The resulting structure often provides easier interpretation than a regression equation, as those variables most important for prediction can be quickly identified. Additionally this approach does not require distributional assumptions and is also more resistant to the effects of outliers. At each stage the sample is split on the basis of a variable, xi, according to the answers to such questions as ‘Is xi < c’ (univariate split), is ‘J2 aixi < c’ (linear function split) and ‘does xi 2 A’ (if xi is a categorical variable). An illustration of an application of this method is shown in Fig. 36. See also automatic interaction detector.
Classification matrix:
A term often used in discriminant analysis for the matrix summarizing the results obtained from the derived classification rule, and obtained by crosstabu-lating observed against predicted group membership. Contains counts of correct classifications on the main diagonal and incorrect classifications elsewhere.
Fig. 36 An example of a CART diagram showing classification of training cases in a credit risk assessment exercise.
Classification techniques:
A generic term used for both cluster analysis methods and discriminant methods although more widely applied to the former.
Class intervals:
The intervals of the frequency distribution of a set of observations.
Clemmesen’s hook:
A phenomenon sometimes observed when interpreting parameter estimates from age-period-cohort models, where rates increase to some maximum, but then fall back slightly before continuing their upward trend.
Cliff and Ord’s BW statistic:
A measure of the degree to which the presence of some factor in an area (or time period) increases the chances that this factor will be found in a nearby area. Defined explicitly as
where xi = 1 if the ith area has the characteristic and zero otherwise and Sj = 1 if areas i and j are adjacent and zero otherwise. See also adjacency matrix and Moran’s I.
Clinical epidemiology:
The application of epidemiological methods to the study of clinical phenomena, particularly diagnosis, treatment decisions and outcomes.
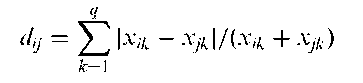
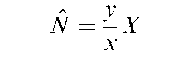
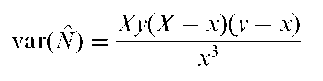
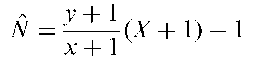
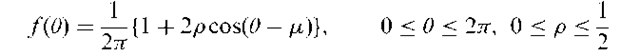
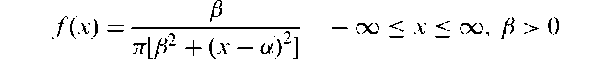
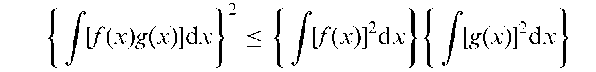
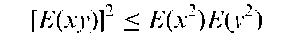



![tmpCD-140_thumb[1] tmpCD-140_thumb[1]](http://lh3.ggpht.com/_1wtadqGaaPs/THZgdxQxSgI/AAAAAAAAU7g/_LcIuZNmKIE/tmpCD140_thumb1_thumb.png?imgmax=800)
![tmpCD-142_thumb[2] tmpCD-142_thumb[2]](http://lh5.ggpht.com/_1wtadqGaaPs/THZgiJDmDRI/AAAAAAAAU7w/H9YRzOsO-sM/tmpCD142_thumb2_thumb.png?imgmax=800)
![tmpCD-143_thumb[1] tmpCD-143_thumb[1]](http://lh5.ggpht.com/_1wtadqGaaPs/THZglY11cwI/AAAAAAAAU74/fx-q4PFjClk/tmpCD143_thumb1_thumb.png?imgmax=800)
![tmpCD-144_thumb[2] tmpCD-144_thumb[2]](http://lh3.ggpht.com/_1wtadqGaaPs/THZgneRfPAI/AAAAAAAAU8A/w7BlcKICYJ8/tmpCD144_thumb2_thumb.png?imgmax=800)
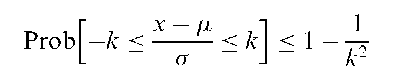
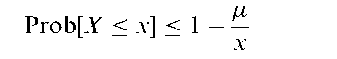
![tmpCD-147_thumb[2] tmpCD-147_thumb[2]](http://lh5.ggpht.com/_1wtadqGaaPs/THZhBLKumvI/AAAAAAAAU8Y/Jt6TlrCzl_E/tmpCD147_thumb2_thumb.png?imgmax=800)