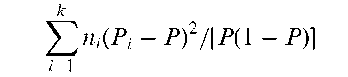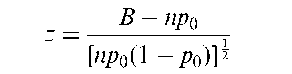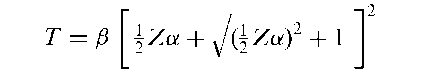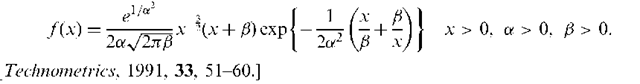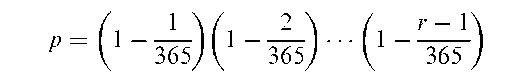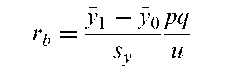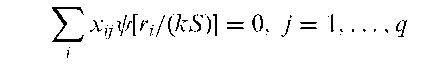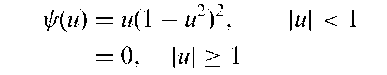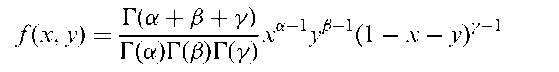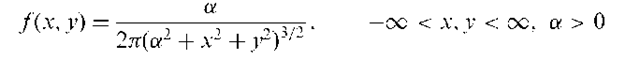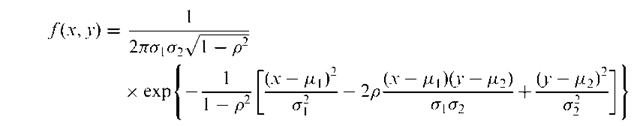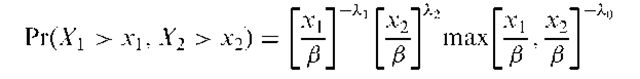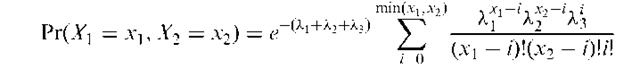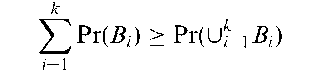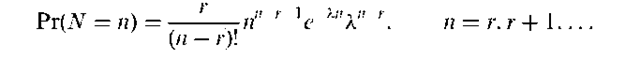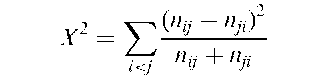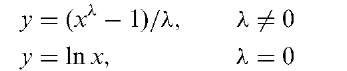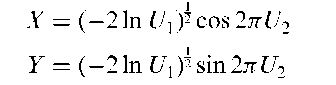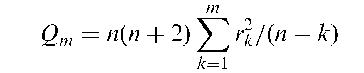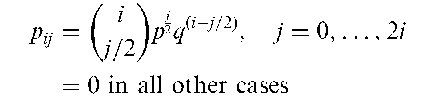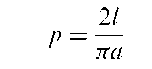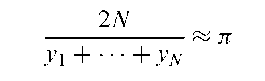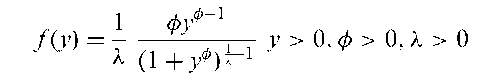Binomial failure rate model:
A model used to describe the underlying failure process in a system whose components can be subjected to external events (‘shocks’) that can cause the failure of two or more system components. For a system of m indentical components, the model is based on m +1 independent Poisson processes, {NS (t), t > 0}, {Ni(t), t > 0}, i = 1;…, m. The quantities Ni determine individual component failures and have equal intensity rate X. The variables NS are system shocks with rate that represent the external events affecting all components within the system. Given the occurrence of a system shock, each component fails with probability p, independently of the other components, hence the number of failures due to the system shock has a binomial distribution with parameters (m, p).
Binomial index of dispersion:
An index used to test whether k samples come from populations having binomial distributions with the same parameter p. Specifically the index is calculated as
where n1, n2,…, nk are the respective sample sizes, P1, P2,…, Pk are the separate sample estimates of the probability of a ‘success’, and P is the mean proportion of successes taken over all samples. If the samples are all from a binomial distribution with parameter p, the index has a chi-squared distribution with k — 1 degrees of freedom. See also index of dispersion. [Biometrika, 1966, 53, 167-82.] Binomial test: A procedure for making inferences about the probability of a success p, in a series of independent repeated Bernoulli trials. The test statistic is the observed number of successes, B. For small sample sizes critical values for B can be obtained from appropriate tables. A large-sample approximation is also available based on the asymptotic normality of B. The test statistic in this case is
where p0 is the hypothesised value of p. When the hypothesis is true z has an asymptotic standard normal distribution. See also Clopper-Pearson interval.
Bioassay:
An abbreviation of biological assay, which in its classical form involves an experiment conducted on biological material to determine the relative potency of test and standard preparations. Recently however, the term has been used in a more general sense, to denote any experiment in which responses to various doses of externally applied agents are observed in animals or some other biological system. See also calibration and probit analysis.
Bioavailability:
The rate and extent to which an active ingredient of a drug product is absorbed and becomes available at the site of drug action.
Bioavailability study:
A study designed to assess the pharmacological characteristics of a new drug product during Phase I clinical development or to compare the bioavail-ability of different formulations of the same drug (for example, tablets versus capsules).
Bioequivalence:
The degree to which clinically important outcomes of treatment by a new preparation resemble those of a previously established preparation.
Bioequivalence trials:
Clinical trials carried out to compare two or more formulations of a drug containing the same active ingredient, in order to determine whether the different formulations give rise to comparable blood levels.
Bioinformatics:
Essentially the application of information theory to biology to deal with the deluge of information resulting from advances in molecular biology. The main tasks in this field are the creation and maintenance of databases of biological information, particularly nucleic acid sequences, finding the genes in the DNA sequences of various organisms and clustering protein sequences into families of related sequences.
(Bio)sequence analysis:
The statistical analysis of nucleotide sequence data of deoxyribonucleic acid (DNA) or amino acid sequence data of polypeptides, with the purpose of predicting structure or function, or identifying similar sequences that may represent homology (i.e. share comon evolutionary origin).
Biostatistics:
A narrow definition is ‘the branch of science which applies statistical methods to biological problems’. More commonly, however, it also includes statistics applied to medicine and health sciences.
Biplots:
The multivariate analogue of scatterplots, which approximate the multivariate distribution of a sample in a few dimensions, typically two, and superimpose on this display representations of the variables on which the samples are measured. The relationships between the individual sample points can be easily seen and they can also be related to the values of the measurements, thus making such plots useful for providing a graphical description of the data, for detecting patterns, and for displaying results found by more formal methods of analysis. Figure 16 shows the two-dimensional biplot of a set of multivariate data with 34 observations and 10 variables.
Bipolar factor:
A factor resulting from the application of factor analysis which has a mixture of positive and negative loadings. Such factors can be difficult to interpret and attempts are often made to simplify them by the process of factor rotation.
BIRMD:
Abbreviation for balanced incomplete repeated measures design.
Birnbaum, Allan (1923-1976): Born in San Francisco, Birnbaum studied mathematics at the University of California at Berkeley, obtaining a Ph.D. degree in mathematical statistics in 1954. His initial research was on classification techniques and discriminant analysis but later he turned to more theoretical topics such as the likelihood principle where he made a number of extremely important contributions. Birnbaum died on 1 July 1976 in London.
Birnbaum-Saunders distribution:
The probability distribution of
where a and f are positive parameters and Z is a random variable with a standard normal distribution. Used in models representing time to failure of material subjected to a cyclically repeated stress. The distribution is given explicitly by
Fig. 16 Biplot of a set of three-dimensional data on 10 individuals.
Birth-cohort study:
A prospective study of people born in a defined period. They vary from large studies that aim to be nationally representative to those that are area based with populations as small as a 1000 subjects. An example is the Avon longitudinal study of births occurring in one English county used to collect data on risk exposure during pregnancy.
Birthdays problem:
The birthdays of r people form a sample of size r from the population of all days in the year. As a first approximation these may be considered as a random selection of birthdays from the year consisting of 365 days. Then the probability, p, that all r birthdays are different is
For example, when r = 23, p < 1, so that for 23 people the probability that no two people have the same birthday is less than 0.5. For 56 people this probability decreases to 0.01.
Birth-death process:
A continuous time Markov chain with infinite state space in which changes of state are always from n to n + 1 or n to n — 1. The state of such a system can be viewed as the size of a population that can increase by one (a ‘birth’) or decrease by one (a ‘death’).
Birth-death ratio:
The ratio of number of births to number of deaths within a given time in a population.
Birth defect registries:
Organized databases containing information on individuals born with specified congenital disorders. Important in providing information that may help to prevent birth defects.
Birth rate:
The number of births occurring in a region in a given time period, divided by the size of the population of the region at the middle of the time period, usually expressed per 1000 population. For example, the birth rates for a number of countries in 1966 were as follows:
| Country | Birth rate/1000 |
| Egypt | 42.1 |
| India | 20.9 |
| Japan | 17.3 |
| Canada | 24.8 |
| USA | 21.7 |
Biserial correlation:
A measure of the strength of the relationship between two variables, one continuous (y) and the other recorded as a binary variable (x), but having underlying continuity and normality. Estimated from the sample values as
where y1 is the sample mean of the y variable for those individuals for whom x = 1 y0 is the sample mean of the y variable for those individuals for whom x = 0, sy is th< standard deviation of the y values, p is the proportion of individuals with x = 1 and q = 1 — p is the proportion of individuals with x = 0. Finally u is the ordinati (height) of the standard normal distribution at the point of division between the and q proportions of the curve. See also point-biserial correlation. [KA2 Chapter 26.
Bisquare regression estimation:
Robust estimation of the parameters f}1, f}2, Pq in th< multiple regression model
The estimators are given explicitly by the solutions of the q equations
where S is the median absolute residual, k is a given positive parameter and
The estimation equations are solved by an iterative process. See also M-estimators.
Bit:
A unit of information, consisting of one binary digit.
Bivar criterion:
A weighted sum of squared bias and variance in which the relative weights reflect the importance attached to these two quantities. Sometimes used for selecting explanatory variables in regression analysis. [Technometrics, 1982, 24, 181-9.]
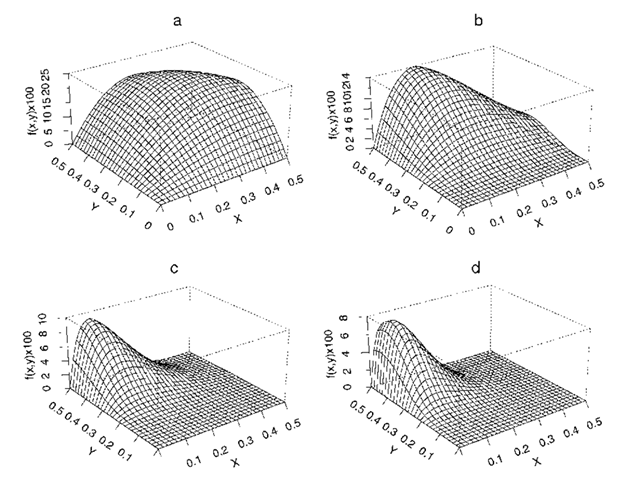
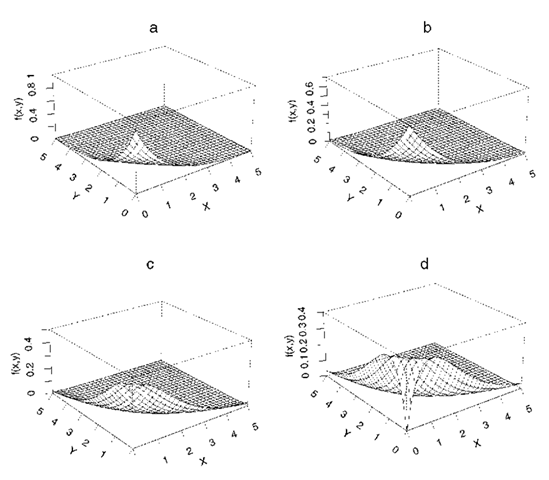
Bivariate beta distribution:
A bivariate distribution, fix, y), given by
where x > 0, y > 0, x + y < 1 and a, fi,y > 0. Perspective plots of a number of such distributions are shown in Fig. 17.
Bivariate boxplot:
A bivariate analogue of the boxplot in which an inner region contains 50% of the data, and a ‘fence’ helps identify potential outliers. Robust methods are generally used to find estimates of the location, scale and correlation parameters required to construct the plot, so as to avoid the possible distortions that outlying obervations may cause. Examples of such plots are shown in Fig. 18.
Bivariate Cauchy distribution:
A bivariate distribution, f (x,y), given by
Perspective plots of a number of such distributions are shown in Fig. 19.
Bivariate data:
Data in which the subjects each have measurements on two variables.
Fig. 17 Perspective plots of four bivariate beta distributions: (a) a = 2, fi = 2, y = 2; (b) a = 2, fi = 4, y = 3; (c) a = 2, fi = 7,y = 6; (d) a = 2, fi = 8, y = 9.
Fig. 18 Bivariate boxplots shown on a draughtsman’s plot of a set of multivariate data.
Bivariate distribution:
The joint distribution of two random variables, x and y. A well known example is the bivariate normal distribution which has the form
Bivariate distribution:
The joint distribution of two random variables, x and y. A well known example is the bivariate normal distribution which has the form
where \x1 ,a1 ,a2 ,p are, respectively, the means, standard deviations and correlation of the two variables. Perspective plots of a number of such distributions are shown in Fig. 20. See also bivariate beta distribution, bivariate Cauchy distribution, bivariate Gumbel distribution and bivariate exponential distribution. [KA1 Chapter 7.]
Fig. 19 Perspective plots of four bivariate Cauchy distributions (a) a = 0.2; (b) a = 1.0; (c) a = 4.0; (d) a = 8.0.
Fig. 20 Perspective plots of four bivariate normal distributions with zero means and unit standard deviations. (a) p = 0.6; (b) p = 0.0; (c) p = 0.3; (d) p = 0.9.
Bivariate exponential distribution:
Any bivariate distribution, f (x, y), that has an exponential distribution for each of its marginal distributions. An example is
Perspective plots of a number of such distributions are shown in Fig. 21.
Bivariate Gumbel distribution:
A bivariate distribution, f (x,y), having the form
where 6 is a parameter which can vary from 0 to 1 giving an increasing positive correlation between the two variables. The distribution is often used to model combinations of extreme environmental variables. A perspective plot of the distribution is shown in Fig. 22. [Statistics in Civil Engineering, 1997, A.V. Metcalfe, Edward Arnold, London.]
Bivariate Oja median:
An alternative to the more common spatial median as a measure of location for bivariate data. Defined as the value of 6 that minimizes the objective function, T(6), given by
where A(a, b, c) is the area of the triangle with vertices a, b, c and x1, x2,…, xn are n bivariate observations.
Fig. 21 Perspective plots of four bivariate exponential distributions (a) a = 0.1; (b) a = 0.3; (c) a = 0.6; (d) a = 1.0.
Fig. 22 Perspective plot of a bivariate Gumbel distribution with 6 = 0.5.
Bivariate Pareto distribution:
A probability distribution useful in the modeling of life times of two-component systems working in a changing environment. The distribution is specified by
where ft < min (xj, x2)<i.
Bivariate Poisson distribution:
A bivariate probability distribution based on the joint distribution of the variables X1 and X2 defined as
where Yj, Y2 and Y12 are mutually independent random variables each having a Poisson distribution with means A1, X2 and X3 respectively. The joint distribution of X1 and X2 is
Bivariate survival data:
Data in which two related survival times are of interest. For example, in familial studies of disease incidence, data may be available on the ages and causes of death of fathers and their sons. [Statistics in Medicine, 1993, 12, 241-8.]
Bjerve, Petter Jakob (1913-2004):
Born in Stjordal, Norway, in 1913, Bjerve studied economics and statistics and after World War II was asked to head an office in the Ministry of Finance in Norway. After studying at the University of Chicago from 1947 to 1949, Bjerve was appointed Director General of Statistics Norway, a position he occupied until 1980. During this time he established Statistics Norway which provided essential information for policy making and planning. Bjerve was influential on the development of statistics in the international arena and served as president of the International Statistics Institute from 1971 to 1974. He died on 12 January 2004.
Black, Arthur (1851-1893):
Born in Brighton, UK, Black took a B.Sc degree of the University of London by private study, graduating in 1877. He earned a rather precarious living as an army coach and tutor in Brighton, while pursuing his mathematical and philosophical interests. He derived the chi-squared distribution as the limit to the multinomial distribution and independently discovered the Poisson distribution. Black’s main aim was to quantify the theory of evolution. He died in January 1893.
Blinder-Oaxacca method:
A method used for assessing the effect of the role of income on the racial wealth gap. The method is based on a decomposition of the mean interrace difference in wealth into the portion due to differences in the distribution of one or more explanatory variables and that due to differences in the conditional expectation function, and the parametric estimation of a wealth-earnings relationship by race. [Journal of Human Resources, 1973, 8, 436-55.]
Blinding:
A procedure used in clinicaltrials to avoid the possible bias that might be introduced if the patient and/or doctor knew which treatment the patient is receiving. If neither the patient nor doctor are aware of which treatment has been given the trial is termed double-blind. If only one of the patient or doctor is unaware, the trial is called single-blind. Clinical trials should use the maximum degree of blindness that is possible, although in some areas, for example, surgery, it is often impossible for an investigation to be double-blind.
Bliss, Chester Ittner (1899-1979):
Born in Springfield, Ohio, Bliss studied entomology at Ohio State University, obtaining a Ph.D. in 1926. In the early 1930s after moving to London he collaborated with Fisher, and did work on probit analysis. After a brief period at the Institute of Plant Protection in Lennigrad, Bliss returned to the United States becoming a biometrician at the Connecticut Agricultural Experimental Station where he remained until his retirement in 1971. He played a major role in founding the International Biometric Society. The author of over 130 papers on various aspects of bioassay. Bliss died in 1979.
BLKL algorithm:
An algorithm for constructing D-optimal designs with specified block size.
Block:
A term used in experimental design to refer to a homogeneous grouping of experimental units (often subjects) designed to enable the experimenter to isolate and, if necessary, eliminate, variability due to extraneous causes. See also randomized block design.
Block, Borges and Savits model:
A model used for recurrent events in reliability and engineering settings. In this model a system (or component) is put on test at time zero. On the system’s failure at some time t, it undergoes a perfect repair with probability p(t) or an imperfect repair with probability q(t) = 1 — p(t). A perfect repair reverts the system’s effective age to zero, whereas a minimal repair leaves the system’s effective age unchanged from that at failure.
Block clustering:
A method of cluster analysis in which the usual multivariate data matrix is partitioned into homogeneous rectangular blocks after reordering the rows and columns. The objectives of the analysis are to identify blocks or clusters of similar data values, to identify clusters of similar rows and columns, and to explore the relationship between the marginal (i.e. rows and column) clusters and the data blocks.
Blocking:
The grouping of plots, or experimental units, into blocks or groups, of homogeneous units. Treatments are then assigned at random to the plots within the blocks. The basic goal is to remove block-to-block variation from experimental error. Treatment comparisons are then made within the blocks on plots that are as nearly alike as possible.
Block randomization:
A random allocation procedure used to keep the numbers of subjects in the different groups of a clinicaltrialclosely balanced at all times. For example, if subjects are considered in sets of four at a time, there are six ways in which two treatments (A and B) can be allocated so that two subjects receive A and two receive B, namely
1.AABB
4.BBAA
2.ABAB
5.BABA
3.ABBA
6.BAAB
If only these six combinations are used for allocating treatments to each block of four subjects, the numbers in the two treatment groups can never, at any time, differ by more than two.
Blomqvist model:
A model for assessing the relationship between severity (level) and rate of change (slope) in a longitudinal study.
BLUE:
Abbreviation for best linear unbiased estimator.
Blunder index:
A measure of the number of ‘gross’ errors made in a laboratory and detected by an external quality assessment exercise.
BLUP:
Abbreviation for best linear unbiased predictor.
BMA:
Abbreviation for Bayesian model averaging.
BMDP:
A large and powerful statistical software package that allows the routine application of many statistical methods including Student’s t-tests, factor analysis, and analysis of variance. Modules for data entry and data management are also available and the package is supported by a number of well-written manuals. Now largely taken over by SPSS.
BMI:
Abbreviation for body mass index.
Body mass index (BMI):
An index defined as weight in kilograms divided by the square of height in metres. An individual with a value less than 20 is generally regarded as underweight, while one with a value over 25 is overweight.
Bonferroni, Carlo Emilio (1892-1960):
Born in Bergamo, Italy, Bonferroni studied mathematics at the University of Turin. In 1932 he was appointed to the Chair of Mathematics of Finance at the University of Bari, and in 1933 moved to the University of Florence where he remained until his death on 18 August 1960. Bonferroni contributed to actuarial mathematics and economics but is most remembered among statisticians for the Bonferroni correction.
Bonferroni correction:
A procedure for guarding against an increase in the probability of a type I error when performing multiple significance tests. To maintain the probability of a type I error at some selected value a, each of the m tests to be performed is judged against a significance level, a/m. For a small number of simultaneous tests (up to five) this method provides a simple and acceptable answer to the problem of multiple testing. It is however highly conservative and not recommended if large numbers of tests are to be applied, when one of the many other multiple comparison procedures available is generally preferable. See also least significant difference test, Newman-Keuls test, Scheffe’s test and Simes modified Bonferroni procedure. [SMR Chapter 9.]
Boole’s inequality:
The following inequality for probabilities:
where the B, are events which are not necessarily mutually exclusive or exhaustive. [KA1 Chapter 8.]
Boosting:
A term used for a procedure which increases the performance of allocation rules in classification problems, by assigning a weight to each observation in the training set which reflects its importance.
Bootstrap:
A data-based simulation method for statistical inference which can be used to study the variability of estimated characteristics of the probability distribution of a set of observations and provide confidence intervals for parameters in situations where these are difficult or impossible to derive in the usual way. (The use of the term bootstrap derives from the phrase ‘to pull oneself up by one’s bootstraps’.) The basic idea of the procedure involves sampling with replacement to produce random samples of size n from the original data, x1, x2,…, xn; each of these is known as a bootstrap sample and each provides an estimate of the parameter of interest. Repeating the process a large number of times provides the required information on the variability of the estimator and an approximate 95% confidence interval can, for example, be derived from the 2.5% and 97.5% quantiles of the replicate values.
Borel-Tanner distribution:
The probability distribution of the number of customers (N) served in a queueing system in which arrivals have a Poisson distribution with parameter X and a constant server time, given that the length of the queue at the initial time is r. Given by
Borrowing effect:
A term used when abnormally low standardized mortalityrates for one or more causes of death may be a reflection of an increase in the proportional mortality rates for other causes of death. For example, in a study of vinyl chloride workers, the overall proportional mortality rate for cancer indicated approximately a 50% excess, as compared with cancer death rates in the male US population. (One interpretation of this is a possible deficit of non-cancer deaths due to the healthy worker effect). Because the overall proportional mortality rate must by definition be equal to unity, a deficit in one type of mortality must entail a ‘borrowing’ from other causes.
Bortkiewicz, Ladislaus von (1868-1931):
Born in St Petersburg, Bortkiewicz graduated from the Faculty of Law at its university. Studied in GOttingen under Lexis eventually becoming Associate Professor at the University of Berlin in 1901. In 1920 he became a full Professor of Economics and Statistics. Bortkiewicz worked in the areas of classical economics, population statistics, acturial science and probability theory. Probably the first statistician to fit the Poisson distribution to the well-known data set detailing the number of soldiers killed by horse kicks per year in the Prussian army corps. Bortkiewicz died on 15 July 1931 in Berlin.
Bose, RajChandra (1901-1987):
Born in Hoshangabad, India, Bose was educated at Punjab University, Delhi University and Calcutta University reading pure and applied mathematics. In 1932 he joined the Indian Statistical Institute under Mahalanobis where he worked on geometrical methods in multivariate analysis. Later he applied geometrical methods to the construction of experimental designs, in particular to balanced incomplete block designs. Bose was Head of the Department of Statistics at Calcutta University from 1945 to 1949, when he moved to the Department of Statistics at the University of North Carolina, USA where he remained until his retirement in 1971. He died on 30 October 1987 in Fort Collins, Colorado, USA.
Boundary estimation:
The problem involved with estimating the boundary between two regions with different distributions when the data consists of independent observations taken at the nodes of a grid. The problem arises in epidemiology, forestry, marine science, meteorology and geology. [Pattern Recognition, 1995, 28, 1599-609.]
Bowker’s test for symmetry:
A test that can be applied to square contingency tables, to assess the hypothesis that the probability of being in cell i, j is equal to the probability of being in cell j, i. Under this hypothesis, the expected frequencies in both cells are (w- + njY)/2 where nij and njY are the corresponding observed frequencies. The test statistic is
Under the hypothesis of symmetry, X has approximately a chi-squared distribution with c(c — 1)/2 degrees of freedom, where c is the number of rows of the table (and the number of columns). In the case of a two-by-two contingency table the procedure is equivalent to McNemar’s test.
Bowley, Arthur Lyon (1869-1957):
Born in Bristol, England, Bowley read mathematics at Cambridge. His first appointment was as a mathematics teacher at St. John’s School, Leatherhead, Surrey where he worked from 1893 to 1899. It was during this period that his interest in statistics developed. Joined the newly established London School of Economics (LSE) in 1895 to give evening courses in statistics. In 1919 Bowley was elected to a newly-established Chair of Statistics at LSE, a post he held until his retirement in 1936. He made important contributions to the application of sampling techniques to economic and social surveys and produced a famous text topic, Elements of Statistics, which was first published in 1910 and went through seven editions up to 1937. Bowley was President of the Royal Statistical Society in 19381940, and received the Society’s Guy medals in silver in 1895 and in gold in 1935. He died on 21 January 1957 in Haslemere, Surrey, England.
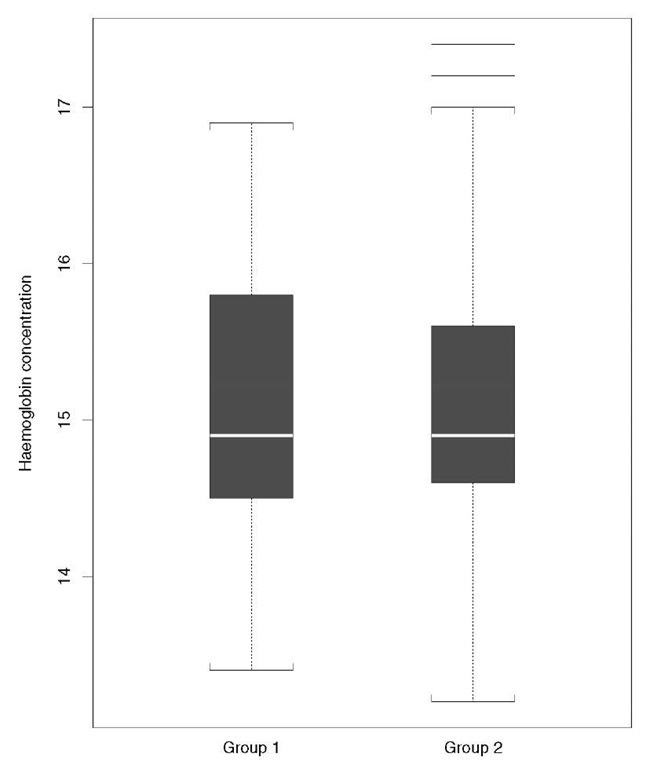
Box-and-whisker plot:
A graphical method of displaying the important characteristics of a set of observations. The display is based on the five-number summary of the data with the ‘ box’ part covering the inter-quartile range, and the ‘whiskers’ extending to include all but outside observations, these being indicated separately. Often particularly useful for comparing the characteristics of different samples as shown in Fig. 23.
Box-Behnken designs:
A class of experimental designs that are constructed by combining two-level factorial designs with balanced incomplete block designs.
Box-counting method:
A method for estimating the fractal dimension of self-similar patterns in space which consists of plotting the number of pixels which intersect the pattern under consideration, versus length of the pixel unit.
Box-Cox transformation:
A family of data transformations designed to achieve normality and given by
Fig. 23 Box-and-whisker plot of haemoglobin concentration for two groups of men.
Maximum likelihood estimation can be used to estimate a suitable value of X for a particular variable. See also Taylor’s power law and Box-Tidwell transformation.
Box-Jenkins models:
Synonym for autoregressive moving average models.
Box-Miiller transformation:
A method of generating random variables from a normal distribution by using variables from a uniform distribution in the interval (0,1). Specifically if U1 and U2 are random uniform (0,1) variates then
are independent standard normal variables. Often used for generating data from a normal distribution when using simulation.
Box-Pierce test:
A test to determine whether time series data are simply a white noise sequence and that therefore the observations are not related. The test statistic is
where rk, k = 1, 2,…, m, are the values of the autocorrelations up to lag m and n is the number of observations in the series. If the data are a white noise series then Qm has a chi-squared distribution with m degrees of freedom. The test is valid only if m is very much less than n.
Boxplot:
Synonym for box-and-whisker plot.
Box’s test:
A test for assessing the equality of the variances in a number of populations that is less sensitive to departures from normality than Bartlett’s test. See also Hartley’s test.
Bradley, Ralph (1923-2001):
Born in Smith Falls, Ontario, Canada, Bradley received an honours degree in mathematics and physics from Queen’s University, Canada in 1944. After war service he took an M.A. in mathematics and statistics in 1946 and in 1949 completed his Ph.D. studies at the University of North Carolina at Chapel Hill. While working at Virginia Polytechnic Institute he collaborated with Milton Terry on a statistical test for paired comparisons, the Bradley-Terry model. Bradley also made contributions to nonparametric statistics and multivariate methods. He died on 30 October 2001 in Athens, Georgia, USA.
Bradley-Terry model:
A model for experiments in which responses are pairwise rankings of treatments (a paired comparison experiment), which assigns probabilities to each of (2) pairs among t treatments in terms of t — 1 parameters, k1,k2,… ,xt, Ki > 0, i = 1,…, t associated with treatments T1,…, Tt. These parameters represent relative selection probabilities for the treatments subject to the constraints Ki > 0 and J]t= 1 K = 1. The probability that treatment Ti is preferred over treatment Tj in a single comparison is Ki+ Kj). Maximum likelihood estimators for the ks can be found from observations on the number of times treatment Ti is preferred to treatment Tj in a number of comparisons of the two treatments. [Biometrics, 1976, 32, 213-32.]
Branch-and-bound algorithm:
Synonym for leaps-and-bounds algorithm.
Branching process:
A process involving a sequence of random variables Y1, Y2,…, Yn where Yk is the number of particles in existence at time k and the process of creation and annihilation of particles is as follows: each particle, independently of the other particles and of the previous history of the process, is transformed into j particles with probability pj, j = 0,1,…, M. Used to describe the evolution of populations of individuals, which reproduce independently. A particularly interesting case is that in which each particle either vanishes with probability q or divides into two with probability p, p + q = 1. In this case it can be shown that pj = Pr(Yk+1 = j\ Yk = i) is given by
Brass, William (1921-99): Born in Edinburgh, Brass studied at Edinburgh University, first from 1940 to 1943 and then again, after serving in World War II, from 1946 to 1947. In 1948 he joined the East African Statistical Department as a statistician and later became its Director. It was during his seven years in these posts that Brass developed his ideas on both the collection and analysis of demographic data. In 1955 he joined the Department of Statistics in Aberdeen University where he remained for the next nine years, years in which, in collaboration with several others, he produced The Demography of Tropical Africa, which remained the definitive work on the subject for the next decade. From 1965 until his retirement in 1988 he worked at the London School of Tropical Medicine and Hygiene. Brass made major contributions to the study of the biosocial determinants of fertility and mortality, population forecasting and the evaluation of family planning programmes.
Breakdown point:
A measure of the insensitivity of an estimator to multiple outliers in the data. Roughly it is given by the smallest fraction of data contamination needed to cause an arbitrarily large change in the estimate.
Breiman, Leo (1928-2005):
Breiman was born in New York City but moved to California when he was five years old. He graduated from Roosevelt High School in 1945 and in 1949 earned a degree in physics from the California Institute of Technology. Breiman then joined Columbia University intending to study philosophy, but changed to mathematics, receiving a master’s degree in 1950. In 1954 he was awarded a Ph.D. from the University of California, Berkeley, and then began to teach probability theory at UCLA. Several years later he resigned from the university and earned a living as a statistical consultant before rejoining the university world at Berkeley where he established the Statistical Computing Facility. Breiman’s main work in statistics was in the area of computationally intensive multivariate analysis and he is best known for his contribution to classification and regression trees. Leo Breiman died on 5 July 2005.
Breslow-Day test:
A test of the null hypothesis of homogeneity of the odds ratio across a series of 2×2 contingency tables.
Breslow’s estimator:
An estimator of the cumulative hazard function in survival analysis.
Brier score:
The mean squared error for binary data, measuring the difference between a predicted probability of an event and its occurrence expressed as 0 or 1 depending on whether or not the event has occurred.
Brown-Forsythe test:
A procedure for assessing whether a set of population variances are equal, based on applying an F-test to the following values calculated for a sample of observations from each of the populations;
Zij = | Xij — m. |
where x j is the jth observation in the ith group and m . is the median of the ith group. See also Box’s test, Bartlett’s test and Hartley’s test.
Brownian motion:
A stochastic process, Xt, with state space the real numbers, satisfying
• X0 = 0;
• for any s1 < t1 < s2 < t2 <• • • < sn < tn, the random variables Xt — ,…, Xt — XSn are independent;
• for any s < t, the random variable Xt — Xs has a normal distribution with mean 0 and variance (t — s)a2.
Brushing scatterplots:
An interactive computer graphics technique sometimes useful for exploring multivariate data. All possible two-variable scatterplots are displayed, and the points falling in a defined area of one of them (the ‘brush’) are highlighted in all. See also dynamic graphics.
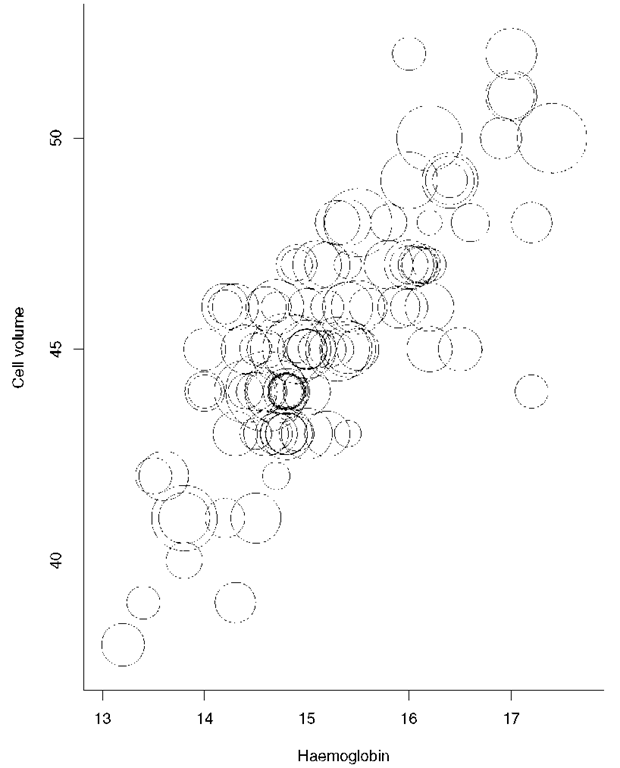
Bubble plot:
A method for displaying observations which involve three variable values. Two of the variables are used to form a scatter diagram and values of the third variable are represented by circles with differing radii centred at the appropriate position. An example is given in Fig. 24.
Buckley-James method:
An iterative procedure for obtaining estimates of regression coefficients in models involving a response variable that is right-censored.
Buehler confidence bound:
An upper confidence bound for a measure of reliability/maintainability of a series system in which component repair is assumed to restore the system to its original status.
Buffon’s needle problem:
A problem proposed and solved by Comte de Buffon in 1777 which involves determining the probability, p, that a needle of length l will intersect a line when thrown at random onto a horizontal plane that is ruled with parallel lines a distance a > I apart. The solution is
Can be used to evaluate n since if the needle is tossed N times independently and v.- = 1 if it intersects a line on the ith toss and 0 otherwise then
Fig. 24 Bubble plot of haemoglobin concentrates versus cell volume with radii of circles proportional to white blood count.
In 1850 R.Wolf (an astronomer in Zurich) threw a needle 5000 times and obtained the value 3.1596 for n.
BUGS:
Bayesian inference Using Gibbs Sampling, a software package that provides a means of analysing complex models from a description of their structure provided by the user and automatically deriving the expressions for the Gibbs sampling needed to obtain the posterior marginal distributions. The software is capable of handling a wide range of problems, including hierarchical random effects and measurement errors in generalized linear models, latent variable and mixture models, and various forms of missing and censored data.
Bump hunting:
A colourful term for the examination of frequency distributions for local maxima or modes that might be indicative of separate groups of subjects. See also bimodal distribution, finite mixture distribution and dip test.
Burn-in:
A term used in Markov chain Monte Carlo methods to indicate the necessary period of iterations before samples from the required distribution are achieved.
Burr distributions:
A family of probability distributions which is very flexible and can have a wide range of shapes. The distribution involves two parameters 0 and X and is given explicitly as
Bursty phenomena:
A term sometimes applied to phenomena that exhibit occasional unusually large observations.
Burt matrix:
A matrix used in correspondence analysis when applied to contingency tables with more than two dimensions.
Butler statistic:
A statistic that can be used to test whether a distribution is symmetric about some point.
Byar, D.P. (1938-1991):
Born in Lockland, Ohio, Byar graduated from Harvard Medical School in 1964. Working at the Armed Forces Institute of Pathology, Byar became increasingly interested in the sources of variation in laboratory experiments and the statistical methods for coping with them. After joining the National Cancer Institute in 1968 he became a leading methodologist in clinical trials. Byar died on 5 August 1991 in Washington DC.
Byte:
A unit of information, as used in digital computers, equals eight bits.