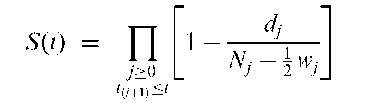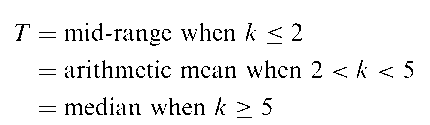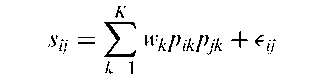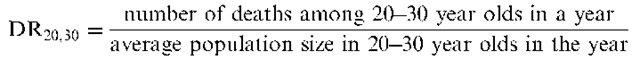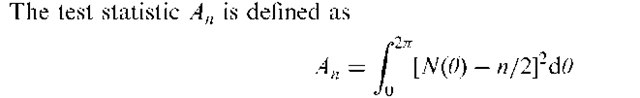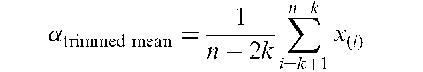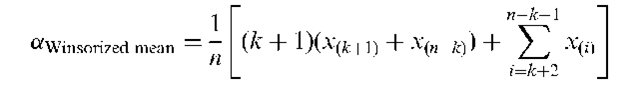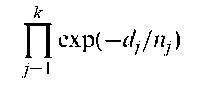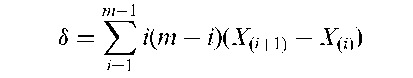Aalen-Johansen estimator:
An estimator of the survival function for a set of survival times, when there are competing causes of death. Related to the Nelson-Aalen estimator.
Aalen’s linear regression model:
A model for the hazard function of a set of survival times given by
where a(t) is the hazard function at time t for an individual with covariates z(t)’ = [z1 (t),..., zp(t)]. The ‘parameters’ in the model are functions of time with a0(t) the baseline hazard corresponding to z(t) = 0 for all t, and aq(t), the excess rate at time t per unit increase in zq(t). See also Cox’s proportional hazards model.
Abbot’s formula:
A formula for the proportion of animals (usually insects) dying in a toxicity trial that recognizes that some insects may die during the experiment even when they have not been exposed to the toxin, and among those who have been so exposed, some may die of natural causes. Explicitly the formula is
where pt is the observable response proportion, pt is the expected proportion dying at a given dose and n is the proportion of insects who respond naturally. [Modelling Binary Data, 2nd edition, 1993, D. Collett, Chapman and Hall/CRC Press, London.]
ABC method:
Abbreviation for approximate bootstrap confidence method.
Absolute deviation:
Synonym for average deviation.
Absolute risk:
Synonym for incidence
Absorption distributions:
Probability distributions that represent the number of ‘individuals’ (e.g. particles) that fail to cross a specified region containing hazards of various kinds. For example, the region may simply be a straight line containing a number of ‘absorption’ points. When a particle travelling along the line meets such a point, there is a probability p that it will be absorbed. If it is absorbed it fails to make any further progress, but also the point is incapable of absorbing any more particles.
Abundance matrices:
Matrices that occur in ecological applications. They are essentially two-dimensional tables in which the classifications correspond to site and species.
Accelerated failure time model:
A general model for data consisting of survival times, in which explanatory variables measured on an individual are assumed to act multi-plicatively on the time-scale, and so affect the rate at which an individual proceeds along the time axis. Consequently the model can be interpreted in terms of the speed of progression of a disease. In the simplest case of comparing two groups of patients, for example, those receiving treatment A and those receiving treatment B, this model assumes that the survival time of an individual on one treatment is a multiple of the survival time on the other treatment; as a result the probability that an individual on treatment A survives beyond time t is the probability that an individual on treatment B survives beyond time 0t, where 0 is an unknown positive constant. When the end-point of interest is the death of a patient, values of 0 less than one correspond to an acceleration in the time of death of an individual assigned to treatment A, and values of 0 greater than one indicate the reverse. The parameter 0 is known as the acceleration factor.
Acceptable risk:
The risk for which the benefits of a particular medical procedure are considered to outweigh the potential hazards.
Acceptance region:
A term associated with statistical significance tests, which gives the set of values of a test statisticfor which the null hypothesis is to be accepted. Suppose, for example, a z-test is being used to test the null hypothesis that the mean blood pressure of men and women is equal against the alternative hypothesis that the two means are not equal. If the chosen significance of the test is 0.05 then the acceptance region consists of values of the test statistic z between -1.96 and 1.96.
Acceptance-rejection algorithm:
An algorithm for generating random numbers from some probability distribution, f (x), by first generating a random number from some other distribution, g(x), where f and g are related by
with k a constant. The algorithm works as follows:
• let r be a random number from g(x);
• let s be a random number from a uniform distribution on the interval (0,1);
• calculate c = ksg(r);
• if c > f (r) reject r and return to the first step; if c < f (r) accept r as a random number.
Acceptance sampling:
A type of quality control procedure in which a sample is taken from a collection or batch of items, and the decision to accept the batch as satisfactory, or reject them as unsatisfactory, is based on the proportion of defective items in the sample. [Quality Control and Industrial Statistics, 4th edition, 1974, A.J. Duncan, R.D. Irwin, Homewood, Illinois.]
Accident proneness:
A personal psychological factor that affects an individual’s probability of suffering an accident. The concept has been studied statistically under a number of different assumptions for accidents:
• pure chance, leading to the Poisson distribution;
• true contagion, i.e. the hypothesis that all individuals initially have the same probability of having an accident, but that this probability changes each time an accident happens;
• apparent contagion, i.e. the hypothesis that individuals have constant but unequal probabilities of having an accident.
The study of accident proneness has been valuable in the development of particular statistical methodologies, although in the past two decades the concept has, in general, been out of favour; attention now appears to have moved more towards risk evaluation and analysis. [Accident Proneness, 1971, L. Shaw and H.S. Sichel, Pergamon Press, Oxford.]
Accidentally empty cells:
Synonym for sampling zeros.
Accrual rate:
The rate at which eligible patients are entered into a clinical trial, measured as persons per unit of time. Often disappointingly low for reasons that may be both physician and patient related.
Accuracy:
The degree of conformity to some recognized standard value. See also bias.
ACE:
Abbreviation for alternating conditional expectation.
ACE model:
A genetic epidemiological model that postulates additive genetic factors, common environmental factors, and specific environmental factors in a phenotype. The model is used to quantify the contributions of genetic and environmental influences to variation.
ACES:
Abbreviation for active control equivalence studies.
ACF:
Abbreviation for autocorrelation function.
ACORN:
An acronym for ‘A Classification of Residential Neighbourhoods’. It is a system for classifying households according to the demographic, employment and housing characteristics of their immediate neighbourhood. Derived by applying cluster analysis to 40 variables describing each neighbourhood including age, class, tenure, dwelling type and car ownership. [Statistics in Society, 1999, D. Dorling and S. Simpson eds., Arnold, London.]
Acquiescence bias:
The bias produced by respondents in a survey who have the tendency to give positive responses, such as ‘true’, ‘like’, ‘often’ or ‘yes’ to a question. At its most extreme, the person responds in this way irrespective of the content of the item. Thus a person may respond ‘true’ to two items like ‘I always take my medication on time’ and ‘I often forget to take my pills’. See also end-aversion bias.
Active control equivalence studies (ACES):
Clinical trials in which the object is simply to show that the new treatment is at least as good as the existing treatment. Such studies are becoming more widespread due to current therapies that reflect previous successes in the development of new treatments. Such studies rely on an implicit historical control assumption, since to conclude that a new drug is efficacious on the basis of this type of study requires a fundamental assumption that the active control drug would have performed better than a placebo, had a placebo been used in the trial.
Active control trials:
Clinical trials in which the trial drug is compared with some other active compound rather than a placebo.
Active life expectancy (ALE):
Defined for a given age as the expected remaining years free of disability. A useful index of public health and quality of life for populations. A question of great interest is whether recent trends towards longer life expectancy have been accompanied by a comparable increase in ALE. [New England Journal of Medicine, 1983, 309, 1218-24.]
Activ Stats:
A commercial computer-aided learning package for statistics. See also statistics for the terrified.
Actuarial estimator:
An estimator of the survival function, S(t), often used when the data are in grouped form. Given explicitly by
where the ordered survival times are 0 < tp-j < ••• < t^-j, N is the number of people at risk at the start of the interval t^-, t(i+1-j, d, is the observed number of deaths in the interval and w the number of censored observations in the interval. [Survival Models and Data Analysis, 1999, R.G. Elandt-Johnson and N.L. Johnson, Wiley, New York.]
Actuarial statistics:
The statistics used by actuaries to evaluate risks, calculate liabilities and plan the financial course of insurance, pensions, etc. An example is life expectancy for people of various ages, occupations, etc.
Adaptive cluster sampling:
A procedure in which an initial set of subjects is selected by some sampling procedure and, whenever the variable of interest of a selected subject satisfies a given criterion, additional subjects in the neighbourhood of that subject are added to the sample.
Adaptive designs:
Clinical trials that are modified in some way as the data are collected within the trial. For example, the allocation of treatment may be altered as a function of the response to protect patients from ineffective or toxic doses.
Adaptive methods:
Procedures that use various aspects of the sample data to select the most appropriate type of statistical method for analysis. An adaptive estimator, T, for the centre of a distribution, for example, might be
where k is the sample kurtosis. So if the sample looks as if it arises from a short-tailed distribution, the average of the largest and smallest observations is used; if it looks like a long-tailed situation the median is used, otherwise the mean of the sample is calculated. [Journal of the American Statistical Association, 1967, 62, 1179-86.]
Adaptive sampling design:
A sampling design in which the procedure for selecting sampling units on which to make observations may depend on observed values of the variable of interest. In a survey for estimating the abundance of a natural resource, for example, additional sites (the sampling units in this case) in the vicinity of high observed abundance may be added to the sample during the survey. The main aim in such a design is to achieve gains in precision or efficiency compared to conventional designs of equivalent sample size by taking advantage of observed characteristics of the population. For this type of sampling design the probability of a given sample of units is conditioned on the set of values of the variable of interest in the population. [Adaptive Sampling, 1996, S.K. Thompson and G.A.F. Seber, Wiley, New York.]
Added variable plot:
A graphical procedure used in all types of regression analysis for identifying whether or not a particular explanatory variable should be included in a model, in the presence of other explanatory variables. The variable that is the candidate for inclusion in the model may be new or it may simply be a higher power of one currently included. If the candidate variable is denoted x, then the residuals from the regression of the response variable on all the explanatory variables, save x, are plotted against the residuals from the regression of x on the remaining explanatory variables. A strong linear relationship in the plot indicates the need for xt in the regression equation (Fig. 1).
Fig. 1 Added variable plot indicating a variable that could be included in the model.
Addition rule for probabilities: For two events, A and B that are mutually exclusive, the probability of either event occurring is the sum of the individual probabilities, i.e.
where Pr(A) denotes the probability of event A etc. For k mutually exclusive events A1, A2,…, Ak, the more general rule is
Additive clustering model: A model for cluster analysis which attempts to find the structure of a similarity matrix with elements Sj by fitting a model of the form
where K is the number of clusters and wk is a weight representing the salience of the property corresponding to cluster k. If object i has the property of cluster k, then pik = 1, otherwise it is zero. [Psychological Review, 1979, 86, 87-123.]
Additive effect:
A term used when the effect of administering two treatments together is the sum of their separate effects. See also additive model.
Additive genetic variance:
The variance of a trait due to the main effects of genes. Usually obtained by a factorial analysisofvariance of trait values on the genes present at one or more loci.
Additive model:
A model in which the explanatory variables have an additive effect on the response variable. So, for example, if variable A has an effect of size a on some response measure and variable B one of size b on the same response, then in an assumed additive model for A and B their combined effect would be a + b.
Additive outlier:
A term applied to an observation in a time series which is affected by a non-repetitive intervention such as a strike, a war, etc. Only the level of the particular observation is considered affected. In contrast an innovational outlier is one which corresponds to an extraordinary shock at some time point T which also influences subsequent observations in the series.
Additive tree:
A connected, undirected graph where every pair of nodes is connected by a unique path and where the distances between the nodes are such that
Additive tree:
A connected, undirected graph where every pair of nodes is connected by a unique path and where the distances between the nodes are such that
An example of such a tree is shown in Fig. 2. See also ultrametric tree.
Adequate subset:
A term used in regression analysis for a subset of the explanatory variables that is thought to contain as much information about the response variable as the complete set. See also selection methods in regression.
Adjacency matrix:
A matrix with elements, xij, used to indicate the connections in a directed graph. If node i relates to node j, xij = 1, otherwise xij = 0. For a simple graph with no self-loops, the adjacency matrix must have zeros on the diagonal. For an undirected graph the adjacency matrix is symmetric.
Fig. 2 An example of an additive tree.
Adjusted correlation matrix:
A correlation matrix in which the diagonal elements are replaced by communalities. The basis of principal factor analysis.
Adjusted treatment means:
Usually used for estimates of the treatment means in an analysis of covariance, after adjusting all treatments to the same mean level for the co-variate(s), using the estimated relationship between the covariate(s) and the response variable.
Adjusting for baseline:
The process of allowing for the effect of baseline characteristics on the response variable usually in the context of a longitudinal study. A number of methods might be used, for example, the analysis of simple change scores, the analysis of percentage change, or, in some cases, the analysis of more complicated variables. In general it is preferable to use the adjusted variable that has least dependence on the baseline measure. For a longitudinal study in which the correlations between the repeated measures over time are moderate to large, then using the baseline values as covariates in an analysis of covariance is known to be more efficient than analysing change scores. See also baseline balance.
Administrative databases:
Databases storing information routinely collected for purposes of managing a health-care system. Used by hospitals and insurers to examine admissions, procedures and lengths of stay.
Admissibility:
A very general concept that is applicable to any procedure of statistical inference. The underlying notion is that a procedure is admissible if and only if there does not exist within that class of procedures another one which performs uniformly at least as well as the procedure in question and performs better than it in at least one case. Here ‘uniformly’ means for all values of the parameters that determine the probability distribution of the random variables under investigation.
Admixture in human populations:
The inter-breeding between two or more populations that were previously isolated from each other for geographical or cultural reasons. Population admixture can be a source of spurious associations between diseases and alleles that are both more common in one ancestral population than the others. However, populations that have been admixed for several generations may be useful for mapping disease genes, because spurious associations tend to be dissipated more rapidly than true associations in successive generations of random mating.
Adoption studies:
Studies of the rearing of a nonbiological child in a family. Such studies have played an important role in the assessment of genetic variation in human and animal traits.
Aetiological fraction:
Synonym for attributable risk.
Affine invariance:
A term applied to statistical procedures which give identical results after the data has been subjected to an affine transformation. An example is Hotelling’s T2 test.
Affine transformation:
The transformation, Y = AX + b where A is a nonsingular matrix and b is any vector of real numbers. Important in many areas of statistics particularly multivariate analysis.
Age-dependent birth and death process:
A birth and death process where the birth rate and death rate are not constant over time, but change in a manner which is dependent on the age of the individual.
Age heaping:
A term applied to the collection of data on ages when these are accurate only to the nearest year, half year or month. Occurs because many people (particularly older people) tend not to give their exact age in a survey. Instead they round their age up or down to the nearest number that ends in 0 or 5. See also coarse data and Whipple index.
Age-period-cohort model:
A model important in many observational studies when it is reasonable to suppose that age, number of years exposed to risk factor, and age when first exposed to risk factor, all contribute to disease risk. Unfortunately all three factors cannot be entered simultaneously into a model since this would result in collinearity, because ‘age first exposed to risk factor’ + ‘years exposed to risk factor’ is equal to ‘age’. Various methods have been suggested for disentangling the dependence of the factors, although most commonly one of the factors is simply not included in the modelling process. See also Lexis diagram.
Age-related reference ranges:
Ranges of values of a measurement that give the upper and lower limits of normality in a population according to a subject’s age.
Age-specific death rates:
Death rates calculated within a number of relatively narrow age bands. For example, for 20-30 year olds,
Calculating death rates in this way is usually necessary since such rates almost invariably differ widely with age, a variation not reflected in the crude death rate. See also cause-specific death rates and standardized mortality ratio.
Age-specific failure rate:
A synonym for hazard function when the time scale is age.
Age-specific incidence rate:
Incidence rates calculated within a number of relatively narrow age bands. See also age-specific death rates.
Agglomerative hierarchical clustering methods:
Methods of clusteranalysis that begin with each individual in a separate cluster and then, in a series of steps, combine individuals and later, clusters, into new, larger clusters until a final stage is reached where all individuals are members of a single group. At each stage the individuals or clusters that are ‘closest’, according to some particular definition of distance are joined. The whole process can be summarized by a dendrogram. Solutions corresponding to particular numbers of clusters are found by ‘cutting’ the dendrogram at the appropriate level. See also average linkage, complete linkage, single linkage, Ward’s method, Mojena’s test, K-means cluster analysis and divisive methods.
Agresti’s a:
A generalization of the odds ratio for 2×2 contingency tables to larger contingency tables arising from data where there are different degrees of severity of a disease and differing amounts of exposure.
Agronomy trials:
A general term for a variety of different types of agricultural field experiments including fertilizer studies, time, rate and density of planting, tillage studies, and pest and weed control studies. Because the response to changes in the level of one factor is often conditioned by the levels of other factors it is almost essential that the treatments in such trials include combinations of multiple levels of two or more production factors.
AI:
Abbreviation for artificial intelligence.
AIC:
Abbreviation for Akaike’s information criterion.
Aickin’s measure of agreement:
A chance-corrected measure of agreement which is similar to the kappa coefficient but based on a different definition of agreement by chance.
AID: Abbreviation for automatic interaction detector.
Aitchison distributions:
A broad class of distributions that includes the Dirichlet distribution and logistic normal distributions as special cases.
Aitken, Alexander Craig (1895-1967):
Born in Dunedin, New Zealand, Aitken first studied classical languages at Otago University, but after service during the First World War he was given a scholarship to study mathematics in Edinburgh. After being awarded a D.Sc., Aitken became a member of the Mathematics Department in Edinburgh and in 1946 was given the Chair of Mathematics which he held until his retirement in 1965. The author of many papers on least squares and the fitting of polynomials, Aitken had a legendary ability at arithmetic and was reputed to be able to dictate rapidly the first 707 digits of n. He was a Fellow of the Royal Society and of the Royal Society of Literature. Aitken died on 3 November 1967 in Edinburgh.
Ajne’s test:
A distribution free method for testing the uniformity of a circular distribution.
where N(0) is the number of sample observations that lie in the semicircle, 0 to 0 + n. Values close to zero lead to acceptance of the hypothesis of uniformity. [Scandinavian Audiology, 1996, 201-6.]
Akaike’s information criterion (AIC):
An index used in a number of areas as an aid to choosing between competing models. It is defined as
-2Lm + 2m
where Lm is the maximized log-likelihood and m is the number of parameters in the model. The index takes into account both the statistical goodness of fit and the number of parameters that have to be estimated to achieve this particular degree of fit, by imposing a penalty for increasing the number of parameters. Lower values of the index indicate the preferred model, that is, the one with the fewest parameters that still provides an adequate fit to the data. See also parsimony principle and Schwarz’s criterion.
ALE:
Abbreviation for active life expectancy.
Algorithm:
A well-defined set of rules which, when routinely applied, lead to a solution of a particular class of mathematical or computational problem.
Allele:
The DNA sequence that exists at a genetic location that shows sequence variation in a population. Sequence variation may take the form of insertion, deletion, substitution, or variable repeat length of a regular motif, for example, CACACA.
Allocation ratio:
Synonym for treatment allocation ratio.
Allometry:
The study of changes in shape as an organism grows.
All subsets regression:
A form of regression analysis in which all possible models are considered and the ‘best’ selected by comparing the values of some appropriate criterion, for example, Mallow’s Ck statistic, calculated on each. If there are q explanatory variables, there are a total of 2q – 1 models to be examined. The leaps-and-bounds algorithm is generally used so that only a small fraction of the possible models have to be examined. See also selection methods in regression.
Almon lag technique:
A method for estimating the coefficients, fi0, f}1,…, f}r, in a model of the form
where yt is the value of the dependent variable at time t, xt,…, xt—r are the values of the explanatory variable at times t, t — 1,…, t — r and et is a disturbance term at time t. If r is finite and less than the number of observations, the regression coefficients can be found by least squares estimation. However, because of the possible problem of a high degree of multicollinearity in the variables xt,…, xt—r the approach is to estimate the coefficients subject to the restriction that they lie on a polynomial of degree p, i.e. it is assumed that there exist parameters A,0, A1,… ,Xp such that
This reduces the number of parameters from r + 1 to p + 1. When r = p the technique is equivalent to least squares. In practice several different values of r and/or p need to be investigated.
Alpha(a):
The probability of a type I error. See also significance level.
Alpha factoring:
A method of factor analysis in which the variables are considered samples from a population of variables.
Alpha spending function:
An approach to interim analysis in a clinical trial that allows the control of the type I error rate while giving flexibility in how many interim analyses are to be conducted and at what time.
Alpha(a)-trimmed mean:
A method of estimating the mean of a population that is less affected by the presence of outliers than the usual estimator, namely the sample average. Calculating the statistic involves dropping a proportion a (approximately) of the observations from both ends of the sample before calculating the mean of the remainder. If x^, x^,…, x^ represent the ordered sample values then the measure is given by
where k is the smallest integer greater than or equal to an. See also M-estimators.
Alpha(a)-Winsorized mean:
A method of estimating the mean of a population that is less affected by the presence of outliers than the usual estimator, namely the sample average. Essentially the k smallest and k largest observations, where k is the smallest integer greater than or equal to an, are respectively increased or reduced in size to the next remaining observation and counted as though they had these values. Specifically given by
where x^, xp-j,…, x^ are the ordered sample values. See also M-estimators.
Alshuler’s estimator:
An estimator of the survival function given by
where dj is the number of deaths at time j nj the number of individuals alive just before tj and t^ < tp- < ••• < t^ are the ordered survival times. See also product limit estimator.
Alternate allocations:
A method of allocating patients to treatments in a clinical trial in which alternate patients are allocated to treatment A and treatment B. Not to be recommended since it is open to abuse.
Alternating conditional expectation (ACE):
A procedure for estimating optimal transformations for regression analysis and correlation. Given explanatory variables x1,…, xq and response variable y, the method finds the transformations g(y) and s1(x1),…, sq(xq) that maximize the correlation between y and its predicted value. The technique allows for arbitrary, smooth transformations of both response and explanatory variables.
Alternating least squares:
A method most often used in some methods of multidimensional scaling, where a goodness-of-fiit measure for some confiiguration of points is minimized in a series of steps, each involving the application of least squares.
Alternating logistic regression:
A method of logistic regression used in the analysis of longitudinal data when the response variable is binary. Based on generalized estimating equations.
Alternative hypothesis:
The hypothesis against which the null hypothesis is tested.
Aly’s statistic:
A statistic used in a permutation test for comparing variances, and given by
where X(1) < X(2) < ••• < X(m) are the order statistics of the first sample. [Statistics and Probability Letters, 1990, 9, 323-5.]
Amersham model:
A model used for dose-response curves in immunoassay and given by y =100(2(1 – fa)02)/(fi3 + h + A + x + [(& – $2 + A + x)2 + 2) + A where y is percentage binding and x is the analyte concentration. Estimates of the four parameters, >h3>h4> may be obtained in a variety of ways.
AML:
Abbreviation for asymmetric maximum likelihood.
Amplitude:
A term used in relation to time series, for the value of the series at its peak or trough taken from some mean value or trend line.
Analysis as-randomized:
Synonym for intention-to-treat analysis.
Analysis of covariance (ANCOVA):
Originally used for an extension of the analysis of variance that allows for the possible effects of continuous concomitant variables (covariates) on the response variable, in addition to the effects of the factor or treatment variables. Usually assumed that covariates are unaffected by treatments and that their relationship to the response is linear. If such a relationship exists then inclusion of covariates in this way decreases the error mean square and hence increases the sensitivity of the F-tests used in assessing treatment differences. The term now appears to also be more generally used for almost any analysis seeking to assess the relationship between a response variable and a number of explanatory variables. See also parallelism in ANCOVA and generalized linear models.