The difficulties in maneuvering a vehicle through space are not intuitively obvious to someone who has not been involved in the field. After all, we have been exposed to the television and movie concepts of space travel, wherein there seems to be almost unlimited electrical power, rocket thrust, and propellant, and the protagonist simply flies off to a distant moon or planet using visual references for navigation.
Actually, the finite limits of electrical energy, thrust, and propellant on a vehicle are the driving forces that demand efficient and accurate equipment to perform the functions of steering and navigation while keeping the vehicle attitude stabilized. Added to these restrictions are the needs for minimum volume and mass. An intricate system results that is extremely difficult to design, construct, and test and usually is one of the most expensive on the vehicle.
Terminology
As in most fields, the space industry has a set of terms and definitions peculiar to the field that, unfortunately, are not always consistent in meaning. The term ”guidance system” is sometimes used interchangeably for ”guidance and navigation system” or ”guidance, navigation, and control system” or ”guidance and control system.” In this article, the terms are used as follows:
Guidance means the actual steering of the vehicle as it travels through space. Guidance commands may originate from a crew onboard, from an onboard computer, or from external sources via radio commands. In addition, if the thrust of a space vehicle is variable and controllable, the command for modulating the thrust is usually a guidance function.
Navigation is the measurement of the location of the vehicle in space and plotting the course of the vehicle. Navigational fixes may come from onboard human sightings using telescopes and sextants, from automatic onboard star or horizon sensors, or from radio/radar tracking equipment on the ground.
Control refers to the spatial alignment and stabilization of the vehicle while the guidance and navigation functions are being performed, and includes onboard processing and routing of commands to the devices (typically thrusters, reaction wheels, control moment gyroscopes, or aerodynamic surfaces), termed effectors, that produce reactive forces on the vehicle.
The combination of these three functions into one system results in the integrated guidance, navigation, and control system, or simply the GN&C system.
Space Guidance
As mentioned earlier, the finite limits of electrical energy, thrust, and propellant on a space vehicle are the reasons one simply cannot point the vehicle toward the target and fly it there. Further, within the Universe, the target itself is typically moving, and if the spacecraft were simply steered toward it, the spacecraft could end up chasing it. The situation is analogous to that of a shot gunner who must ”lead” the target, that is, aim at a point on the flight path ahead of the target so that the shot arrives at the point where the target will be rather than the point where it was when the trigger was pulled. Other complicating factors are the effects of the gravity of Earth, the Moon, the Sun, and the planets, as well as their individual rotations if the launch points or landing sites lie on the surface.
A typical spacecraft trajectory that results from these conditions has the following characteristics:
* The launch point is on a rotating Earth (or Moon or planet).
* The gravitational pull of Earth and the Moon are significant effects.
* The flight path is curved and is likely to be nonplanar.
* The flight duration may be anywhere from minutes to years.
* The flight path is carefully plotted and optimized during mission planning.
The guidance function steers the spacecraft along the preplanned flight path while accommodating these characteristics.
To understand the guidance function better, consider the following hypothetical mission trajectory:
1. Launch occurs at Cape Canaveral, Florida, U.S.A. The flight path bends from a vertical ascent to a due easterly direction. As orbital altitude, say 200 nautical miles, is achieved, the spacecraft flies on an elliptical path in a plane at the same angle to the equator as the latitude of the launch site—in this case, 28.5°.
2. The orbital altitude is then increased to 800 nautical miles by using the Hohmann transfer. This is a minimum energy maneuver where the thrusting is done at the apogee and perigee of the orbit.
3. A plane change is accomplished to permit rendezvous with another spacecraft in a different plane.
4. After rendezvous and docking with the second spacecraft, say, to replenish propellants, our spacecraft undocks and drifts away.
5. The spacecraft then thrusts in a new direction for transplanetary injection. Escape velocity is achieved, and the spacecraft leaves Earth on a hyperbolic trajectory toward the target planet.
6. Along the way, course corrections are made using small velocity increments {delta V’s in space parlance).
7. The spacecraft flies to the target planet or passes nearby and continues out into space. These mission segments are shown pictorially in Fig. 1.
To accomplish the guidance function during each of these mission segments, the GN&C system must have reasonably precise knowledge of the pointing direction of the vehicle and the acceleration during thrusting. Devices used to obtain this information are called inertial sensors and include the gyroscope and accelerometer. Further, for the rendezvous phase, it needs to know the relative position of the spacecraft to the targeted vehicle; rendezvous radar can be used for this purpose. For the docking phase, a near-in distance-measuring sensor, such as a laser, is required.
Gyroscopes. The gyroscope, or gyro as it is usually called, is a spinning wheel supported in rings called gimbals. The gyro has two properties that are useful for guidance applications—the tendency to remain fixed in alignment in space if undisturbed, and the tendency to precess predictably when a torque is applied to the gimbal 90° to the spin axis.
Suppose that a gyro were mounted in a spacecraft. Suppose further that some method is used to spin the wheel and measure angular movement of the gimbals. A gyro used in this manner is termed a vertical gyro. Rotational motion of the spacecraft about all axes except the gyro spin axis could be measured and used for guidance purposes. For the case of spacecraft rotation about the gyro spin axis, a second gyro whose spin axis is at 90° to the spin axis of the first gyro could be added. Some aircraft and missiles that have short flight times use gyros in this manner for attitude control during flight (see, for example, the discussion in Ref. 1). However, drift due to bearing friction and difficulties in precise readout of the gimbal positions usually make this application unsuitable for spacecraft that have precise trajectory requirements and long flight durations. In practical applications for modern spacecraft, the property of precession is more useful.
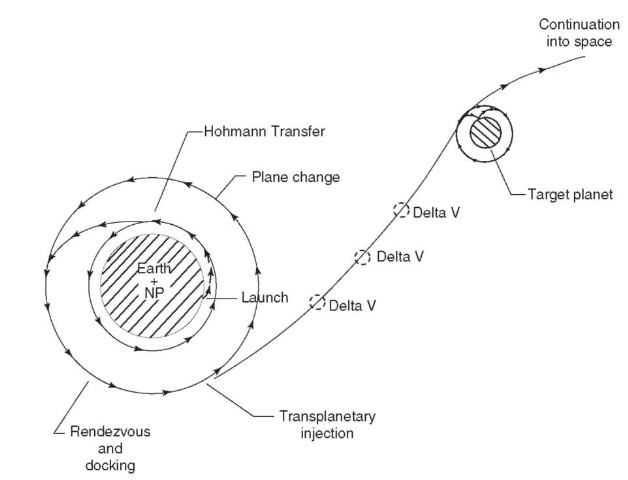
Figure 1. Hypothetical space mission.
The spinning wheel in a gyro has an angular momentum and a rate of precession given, for small disturbances, by the expressions
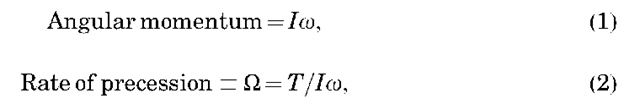
where I is the inertia of the wheel, o is the angular velocity, and T is the torque applied at 90° to the axis of spin.
Suppose that a gyro is mounted in a vehicle, as shown in Fig. 2. In this drawing, the two gimbals on which the spinning wheel is mounted are clearly visible. As the vehicle rotates about the axis labeled input axis transverse to the spin axis, it exerts a torque T on the spin axis and there is precession about the axis labeled output axis. A measure of the rate of precession will be proportional to the vehicle rotation, as shown by Eq. 2. A gyro used in this manner as a rate sensor is called a rate gyro. To keep the displacement of the wheel within narrow limits, a restoring torque motor must be used. Further, if the rate of precession is integrated over time, a value of vehicle angular displacement is determined. A rate gyro used in this manner is termed an integrating rate gyro. This approach to determining vehicular attitude is usually much more accurate than the vertical gyro approach.
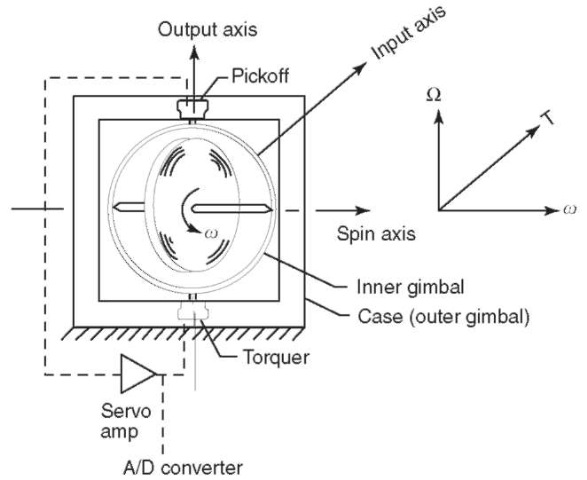
Figure 2. Gyroscopic precession.
When the gyro is used as a sensor, a number of design considerations come into play. First, the wheel is spun using a high-efficiency electric motor. Next, in an effort to reduce volume, the wheel may be made small and the spin rate increased to retain high angular momentum, a desirable feature for measuring very small angular rates. Next, bearings inevitably cause some disturbing torques on the wheel, and in an effort to reduce this effect, the wheel may be supported on a thin film of liquid or gas in lieu of conventional bearings. An optical pickoff is preferable to inductive pickoffs to reduce reactive forces and to measure very small rates. Finally, restoring torque commands may be in the form of pulses that provide a compatible interface with a digital computer. Some design approaches for mechanical gyros used in spacecraft can be found in Ref. 2. Optical Gyros. Another type of sensor for measuring rotational displacement is the so-called ring laser gyro (RLG). This is not a gyro in the conventional sense in that there are no moving parts. The principle of operation is the Sagnac Effect discovered in 1913 (3). The sensing element is a laser beam that is split into two beams directed clockwise and counterclockwise in a somewhat circular, closed, vacuum chamber. Three or more mirrors are arranged in a “ring” around the chamber so that the two beams are reflected back to the source where there is a detector. A conceptual design approach is shown in Fig. 3. If the chamber is rotated in either direction about an axis perpendicular to the plane of the mirrors (i.e., the input axis), there will be a measurable difference (phase shift) in the travel times of the two beams because one will travel a shorter distance than the other. The output of the RLG can be digitized for rotational rate output and then integrated over time for a measure of angular displacement. The disadvantages of RLGs are the difficulty and cost of achieving and maintaining the necessary mechanical alignment (4).
Figure 3. Ring laser gyro.
Fiber-optic gyroscopes (FOG), sometimes called interferometric fiber-optic gyroscopes (IFOG), operate on the same principle as the RLG in that there are two beams of light directed in opposing loops, but in this case the medium is optical fiber. A conceptual drawing of the FOG is shown in Fig. 4. In general, FOGs are easier to fabricate and align than RLGs and are more suitable for microminiaturization. One disadvantage is that scale factors in FOGs are usually nonlinear. Also, the fiber must be carefully chosen to avoid the potential of becoming unserviceable due to aging or radiation in space. FOGs have flown on the Clementine and Technology for Autonomous Operational Survivability (TAOS) spacecraft (4). An extensive discussion of the FOG may be found in (5). Vibratory Gyros. The vibratory gyro is another type of gyro different from the classical mechanical gyro. The ancestry of this type can be traced to the experiments of G. G. Bryan, a British physicist, who studied vibrating wine glasses (6). He discovered that the induced vibrational pattern on a glass would move (precess) if the wine glass were rotated about its stem and that the displacement was proportional to the rotational rate. This is shown in Fig. 5. An example of this type of gyro is the hemispherical resonator gyroscope (HRG) discussed in Ref. 7. In this example, the resonating element that is analogous to the wine glass is a 30-mm diameter bell made of fused silica. A surrounding housing induces vibration and also senses the nodal pattern shift through the use of capacitive pick-offs. This gyro has been used on satellites and on the Jet Propulsion Laboratory’s Cassini spacecraft. The main advantage of the HRG is that there are no moving parts other than the resonator bell. A disadvantage is that the case must be evacuated and vacuum-sealed to prevent air damping.
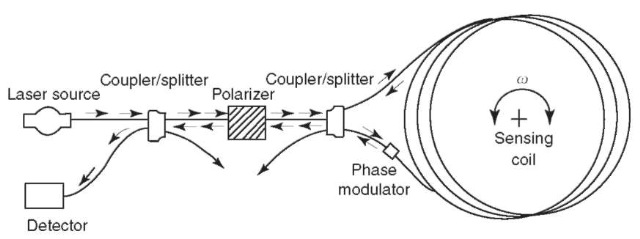
Figure 4. Fiber-optic gyro.
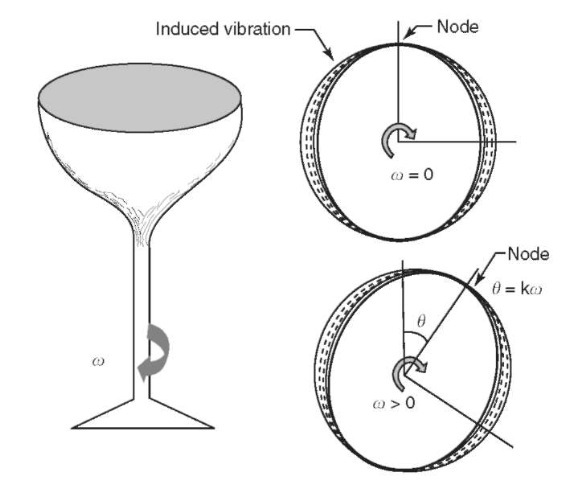
Figure 5. Vibrating bell gyro.
The tuning fork gyro shown in Fig. 6 is another type of vibratory gyro. In this case, the tines are excited in the plane of the tines. As the tuning fork is rotated about an axis parallel to the tines, they tend to continue oscillating in the original plane, as shown in the vector diagram in the figure. The vector component perpendicular to the plane of the tines is proportional to the rotational rate and may be measured by capacitive or optical sensing. Materials used for the tuning fork include crystalline quartz and silicon. Crystalline quartz is a highly stable piezoelectric material suitable for micromachining (8). In the case of silicon, the fork may be part of an integrated circuit chip where the controlling and sensing electronics are designed into the chip (9).
Accelerometers. Accelerometers are devices used to sense changes in velocity. They are made in a number of ways, but the common feature of most is a mass that moves in accordance with Newton’s second law. This sensing mass, sometimes called the proof mass, may be suspended in a number of ways and held in the neutral position by a magnetic field. As the acceleration is sensed by the mass and it begins to move, a pickoff detects the movement and sends a restoring signal through an amplifier to the restoring coil. Rather than hold the mass in a neutral position, some designs force the mass to swing back and forth on a pendulum using a series of back and forth pulses. This restoring circuit also sends the restoring pulses to a counter that adds the positive and negative pulses algebraically; the sum represents the sensed acceleration. If the counter is coupled with a digital computer and integrated over time, it can keep an ongoing status of vehicle velocity. This type of accelerometer, called a pulsed integrating pendulous accelerometer (PIPA), was used successfully in the NASA Apollo Lunar Landing Program (10).
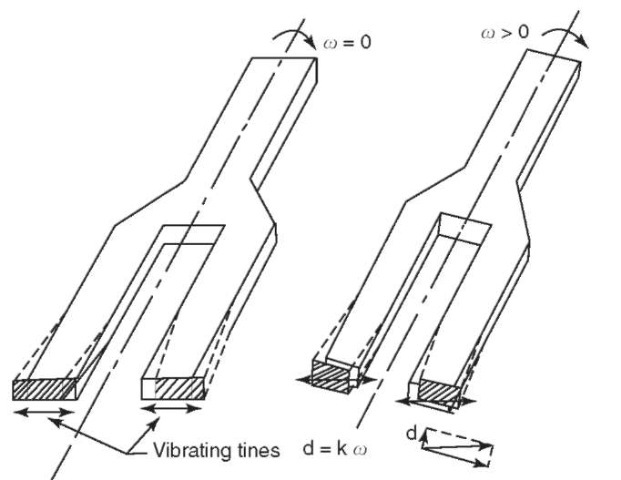
Figure 6. Tuning fork gyro.
Advancements in the past decade in microelectromechanical systems (MEMS), also known as microsystems technology (MST), have produced accel-erometers of continually decreasing size, mass, and power usage (11). Using the same principles of vibratory gyros discussed before, sensing elements now include flexing quartz seismic beams and ”squeezed film.” Movement may be detected by measuring changes in capacitance between the flexing mass and the adjacent fixture. Nanotechnology, generally defined as the next order of size reduction, will no doubt reduce the size of accelerometers further. Inertial Measurement Units. The stable platform, variously referred to as the inertial platform, guidance platform,or inertial measurement unit (IMU) is a common application of gyros and accelerometers. In a typical approach, a group of three single-axis gyros or two dual-axis gyros is mounted on a rigid platform, and their input axes are aligned orthogonally. Three single-axis accelerometers, or two dual-axis accelerometers, are also mounted orthogonally on the platform. The platform is then mounted on two or three gimbals, and the restoring torque signals from the gyros are used to command the gimbal drive motors. The result is that, after initial erection and alignment, the platform is maintained inertially fixed in space. A platform designed in this manner provides an inertial attitude reference and measures accelerations along the inertially fixed axes of the platform. This information can be used by a flight computer to calculate and maintain the status of attitude, acceleration, velocity, and position of the platform.
The GN&C system then essentially flies the platform through space, and the vehicle moves around the platform in the process.
The three-gyro, three-accelerometer platform was used on the NASA Apollo Lunar Landing Program (10). The two-gyro, two-accelerometer IMU is currently used on the NASA Space Shuttle (12). The Space Shuttle IMU is shown in Fig. 7. For a further discussion of IMUs, see Ref. 13.
Stap-Down IMU. The limitations of early onboard flight digital computers encouraged a marriage with gimballed IMUs because of their ability to erect themselves and maintain alignment for at least short times using self-contained torquer motors and dedicated electronics. Even if the flight computer failed, the IMU alignment data could be used in these short periods of time to drive cockpit displays for manual steering. Later on, dedicated local processors within IMUs off-loaded the flight computer even more by applying scale factors, correcting biases, and encoding data words. Over the years, gimballed IMUs have earned a reputation for reliability and have become cheaper to produce.
As onboard digital computers have grown in capability there has been a trend to replace the gimballed IMU by an assembly of gyros and accelerometers rigidly mounted on the spacecraft structure. This approach is called the strap-down IMU or strap-down guidance system. In this approach, the flight computer must do all of the angle resolutions (body angles to inertial angles, or body angles to Euler angles) and continually maintain the inertial reference. Further, corrections must be made by the flight computer (or a dedicated local processor) to eliminate the effects of spacecraft rotation on the accelerometers. Strap-down systems are generally smaller than gimballed IMUs, require less electrical power, and are cheaper to build. A disadvantage is that they must be continually serviced by the flight computer, and if either the strap-down system or the flight computer should fail, inertial reference is instantly lost.
It is interesting to note that the Apollo Program spacecraft used a gimballed platform for the primary system and a limited form of a strap-down IMU for backup. In the latter case, body-mounted gyros were used for backup angular rate and displacement information for both the flight computer for automatic steering and displays for manual steering. But there were no body-mounted accelerometers, and if the gimballed IMU accelerometers failed, thrust duration had to be manually timed.
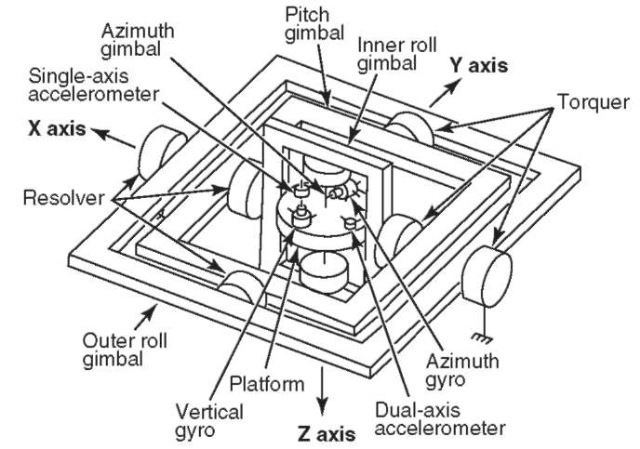
Figure 7. Space Shuttle inertial measurement unit.
It seems likely that future trends in MEMS and nanotechnology will continue to reduce the size and power usage of strap-down IMUs, making them more and more attractive for spacecraft use. However, inherent time-dependent inaccuracies in both types of IMUs require realignment using noninertial sensor or manual updating.
Rendezvous and Docking Sensors. In the hypothetical mission described before, there is a phase when the spacecraft must approach and dock with another spacecraft. Assuming that the target is passive and if the spacecraft is not manned so that manual control may be employed, the maneuver must be accomplished automatically by the onboard GN&C system. Candidate sensors for the rendezvous phase would include a Doppler radar and possibly the Global Positioning System for rendezvous in Earth orbit (14,15). A laser might be suitable for docking. Both translational and rotational commands to the spacecraft attitude control rockets are required and would be generated by the guidance function of the GN&C system. The guidance algorithm must be carefully scripted so that the spacecraft is slowed down enough to prevent impact damage but still has enough kinetic energy on impact to overcome the resistance of the latching mechanism.
Space Navigation
The foundation of space navigation was laid in the seventeenth century by two major advances. Early in the century, Johann Kepler, using the observations of Tycho Brahe, empirically derived his laws of planetary motion. The first law, and the most important for celestial navigation, stated that the planets of the solar system move about the Sun in elliptical orbits and the Sun is at one focus of the ellipses. Later, Sir Isaac Newton stated his laws of motion and formulated the law of universal gravitation. His work confirmed Kepler’s findings and allowed extension to celestial bodies other than planets, for example, comets, and to motions described by conics other than ellipses. These trajectories include circles (a special case of the ellipse), parabolas, and hyperbolas. A discussion of the historical background of this development can be found in Ref. 16. (See also article Earth Orbiting Satellite Theory by S. Nerem in this topic.)
Newton’s law of universal gravitation may be stated generally mathematically as

where F is the magnitude of the force of attraction, m1 and m2 are the masses of the two bodies, s is the distance between them, and G is the gravitational constant whose numerical value depends on the system of units used. The force F points in the same direction as the line s that joins the two masses.
Equation 3 may be applied with reasonable accuracy to a spacecraft orbiting Earth if certain simplifying assumptions are made:
1. Let m1 represent the mass of Earth; Earth is of uniform density and is spherically symmetrical, that is, the oblateness of Earth is ignored. This allows the Earth to be treated as a point mass at its center.
2. Let m2 represent the mass of the spacecraft, so small relative to the mass of Earth that the center of mass of the system lies at the center of Earth.
3. Let m1 be fixed in inertial space with the origin of the reference axes at its center.
4. The spacecraft is in coasting flight with only gravity acting on it, that is, other forces such as aerodynamic drag, solar winds, and electromagnetic forces are ignored.
These assumptions allow simplifying the analysis to what is generally termed the ”restricted two-body problem,” and the approach may be used for spacecraft operating near other relatively large bodies, for example, where m1 represents the Sun, Moon, or one of the planets.
Following the approach of Mueller in Ref. 17, the spacecraft equations of motion can be derived as follows. Using polar coordinates and vector notation, we show the Earth-spacecraft coordinate system in Fig. 8. Referring to Newton’s second law and restating Eq. 3 in vector form in the polar coordinate system,
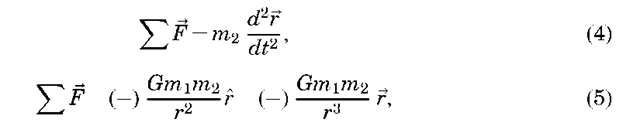
where r is the distance between the masses, r is a unit vector that points along the line joining the two masses.
Combining Eqs. 4 and 5 and simplifying produces

where m is defined as a constant m = Gm\. Equation 6 is the vector differential equation of motion for the restricted two-body problem. Note that it is independent of m2.
Using the methods described elsewhere in this topic (see article Earth Orbiting Satellite Theory by S. Nerem) and referring to Fig. 8, two equations of importance for an orbiting spacecraft can be derived from Eq. 6:
and

where g is defined as the flight path angle.
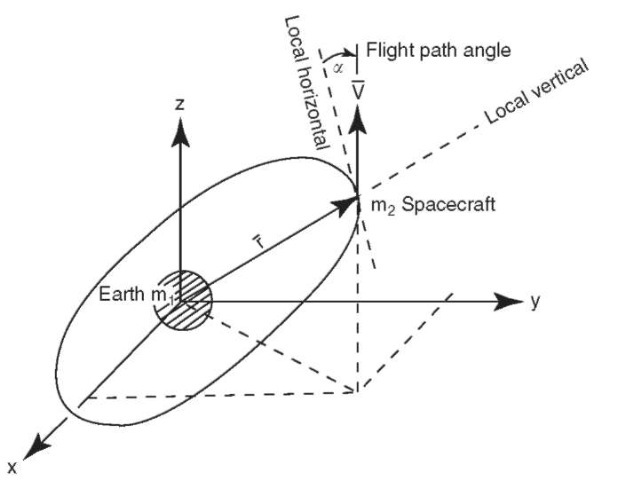
Figure 8. Earth-spacecraft coordinate system.
E is a constant in Eq. 7, termed the specific mechanical energy of the spacecraft, implying a continual exchange of kinetic energy and potential energy throughout the orbit. H in Eq. 8 is called the specific angular momentum and is also constant throughout the orbit. Notice that as r increases, v decreases, as might be expected intuitively.
Finally, referring again to the article by S. Nerem, Eq. 6 can be solved, resulting in the following scalar equation termed the trajectory equation:


r = q-p-• (10)
1+ e cos n

In summary, application of these laws to a spacecraft operating in a central force field results in trajectories that are similar to those of celestial bodies. A coasting spacecraft that has sufficient energy will orbit Earth in a plane and in an elliptical fashion. With the additional thrusting it can be made to travel further out to loop around the Moon and return to Earth, or be captured in an orbit about the Moon. Even more thrusting will cause it to escape Earth’s gravitational pull and proceed on a parabolic or hyperbolic path to one of the other planets or into deep space. The resulting trajectories can be divided into conical segments, whose combinations are called patched conics.
As mentioned earlier, limitations in onboard expendables require planning most space trajectories carefully in advance of the actual flight to achieve the most economical and efficient missions. Launch dates, orbital plane changes, midcourse velocity changes, and rendezvous points must be determined by working backward from a desired target along the way and at the end of the flight. This is usually done by using numerical integration with considerable trial and error adjustments.
Once the mission plan is determined, navigational sightings are defined in terms of times, locations, and types of sensors to be used. At each point, the sightings are made, the information is routed to the onboard flight computer, and the inertial platform is aligned. If an adjustment is required in the state vector of the vehicle, attitude alignments of the vehicle are made and midcourse delta Vs are made using the thrusters on the vehicle. This is repeated as often as required to achieve mission goals.
On the launch pad, the inertial measurement unit is held in a locked position relative to the spacecraft until the last practical moment, usually a few minutes before ignition. In the minutes after IMU release to actual vehicle liftoff, the IMU is controlled by a gyrocompass program to keep it aligned relative to Earth. At liftoff, the IMU is allowed to go inertial and remain so until the next navigational update in flight.
During flight, there are several types of navigational updates. Ground radar tracking is the most common for spacecraft orbiting Earth. Optical sensors may be used to take sightings of Earth, the Sun, or the stars. These sensors include star trackers, horizon scanners, or Sun seekers for automatic navigation. For the manned NASA Apollo Lunar Landing Program, the astronauts made visual sightings using a telescope and sextant that were coupled electronically to the flight computer. All of these sensors are usually carefully mounted on a rigid navigational base that also supports the inertial measurement unit, so that angular resolution from an optical sensor to stable member axes can be made precisely.
Navigational fixes can also be made using the Global Positioning System (GPS) satellites [see also the article on Global Positioning System (GPS) elsewhere in this topic]. This approach can be used to determine the vehicle attitude as well as the location in space if multiple receivers are located precisely on the spacecraft and their relative positions are differentiated (15). Star Trackers. The star tracker is an automatic optical device used to determine the angle between the spacecraft and a luminous body typically outside the solar system. Planets do not make good targets because they lie in a fairly narrow band (the zodiac) and their motion is erratic compared to stars many light-years away. A candidate group of stars is usually preselected and stored in the flight computer along with their general location and their brightness number. The spacecraft is oriented so that the star tracker points in the general direction of a candidate star and then searches until a match is made. Alternately, the tracker itself may be gimballed and allowed to move relative to the spacecraft axes. Two different sightings are enough to establish the spacecraft’s position in space or to align the IMU stable member, but a third or more additional fixes are used for confirmation and greater accuracy. Star trackers now in production have angular accuracy of 0.1 arc seconds or less (18). Star trackers are sometimes used to track other spacecraft, and they may be combined with cameras for photography.
Horizon Scanners. The horizon scanner is used to determine the local vertical of a spacecraft that is orbiting Earth or other planetary bodies. The local vertical may be considered a vector from the center of mass of the vehicle to the center of Earth. Three or more sightings are taken of Earth’s horizon, as shown in Fig. 9, and the angles to the local vertical relative to the spacecraft body axes or inertial axes are computed geometrically by the flight computer. Once the local vertical is determined, star sightings can be made and the latitude and longitude of the vehicle determined. Since visible light is scattered by Earth’s atmosphere, the sensor is usually designed to detect infrared waves that more sharply define Earth’s horizon. Another advantage of infrared is that Earth radiates heat at infrared wavelengths even when the horizon is not in the direct rays of the Sun, and, consequently, sightings can be made on the dark side of Earth.
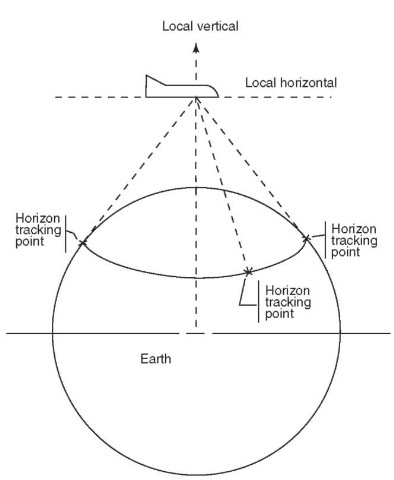
Figure 9. Horizon scanner.
Sun—Earth Sensors. Sun—Earth sensors, sometimes individually referred to as Sun seekers or Earth sensors, are sometimes used as attitude determination devices for spacecraft. They are relatively simple to build, and sightings are usually reliable because the Sun and Earth are large targets and hard to miss. But for the same reasons and because of the relatively rapid movement of Earth in its orbit, they are not usually as accurate for navigation as other devices previously discussed. A principal use of Sun seekers is to orient the vehicle relative to the Sun for thermal control.
Radio Navigational Aids. For Spacecraft required to return safely to Earth and land (e.g., the NASA Space Shuttle Orbiter) or land on other bodies, one or more radio navigational aids may be required. The simplest of these is the radar altimeter, which allows the spacecraft to measure altitude autonomously above the surface of the landing zone. In the Space Shuttle Orbiter, the radar altimeter measures altitude from about 5000 ft down to touchdown.
Tactical Air Navigation (TACAN) units are used on the Space Shuttle Or-biter to determine the slant range and magnetic bearing of the Orbiter during landing approach. This is not an autonomous capability, and several precisely located active ground stations are required. The maximum range of TACAN is about 400 nautical miles. The Orbiter acquires bearings at a range of about 300 nautical miles and 160,000 ft altitude after entry blackout. TACAN data can be used down to an altitude of about 1500 ft.
For final approach, the Orbiter uses the Microwave Scanning Beam Landing System (MSBLS). This system requires active ground stations located immediately adjacent to the runway. The Orbiter acquires the MSBLS signal at a range of 8 to 12 nautical miles and at an altitude of approximately 18,000 feet. The Orbiter Commander usually takes over manually over the runway threshold at about 100 feet altitude.
Information on the NASA Space Shuttle is taken from Ref. 12.
Control
A number of functions must be performed during spacecraft flight that fall under the general heading of control:
• During navigational observations, the spacecraft must be aligned relative to an inertially fixed axis system and the attitude stabilized within a very narrow angular dead band. This is sometimes called the attitude hold mode.
• During periods of thrusting, the spacecraft must be pointed in the correct direction, and the thrust vector controlled. This is usually called the delta V mode.
• Spacecraft attitude hold relative to the Sun may be required, or perhaps the vehicle is slowly rolled (so-called “barbeque” mode) for thermal control.
• Attitude control may be required in conjunction with the deployment of certain mechanisms such as solar panels, radiators, docking mechanisms, and manipulator arms.
• If the spacecraft is to land on Earth or on one of the planets that has an atmosphere, control during atmospheric entry may be required and may necessitate blending of attitude control rockets and aerosurfaces. Landing control is likely to be required and may include control of aerosurfaces, speed brakes, parasails, drag parachutes, landing gear, wheel brakes, and steering on the ground.
* Effector command signals must be processed (scaled, mixed, prioritized, time-delayed) and routed.
Depending on the GN&C system design, attitude change commands may come from the flight computer, directly from the flight crew, or from the ground via radio links. Attitude stabilization commands may come from body-mounted gyros that are generally less accurate than those used for inertial guidance but may serve as emergency backups for the IMU. A newer technique for stabilizing spacecraft in Earth orbit uses differential Global Positioning System (GPS)-de-rived position data from multiple receivers located remotely from each other on the spacecraft. It has been found that attitude knowledge of the order of 0.05° is possible (15). Body-mounted accelerometers may be used for docking sensing or aerodynamic drag sensing during entry.
Effectors. Devices that produce intentional reactive forces on the spacecraft are termed effectors and may include any of the following:
* Attitude control thrusters that use cold gases or reactive chemicals as pro-pellants. These may also be used for small translations for such maneuvers as docking.
* Major engines that produce large changes in the velocity of the spacecraft {delta V). Both thrust level and direction {thrust vector control) may be controlled.
* Reaction wheels where the wheel rotational rate is accelerated or decelerated to achieve reactive torquing of the spacecraft and a corresponding change in attitude.
* Control moment gyros that are typically mechanical gyros torqued electrically so that the resulting precession produces a desired change in spacecraft attitude.
* Aerodynamic surfaces and drag devices.
* Tethers that produce electromagnetic thrusting.
Usually the effectors themselves are not considered part of the GN&C system, but their control electronics are. Analysis of the effects on vehicle motion is usually considered a GN&C responsibility. A simplified generalized block diagram of control function is shown in Fig. 10.
Environmental Disturbances. There are several disturbances that can cause a variation in attitude and possibly tumbling or wobbling. These are usually more noticeable during quiescent periods when the spacecraft is allowed to drift:
* Gravity gradient effects, usually significant when orbiting or flying near a large body.
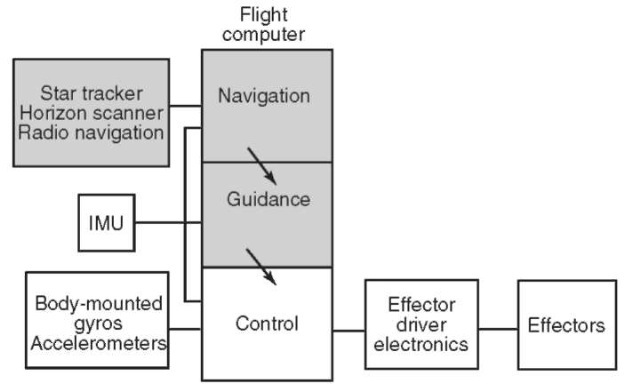
Figure 10. Control block diagram.
* Aerodynamic drag and moments when flying near a body having an atmosphere.
* Solar radiation pressure, usually significant when the spacecraft configuration includes large planar surfaces, such as solar cell panels.
* Electromagnetic induction when flying through the magnetic field of a large body.
The effects of these disturbances are difficult to calculate accurately but may be estimated using the methods of Refs. 19 and 20.1 At the appropriate time, when a fixed attitude is required, these must be counteracted by the attitude control system. Often a small angular dead band is desired and is maintained by use of the reaction wheels, control moment gyros, or attitude control thrusters. In the last case, thruster propellant usage is always a consideration and sometimes leads to sophisticated electronic logic for duty cycle optimization.
Reference Axis System. Since effectors and some sensors are mounted rigidly to the spacecraft structure, it is customary for control analysis to use an axis system originating at the center of mass of the spacecraft. This is depicted in Fig. 11. Symbols are defined in Table 1, followed by a sign convention in Table 2. Equations of Motion. Development of the equations of motion for all mission phases of a spacecraft is an arduous task and beyond the scope of this article. The usual approach to analyzing a particular phase is to make certain simplifying assumptions to reduce the number of mathematical terms significant in that phase. Later on, after achieving a basic understanding of the dynamics, correcting terms may be added for evaluation.
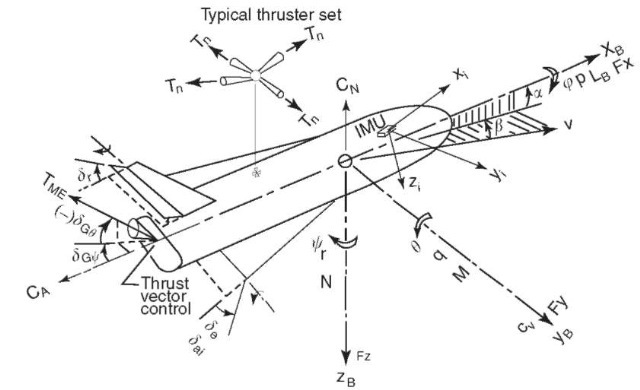
Figure 11. Control reference system.
For example, shown below are six-degree-of-freedom equations of moti for the coasting (in space) attitude hold mode. Simplifying assumptions are follows:
• The spacecraft is considered a rigid body.
• Vehicle mass and inertia remain constant during the period of interest.
Table 1. Body Axes Coordinate System

Table 2. Sign Convention
• The spacecraft is symmetrical about the x-z plane, causing the products of inertia Jyz and Jxy to drop out.
* Terms involving the products of inertia, pJxz and rJxz, are small and may be ignored.

It is helpful to write the equations in this form to get an understanding of the importance of the different terms. Numerical solution on digital computers is usually more convenient after conversion to matrix form. For further discussion on this subject, see Refs. 13, 21-23.
The Flight Computer
There is no part of GN&C technology that has evolved during the past 50 years as dramatically as the onboard digital flight computer. It started in the early 1950s as a fire control computer 4 cubic feet in volume with 250 vacuum tubes (24). Then came the addition of the onboard navigation function with transistor-transistor logic (TTL). Then its use was expanded to include guidance where steering signals were injected into an analog flight control system. By the time of the second-generation Apollo spacecraft, the flight control function was added, integrated electronic circuits were implemented, and the first automatic fly-by-wire flight control was realized. With the Space Shuttle came computer control of all GN&C functions for both atmospheric and spaceflight, computer-driven cockpit displays and computer processing of all manual flight control inputs, and the beginnings of distributed processing. Current flight computers are on the order of cubic inches in volume or smaller, use relatively modest amounts of electrical power, and compute at rates incomprehensible only a few years ago. Microminiaturization is being realized in current applications, and the application of nanotechnology seems likely within a few years.
Today’s flight computer performs an impressive array of functions, depending on the mission of the spacecraft:
* Guidance sensor management and data processing, guidance algorithm computation, and steering signal generation.
* Navigation sensor management and data processing; course evaluation, correction, and forecasting; and trajectory calculation.
* Flight control sensor management and data processing, vehicle attitude control, command mixing and prioritization, effector selection, thrust vector control, attitude thruster control, aerosurface control, vehicle bending and longitudinal oscillation control.
* Aerobraking control, parachute and parasail deployment and steering, nose wheel steering, and wheel braking.
* Systems management for non-GN&C systems, such as electrical power generation, distribution and control; radio/radar/television communications; exploratory payload sensor management and data processing; environmental control systems; and hydraulic and pneumatic systems.
* Consumables accounting and management.
* Flight instrumentation control, data processing, and downlink control.
* Generation of cockpit displays and processing of manual commands for flight control.
* Accommodation of ground commands via radio for software updates, GN&C commands, and data downlinking.
* Redundancy management.
* Vehicle health management (an extension of onboard checkout).
* Multiplex data bus management.
* Distributed processing management.
Input/Output. Probably the most difficult problem in implementing flight computers is communication between the computer and the various devices that are commanded or generate data. The magnitude of this problem can be appreciated intuitively if one imagines the number of wire bundles and connectors required to link the devices to the computer. The problem is compounded if there are redundant computers linked to one another that share the same information. Also, put simply, the digital flight computer is an anomaly in the middle of an analog world, and the necessary conversion of signals from analog-to-digital (A/D) and digital-to-analog (D/A), plus attendant voltage scaling and device scale factor and bias accommodation, is a significant task.
The computer communications problem has been solved successfully in various ways:
• Separating the input/output function and the computation function into two boxes called the input-output processor (IOP) and the central processor unit (CPU). In this approach, the IOP handles the A/D and D/A conversions, voltage scaling, temporary data storage, data bus management (if required), and other functions.
• Doing the A/D and D/A conversion, scale factor adjustment, and voltage scaling at the devices served. In some cases, small local processors are implemented in the devices to perform these relatively simple chores, so that messages to and from the main flight computer are reduced to significant flight data. (This is the beginning of distributed processing.)
• Implementing a multiplex data bus distribution system for communicating with the various devices. In this approach, various devices that have unique addresses are connected to a data bus managed by the IOP. An important advantage of this approach is weight reduction in wiring.
• Sharing the computation task among several processors on the spacecraft. It could be argued that this distributed processing approach is more of a fundamental change in the approach to hardware and software than just a solution to the I/O problem. Certainly, it significantly affects the total software design, implementation, and verification/validation approach. In addition, it usually reflects not just a GN&C decision, but total spacecraft system engineering methodology.
Real-Time Operation. The requirement of uppermost importance for flight computers doing GN&C computations is the ability to keep up with the dynamics of the vehicle and the sensors that provide input data. Whereas batch processing computers in typical ground settings simply run longer when necessary to complete a job, such a delay can be deadly in flight computers in the loop of highly dynamic flight scenarios. The flight computer must maintain system stability, provide computational precision, service sensors, accept interrupts, cope with failures, and even monitor itself while running on control software cycle times typically of 40 milliseconds. The computation bandwidth is almost impossible to estimate accurately early in the design phase of a program, and even the most generous growth margins are usually exceeded and call for compromises to be accommodated later on in the flight software.
A key characteristic of the computer loading is the iterative nature of many calculations, particularly in navigation. There will be errors from a number of sources, including navigation sensor measurements and system mechanization.
A technique for handling these errors is the Kalman filter (25,26), a stochastic analysis and estimation process used extensively in space, aircraft, and missile computers since the early 1960s. Beginning with a priori knowledge of system errors, the Kalman filter continually performs a statistical error analysis and predicts new values for system variables. The resulting product is continuing improvement in position determination.
Flight Software. In the early days of general-purpose digital computers, and especially in digital flight computers, computation times were extremely slow by today’s standards, and random access memory (RAM) was bulky and expensive. The typical computer programmer was a mathematician who likely had a keen appreciation of the overall computation objectives and was driven to code austere programs in what was termed machine language in those days but called assembly language today. Major disadvantages in that software coding approach were that it was labor-intensive and only the original programmer understood the logic behind his organization of the computer program. If other programmers were brought in to modify the program, there was usually some unproductive period to learn the code already in existence. The major advantage was that the assembly code was understandable, at least to the original programmer, and was easily modified. The GN&C engineer often simply had only to speak in general terms to the programmer to have a change incorporated in a timely manner.
Since those early days, three things have happened to cause a revolution in the way flight software is produced today: computation rates have increased by orders of magnitude, random access memory has become inexpensive, and higher order languages (HOL) have become predominant in the development of software programs. Now, software engineers and programmers are formally educated in information systems technology rather than mathematics. The use of higher order languages such as FORTRAN, C, C ++, Ada, and HAL/S makes the flight software engineer and programmer very productive in terms of assembly code generated. And once software engineers or programmers learn the rules and methods for a particular HOL, they can become productive immediately without knowing very much about the ”big picture” of the flight program.
This evolution in computer hardware and software production is not without drawbacks. The very universality of a typical HOL that makes it attractive to modern diverse users also produces very inefficient assembly code. Traditionalists cringe at the squandering of RAM, and even today there never seems to be enough RAM as a spacecraft program progresses. Then, there is the assembly code itself—often virtually indecipherable and difficult to change if relatively simple modifications (called patches) are necessary. The alternative is to make the changes in the source code in the HOL and recompile, a time-consuming process and so prone to introducing undesirable effects that lengthy reverification is usually required. An unfortunate result of this modern approach is that the GN&C engineer usually does not have a thorough knowledge of the flight software program and has difficulty developing an intuitive ”feel” for the program. He must rely almost exclusively on the formal verification/validation of the program for confidence.
Another characteristic of the modern GN&C flight software program is that it seems to ”grow like Topsy” as the spacecraft design matures. This is an unfortunate product of an evangelistic-like effort in the early days of spaceflight, and still today, by enthusiasts to “sell” the digital flight computer by welcoming more and more functions into the software program as a cheap way of implementation. Software accommodation of a feature may appear initially to be a simple and seemingly inexpensive thing to do, but often the penalties in time and expense for the subsequent verification/validation are not anticipated. A vigorous GN&C system engineering program is probably the best solution for this quandary.
The cost of flight computer software is likely to be the most significant item in the GN&C budget and may exceed the cost of the rest of the GN&C system. There are several important factors involved in containing this cost:
• It is critical to document software requirements in as much detail as possible or the computer may be undersized, or the software cost driven to astronomical levels by changes later on, or both.
• The HOL must be chosen carefully while balancing its suitability, maturity, and compilation time with the availability of software engineers and programmers familiar with it.
• The executive program (operating system) must be carefully planned for real-time operation with the attendant issues discussed earlier.
• Application software must be compatible with the devices commanded, and the software engineer-to-device engineer interaction is expensive and sometimes difficult to orchestrate.
• All software must be designed recognizing the time, manpower, and equipment costs associated with the verification process.
• Configuration management is an absolute must for the duration of the spacecraft project.
• The verification and validation approach must be selected. For verification, will flight computers or computer emulators be used? For validation, will a flight computer plus simple simulator be used, or will an ”iron bird” or high-fidelity avionics integration facility plus high-fidelity simulator be used? And will performance of the verification/validation be done (or repeated) by an independent organization (so-called independent verification and validation or IV&V)?
Current Trends. Flight computers continue to grow in capability—faster computational speeds and greater RAM—and are becoming smaller, less power hungry, and cheaper. Choices that were significant a few years ago are not issues anymore. For example, fixed-point versus floating-point arithmetic is now typically decided in favor of floating-point even though floating-point takes more computing time. Word length is now typically 32 bits, and 16-bit machines are passing from the scene. Lasers are being used for communication within the computer in place of copper wire. More and more devices in the GN&C system have embedded digital processors that take care of much of the computer overhead, thus off-loading the central flight computer. Other advancements are discussed under ”Integrated GN&C” following.
Integrated GN&C
Modern spacecraft GN&C systems have their roots in the automatic pilots {autopilots) developed for aircraft in the middle of the last century to relieve pilots on long flights. Rapid advances were made in the 1930s and 1940s, inspired largely by World War II. Initial, relatively crude, vacuum-driven gyros plus vacuum control valves plus hydraulic actuators gave way to electrical sensors plus electronic (vacuum tube) signal processing plus electrical actuators. Throughout this period, the guidance and navigation functions were typically performed by the flight crew and manual commands could be issued to the aircraft directly or via the autopilot control system. Autopilots were the means used to control bombers with steering commands coming from the famous Norden bombsight. Conceptually, then, the guidance and navigation functions were an “overlay” to the autopilot control system.
During the 1950′s to early 1960′s when onboard digital flight computers came on the scene to perform the G&N functions this overlay approach was followed. Flight computers provided steering commands to the vehicle via the analog control system in much the way aircraft crews had done in the past. The analog control system continued to provide three-axis stability and processed the computer-generated steering commands. This design approach was typical of aircraft and guided missiles of the period, and it was followed on the NASA Gemini spacecraft and the early NASA Block I Apollo spacecraft. It is interesting to note that toward the end of this period when manned spacecraft came on the scene mechanical control linkage gave way to electrical communications between the astronaut and effectors and the expression fly-by-wire originated.
In the mid-1960s, as flight computers became more powerful and compact, the entire GN&C calculation function was assigned to them, and analog channels were retained as backup. Outputs were then made directly to the driver amplifiers of the analog control system to command the attitude control thrusters and large engines for changes in translational velocity and thrust vector control during thrusting. This integrated GN&C System became the standard design approach used in guided missiles, satellites, the NASA Apollo lunar mission spacecraft, the NASA Space Shuttle, and is followed today in the International Space Station. This evolution is shown in Fig. 12.
The integrated approach has several advantages. Since the flight computer performs all the GN&C calculations, the computer program (”flight software”) development can be managed more easily. Flight software design changes can be controlled and implemented with less chance of error. System internal redundancy, if desired, can be implemented more efficiently. Overall GN&C electrical power usage is less. Total system volume and mass are reduced.
This is not to say that the integrated GN&C System is necessarily less complex. Likely, it is not. Computer programs become larger, harder for nondeveloper users to understand, and almost impossible to test completely. Training of flight crew and ground support personnel is usually more tedious and lengthy. Preflight testing of the integrated system becomes more involved and expensive because of the fidelity required.
Nonetheless, the integrated GN&C System provides the capability of performing more complex missions and is more flexible for design changes needed for corrections, evolutionary development, and last minute mission changes.

Figure 12. Evolution of the autopilot.
Digital Data Buses. A major advancement in the design of the NASA Space Shuttle was the use of multiplex serial digital data buses for communication with the flight computer. This approach helped solve the computer input/ output loading problem and also provided substantial weight saving. Some 28 data buses are used in the Shuttle design. The data bus is, physically, a twisted shielded pair of wires with transformer couplers for bus protection at each electronic “user” box. The computer uses command and data words that have unique addresses for each receiver so that although all boxes on the bus hear all communications, each responds only to words that have its address. Multiplexers/Demultiplexers convert and format serial digital commands into separate parallel discrete, digital, and analog commands for the various systems served (demultiplexing) and do the reverse for data collected and sent back to the computer (multiplexing). The USAF continued this development, and multiplexed data buses are now common on aircraft, spacecraft, and missiles (27).
An approach similar to the copper data bus discussed before is the fiberoptic bus (28). Fiber has the advantages of potentially higher data rates and less susceptibility to electromagnetic interference or intentional jamming. Disadvantages include larger minimum bend radius for installation and the potential to become unserviceable due to age or environmental effects.
Fiber optics is also considered part of a general class of communications called photonics. This is a term used for the general case in which the medium is light rather than electron flow. In GN&C, the expression fly-by-light is sometimes used. When direct line of sight exists between devices, the use of laser beams or infrared beams for data transfer is possible.
Fly-by-Wireless?. A promising development that could be used in lieu of the data bus is digital spread-spectrum radio frequency communication between the flight computer and devices in the GN&C system. Spread-spectrum is a technique used to reduce or avoid interference by taking advantage of a statistical means to send a signal between two points using different frequencies at different times. The theory is that noise tends to occur at different frequencies at different times. Therefore, even though part of a transmission might be lost due to interference, enough of the message will come through to create noticeably better output compared to fixed-frequency systems. Further, using error correction techniques, the original message can be totally restored. The promise of this approach for aircraft and spacecraft is reduction in size, weight, and power of GN&C systems while offering immunity to natural interference or jamming from man-made equipment.
INVOCON, based in Conroe, Texas, has had considerable success in developing instrumentation for the NASA Space Shuttle Orbiter and the International Space Station by linking sensors to a central controller/transponder via spread-spectrum radio. Using the same principle on a project sponsored by NASA Dry-den Flight Research Center, INVOCON successfully replaced a data bus link from the flight computer to an elevon actuator on a NASA F-18 research airplane (29). This concept is shown in Fig. 13.
Redundancy. The use of backup hardware in aircraft and spacecraft to allow operation in the event offailure dates back many years. In manned vehicles, the crew normally has had the capability to choose the backup, usually degraded in performance, but may have been incapable of making the decision in dynamic situations.
The NASA Space Shuttle, which had a design requirement to remain fully operational with one failure and to remain safe after two failures, probably reached the maximum in complexity in the approach to automatic and manual redundancy management. Basic to the design approach is the provision of four redundant primary flight computers to handle two computer hardware failures automatically and a fifth identical backup flight computer loaded with dissimilar software to be chosen in a manual switchover in case of a generic software error in the primary set. Three or more redundant channels of sensors are shared by all computers, which then command four parallel redundant channels to the effector servoelectronics. The primary flight computers automatically compare and vote by ”majority rule.” In addition, the aerosurface actuators, which have four channels at the secondary (pilot spool) stage, were designed to vote effectively by force fight, that is, three channels overcome the offending fourth channel by force summing three against one. A comprehensive discussion of these features can be found in Ref. 30.

Figure 13. Fly-by-wireless concept.
The requirement of redundancy and automatic redundancy management in spacecraft depends on the need for vehicle survivability weighed against the cost of redundancy implementation. For expendable vehicles, it may be cheaper simply to build more spacecraft than to make them internally redundant. In manned spacecraft, loss of life is so intolerable in this country that safety must be maintained, regardless of cost.
Simulation
The sheer quantity of “black boxes” in a modern day GN&C system begs the question as to whether system end-to-end mathematical analysis is possible. Further, the time-varying, cascading signal flow from the multiple sensors to the flight computer to the various driver electronics for the motion effectors makes end-to-end analysis and solutions by conventional closed form methods virtually unachievable. Moreover, if the solution were tractable for a particular time and set of physical conditions and produced acceptable results from an operational point of view, the flight conditions could change in the next few moments, and the analysis would have to be repeated. The analytical approach commonly used in these situations is known as computer simulation, or simply simulation, where time is the primary independent variable.
Simulations are used in the conceptual design phase of a program and grow in complexity and fidelity as the program matures. Mathematical models of the functions of the different pieces of hardware evolve in complexity from simple first-order equations to higher and higher levels of fidelity. Desktop computers are adequate in the early phases to define and analyze single sensors, signal amplifiers, effectors, and units as complex as inertial platforms. As the program progresses, multiple hardware units are combined, vehicle characteristics and operational environments become better known in more detail, and the simulations are forced to move to larger complexes of computers, data library devices, and resultant data readout devices.
Additional complexity accompanies increased fidelity when the simulation is required to operate in a real-time mode. Real time means that a series of events simulated is calculated on the simulator in the same period of time as the real events would occur. Real-time simulation is used any time there is flight crew involvement or flight-like hardware is substituted for simulated hardware. For GN&C system-level simulations, the flight computer is usually one of the earliest units substituted for its modeled counterpart.
If the flight vehicle is a manned spacecraft, a crew station (cockpit) is usually added. Active crew displays and controls, either flight-like or simulated, are added to allow realistic crew participation for evaluating the GN&C system. If visual cues are required for this crew participation, ”out-the-window” scenes may be included. The NASA Johnson Space Center Engineering Simulator that has some two million lines of computer code is an example of these large man-in-the-loop simulations.
As the program matures, a simulator especially designed for flight crew and ground operations personnel training is usually constructed. This simulator-trainer typically has the highest fidelity of all simulations in the program. All onboard displays and controls are included, and system simulated failures may be introduced to enhance training. For manned spacecraft, out-the-window scenes are included for all phases of the intended vehicle mission, including prelaunch, launch, orbit transfers, midcourse deltaVs, rendezvous and docking with another spacecraft, deorbit, and landing.
Vital to the fidelity of simulations throughout a program are valid mathematical models for the components of the GN&C system, for effectors and other non-GN&C equipment, and for the environment in which the vehicle is supposed to be operating. Simple first-order equations are quite satisfactory early in the design phase, but as actual hardware is built, the fidelity desired increases, and the corresponding mathematical models become more complex. Similarly, equations of motion, environmental models for ambient physical conditions, aerodynamic data, ephemerides, and out-the-window scenes all become more intricate in the drive for fidelity as the program progresses and the design matures. This often results in large simulation complexes that are expensive to create and maintain, but they are indispensable for system development, anomaly investigations, and crew training.
Integration and Verification
The term integration is an overworked word in the aerospace business, but it is quite descriptive in GN&C systems development. Hardware piece parts and modules are integrated (assembled) into line replaceable units (LRUs) or “black boxes”2 that are replaceable as the first level of maintenance on spacecraft. The LRUs are then integrated (combined) to form the whole GN&C system. A similar process is followed in developing flight computer software. As this process is followed, engineering tests are conducted, and design errors are uncovered and corrected. This successive integration is part of the development process and is the most demanding part of GN&C engineering.
Verification is the process of formal evaluation of the hardware and software and is done somewhat in parallel with the integration process. Four methods are generally used and are listed here in order of preference: test, inspection, demonstration, and analysis. These are defined as follows:
Test—the stimulation of the hardware and software under prescribed conditions and the responses measured and evaluated against specifications.
Inspection—the visual examination of hardware, usually in static situations.
Demonstration—operation in a test-like environment but where responses usually cannot be measured and performance must be evaluated subjectively.
Analysis—mathematical and logical evaluation using mathematical models, drawings, flow charts, and photographs.
Formal hardware verification testing begins with the acceptance test at the GN&C system vendor’s plant. This test is conducted before the buyer accepts delivery to ensure that the equipment is functioning in accordance with the requirements of the contract between the vendor and the buyer.
Ideally, one or more LRUs are randomly selected from those already accepted for a subsequent qualification test. The qualification test is conducted at extremes in ambient conditions [pressure, temperature, vibration, input electrical power, electromagnetic interference (EMI), etc.] beyond the limits expected in normal operation. This test ensures that the hardware has comfortable operating margins.
The next level of testing is the integrated system test. In this test, the entire GN&C system is assembled in a flight-like configuration, and stimuli at the sensors are processed through the system to the outputs of the effector driver electronics. This is also sometimes called a system end-to-end test. Debate continues as to whether this test is an engineering development test or a formal verification test, but in reality it is usually both. Certainly, any design errors or generic manufacturing errors that are uncovered must be corrected. A critical part of this exercise is the testing of interfaces with non-GN&C equipment. The importance of this aspect is discussed in Ref. 31.
The final ground verification test is the mission verification test. The significant addition to the integrated system test configuration is a real-time simulation computer complex. This is used to ”close the loop” (i.e., close the flight control loop using simulated vehicle dynamics) and to model missing flight hardware and the vehicle flight environment so that the entire mission, or significant portions, may be “flown” as realistically as practical short of actual flight. Flight computer software is used in the flight computer and is validated in the process. Successful completion of the mission verification test allows certification for flight. This sequence is shown pictorially in Fig. 14.
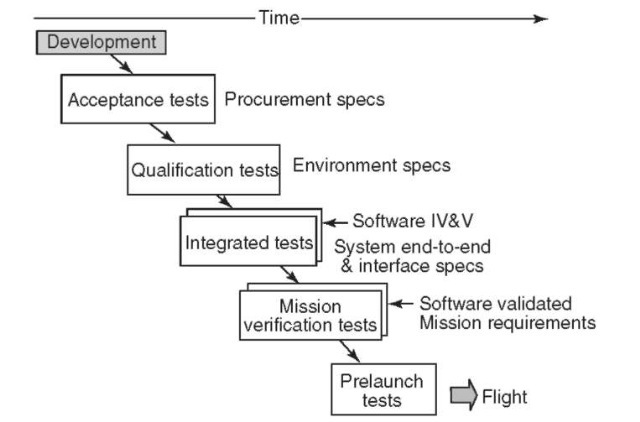
Figure 14. Integration and verification sequence.
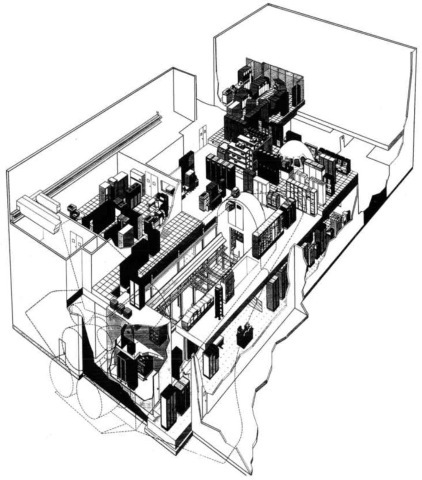
Figure 15. Shuttle Avionics Integration Laboratory
One of the most sophisticated facilities for the integrated system test and the mission verification test is the Shuttle Avionics Integration Laboratory at the NASA Johnson Space Center. An artist’s rendering of the facility is shown in Fig. 15. The avionics are installed in a high-fidelity, three-dimensional full-scale arrangement with flight-like vehicle wire harnesses. The outline of the Orbiter is shown in dashed lines for orientation.
For manned spacecraft, one or more flight tests are usually required before the vehicle, including the GN&C system, is certified for normal operational use.
