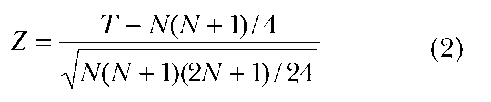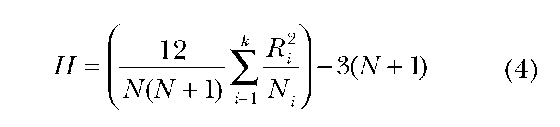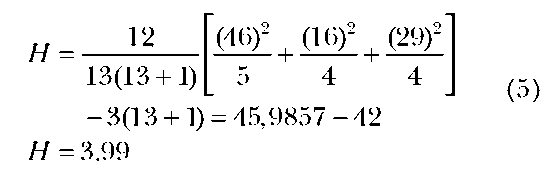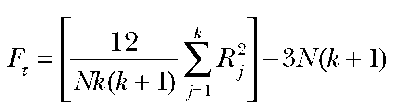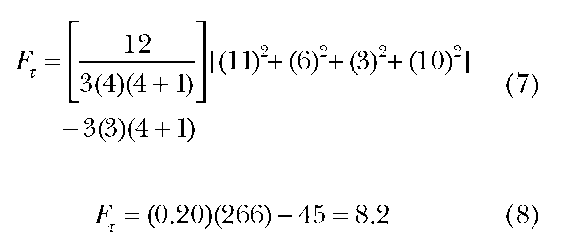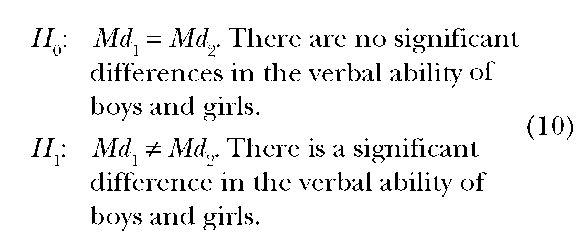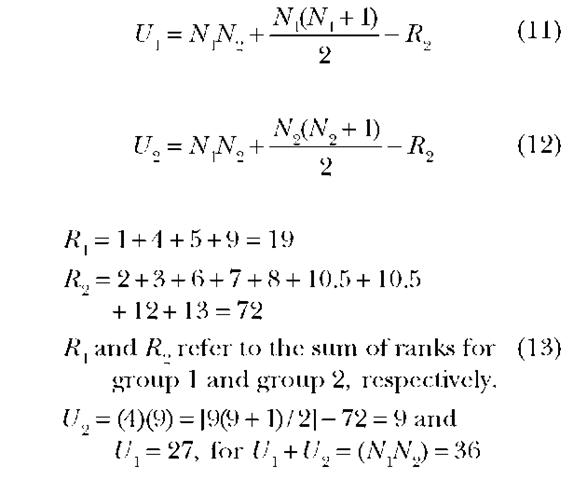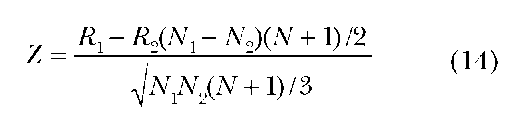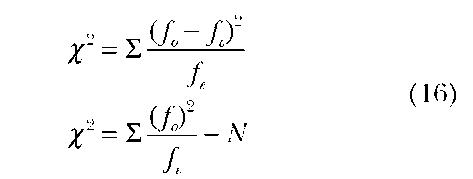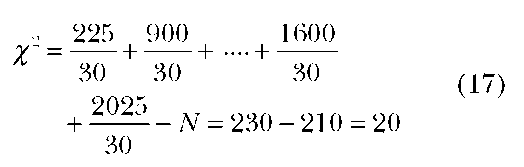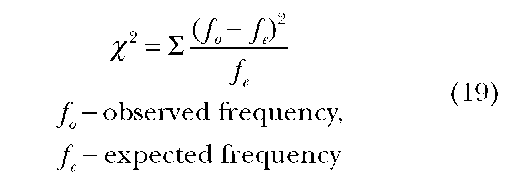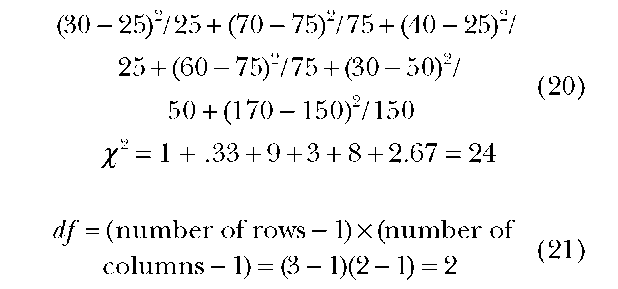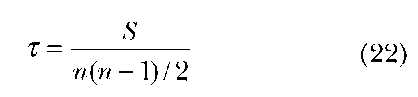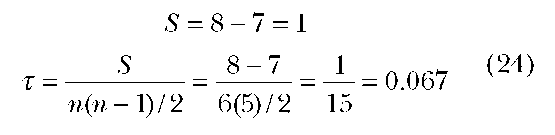Parameters are characteristics of the population being studied such as a mean (|), standard deviation (a) or median (Md). Statistics describe characteristics of a sample. Sample mean (x) and sample median (m) are two examples. In traditional or classical parametric statistics, making inferences from a sample or samples to a population or populations necessitates assumptions about the nature of the population distribution such as a normal population distribution.
Nonparametric statistics may be defined as statistical methods that contribute valid testing and estimation procedures under less stringent assumptions than the classical parametric statistics. However, there is no general agreement in the literature regarding the exact specification of the term ”nonparametric statistics.” In the past, nonparametric statistics and the term ”distribution-free methods” were commonly used interchangeably in the literature, although they have different implications. Nonparametric statistics were often referred to as distribution-free statistics because they are not based on a particular type of a distribution in the population such as a normal distribution. It is, however, generally agreed that nonparametric statistics require fewer, or less stringent, assumptions about the nature of the population distribution being studied, compared to classical parametric statistics. It is important to note that nonparametric statistics are not totally assumption-free either, since they must be based on some assumptions applicable to specific tests, such as lack of ties or the independence of two random samples included in the study. They are flexible in their use and are generally quite robust. Nonparametric statistics allow researchers to arrive at conclusions based on exact probability values and the confidence interval.
The major advantages of nonparametric statistics compared to parametric statistics are that: (1) they can be applied to a large number of situations; (2) they can be more easily understood intuitively; (3) they can be used with smaller sample sizes; (4) they can be used with more types of data; (5) they need fewer or less stringent assumptions about the nature of the population distribution; (6) they are generally more robust and not often seriously affected by extreme values in data such as outliers; (7) they have, in many cases, a high level of asymptotic relative efficiency compared to the classical parametric tests; (8) the introduction of jackknife, bootstrap, and other resampling techniques has increased their range of applicability; and (9) they provide a number of supplemental or alternative tests and techniques to currently existing parametric tests.
Many critics of nonparametric tests have pointed out some major drawbacks of the tests: (1) they are usually neither as powerful nor as efficient as the parametric tests; (2) they are not as precise or as accurate as parametric tests in many cases (e.g., ranking tests with a large number of ties); (3) they might lead to erroneous decisions about rejecting or not rejecting the null hypothesis because of lack of precision in the test; (4) many of these tests utilize data inadequately in the analysis because they transform observed values into ranks and groups; and (5) the sampling distribution and distribution tables for nonparametric statistics are too numerous, are often cumbersome, and are limited to small sample sizes. The critics also claim that new parametric techniques and the availability of computers have reduced the need to use nonparametric statistics. Given these advantages and disadvantages, how does one choose between parametric and nonparametric tests?
Many criteria are available for this purpose. Statistical results are expected to be unbiased, consistent, or robust, or to have a combination of these characteristics. If both tests under consideration are applicable and appropriate, what other criteria may be used in the choice of a preferred test? The power and efficiency of a test are very widely used in comparing parametric and nonparametric tests.
The power of a test is the probability of rejecting the null hypothesis H0 when it is false. It is defined as 1 – B, where B is the probability of a Type II error, or acceptance of a false null hypothesis. If test A and test B would have the same alpha level of significance and the same sample sizes, and test B has a higher power, then test B is considered a preferred choice. However, calculations of the power of a test are often cumbersome. Another way of addressing the issue of the power of a test is through an asymptotic relative efficiency measure. The relative efficiency of a test in comparison to another test is the ratio of the sample size needed to achieve the same power with similar assumptions about significance levels and population distribution. Asymptotic relative efficiency of a test (sometimes called Pitman efficiency) is measured without a limit on the increase in sample size of that test. Thus, for example, when an asymptotic efficiency of Kendall’s T relative to Personian r is given as .912, it means that the T with a sample size of 1000 is as efficient as an r with a sample size of 912. The test for asymptotic relative efficiency is now routinely used in the literature to compare two tests.
Based on these criteria, it can be generalized that nonparametric tests and techniques tend to be preferred when: (1) nominal or ordinal data are involved; (2) robust tests are needed because of outliers in the data; (3) probability distribution or density function of the data is unknown or cannot be assumed, as in the case of small sample sizes; (4) the effects of violations of specific test assumptions are unknown, or only weak assumptions can be made; (5) analogous parametric tests are not available, as in the case of runs tests and goodness-of-fit tests; and (6) preliminary trials, supplemental or alternative techniques for parametric techniques are needed.
NONPARAMETRIC STATISTICAL LITERATURE
The term nonparametric statistics was introduced in the statistical literature in the 1940s (Noether 1984). The historical roots of nonparametric statistics are supposed to go as far back as 1710 when John Arbuthnot did a study that included the proportion of male births in London (Daniel 1990; Hettmansperger 1984) using a sign test which is a nonparametric procedure. Spearman’s rank correlation coefficient, which is widely used even today, was the forerunner of the chi-square test, which was introduced in 1900.
Initial major developments in the field that introduced and popularized the study of nonparametric methods appeared in the late 1940s and early 1950s, though a few nonparametric tests were published in the late 1920s such as the Fisher-Pitman test, Kendall’s coefficient of concordance, and Hotelling and Pabst’s paper on rank correlation in the 1930s. Contributions by Wilcoxon and Mann-Whitney were introduced during the 1940s. The term nonparametric reportedly appeared for the first time in 1942 in a paper by Wolfowitz (Noether 1984). The 1956 publication of Siegel’s text on nonparametric statistics popularized the subject to such an extent that the text was one of the most widely cited textbooks in the field of statistics for a few years. It was during this time that computer software for nonparametric tests was introduced.
The major emphasis in the 1960s and 1970s was on the extension of the field into regression analysis, and analysis of variance to develop tests analogous to the classical parametric tests. It was also discovered during this period that nonparametric tests were more robust and more efficient than previously expected. The basis for the asymptotic distribution theory was developed during this time period.
A number of texts have been published recently (see, e.g., Conover 1999; Daniel 1990; Hollander and Wolfe 1999; Krauth 1988; Neave and Worthington 1988; Siegel and Castellan 1988; Sprent 1989). Some of these texts can be used without an extensive statistical background; they have excellent bibliographies and provide adequate examples of assumptions, applications, scope, and limitations of the field of nonparametric statistics.
The literature on nonparametric statistics is extensive. The bibliography published in 1962 by Savage had approximately 3,000 entries. More recent bibliographies have made substantial additions to that list.
TESTS AND TECHNIQUES
Nonparametric statistics may be divided into three major categories: (1) noninferential statistical measures; (2) inferential estimation techniques for point and interval estimation of parametric values of the population; and (3) hypothesis testing, which is considered the primary purpose of nonparametric statistics. (Estimation techniques included in the category above are often used as a first step in hypothesis testing.) These three categories include different types of problems dealing with location, dispersion, goodness-of fit, association, runs and randomness, regression, trends, and proportions. They are presented in Table 1 and illustrated briefly in the text.
Table 1, which includes a short list of some commonly used nonparametric statistical methods and techniques, is illustrative in nature. It is not intended to be an exhaustive list. The literature literally consists of scores of nonparametric tests. More exhaustive tables are available in the literature (e.g., Hollander and Wolfe 1999). The six columns in the table describe the nature of the sample, and the eight categories of rows identify the major types of problems addressed in nonparametric statistics. Types of data used in nonparametric tests are not included in the table, though references to levels of data are made in the text. Tables that relate tests to different types of data levels are presented in some texts (e.g., Conover 1999). A different type of table provided by Bradley (1968) identifies the family to which the nonparametric derivations belong.
The first column in Table 1 consists of tests involving a single sample. The statistics in this category include both inferential and descriptive measurements. They would be used to decide whether a particular sample could have been drawn from a presumed population, or to calculate estimates, or to test the null hypothesis. The next column is for two independent samples. The independent samples may be randomly drawn from two populations, or randomly assigned to two treatments. In the case of two related samples, the statistical tests are intended to examine whether both samples are drawn from the same (or identical) populations. The case of k (three or more) independent samples and k related samples are extensions of the two sample cases.
The eight categories in the table identify the main focus of problems in nonparametric statistics and are briefly described later. Only selected tests and techniques are listed in table 1. Log linear analyses are not included in this table, although they deal with proportions and meet some criteria for nonparametric tests. The argument against their inclusion is that they are rather highly developed specialized techniques with some very specific properties.
It may be noted that: (1) many tests cross over into different types of problems (e.g. the chi-square test is included in three types of problems); (2) the same probability distribution may be used for a variety of tests (e.g., in addition to association, proportion, and goodness-of-fit, the chi-square approximation may also be used in Friedman’s two-way analysis of variance and Kruskal-Wallis test); (3) many of the tests listed in the table are extensions or modifications of other tests (e.g., the original median test was later extended to three or more independent samples; e.g., the Jonckheere test); (4) the general assumptions and procedures that underlie some of these tests have been extended beyond their original scope (e.g. Hajek’s extension of the Kolmogorov-Smirnov test to regression analysis and extension of the two-sample Wilcoxon test for testing the parallelism between two linear regression slopes); (5) many of these tests have corresponding techniques of confidence interval estimates, only a few of which are listed in Table 1; (6) many tests have other equivalent or alternative tests (e.g., when only two samples are used, the Kruskal-Wallis test is equivalent to the Mann-Whitney test); (7) sometimes similar tests are lumped together in spite of differences as in the case of the Mann-Whitney-Wilcoxon test or the Ansari-Bradley type tests or multiple comparison tests; (8) some tests can be used with one or more samples in which case the tests are listed in one or more categories, depending on common usage; (9) most of these tests have analogous parametric tests; and (10) a very large majority of nonparametric tests and techniques are not included in the table.
Table 1:Selected Nonparametric Tests and Techniques
|
|
|
TYPE OF DATA |
|
|
|
|
|
|
|
Two Related, |
|
|
|
|
|
Two |
Paired, or |
k |
k |
|
Type of |
|
Independent |
Matched |
Independent |
Related |
|
Problem |
One Sample |
Samples |
Samples |
Samples |
Samples |
|
Location |
Sign test |
Mann-Whitney- |
Sign test |
Extension of |
Extension of |
|
\ |
\ |
Wilcoxon rank- |
|
Brown-Mood |
Brown-Mood |
|
|
Wilcoxon |
sum test |
Wilcoxon matched- |
median test |
median test |
|
|
signed ranks |
|
pairs signed |
|
|
|
|
test |
Permutation test |
rank test |
Kruskal-Wallis |
Kruskal-Wallis |
|
|
|
|
|
one-way analysis |
one-way analysis |
|
|
|
Fisher tests |
Confidence |
of variance test |
of variance test |
|
|
|
|
interval based |
|
|
|
|
|
Fisher-Pitman test |
on sign test |
Jonckheer test |
Jonckheer test |
|
|
|
|
|
for ordered |
for ordered |
|
|
|
Terry Hoeffding |
Confidence |
alternatives |
alternatives |
|
|
|
and van der |
interval based |
|
|
|
|
|
Waerden/normal |
on the Wilcoxon |
Multiple |
Multiple |
|
|
|
scores tests |
matched-pairs |
comparisons |
comparisons |
|
|
|
|
signed-ranks test |
|
|
|
|
|
Tukey’s confidence |
|
|
|
|
|
|
interval |
|
|
Friedman two-way |
|
|
|
|
|
|
analysis of |
|
|
|
|
|
|
variance |
|
Dispersion |
|
Siegel-Tukey test |
|
|
|
|
(Scale |
|
|
|
|
|
|
Problems) |
|
Moses’s ranklike tests |
|
|
|
|
|
|
Normal scores tests |
|
|
|
|
|
|
Test of the Freund, |
|
|
|
|
|
|
Ansari-Bradley, |
|
|
|
|
|
|
David, or Barton type |
|
|
|
|
Goodness-of-fit |
Chi-square |
Chi-square test |
|
Chi-square test |
|
|
|
goodness-of-fit |
|
|
|
|
|
|
|
Kolmogorov- |
|
Kolmogorov- |
|
|
|
Kolmogorov- |
Smirnov test |
|
Smirnov test |
|
|
|
Smirnov test |
|
|
|
|
|
|
Lilliefors test |
|
|
|
|
|
Association |
Spearman’s |
Chi-square test of |
Spearman rank |
Chi-square test of |
Kendall’s coefficient |
|
|
rank correlation |
independence |
correlation |
independence |
of concordance |
|
|
|
|
coefficient |
|
|
|
|
Kendall’s taua |
|
|
Kendall’s Partial |
|
|
|
taub tauc |
|
Kendall’s taua |
rank correlations |
|
|
taub tauc |
|||||
|
|
Olmstead-Tukey |
|
Kendall’s coefficient |
|
|
|
|
test |
|
Olmstead-Tukey |
of agreement |
|
|
|
|
|
corner test |
|
|
|
|
Phi coefficient |
|
|
Kendall’s coefficient |
|
|
|
|
|
|
of concordance |
|
|
|
Yule coefficient |
|
|
|
|
|
|
Goodman-Kruskal |
|
|
|
|
|
|
coefficients |
|
|
|
|
|
|
Cramer’s statistic |
|
|
|
|
|
|
Point biserial |
|
|
|
|
|
|
coefficient |
|
\ |
|
|
Selected Nonparametric Tests and Techniques
|
|
TYPE OF DATA |
|
||
|
Type of Problem |
One Sample |
Two Independent Samples |
Two Related, Paired, or Matched Samples |
k k Independent Related Samples Samples |
|
Runs and Randomness |
Runs test Runs above and below the median Runs up-and-down test |
Wald-Wolfowitz runs test |
|
|
|
Regression |
|
Hollander and Wolfe test for parallelism Confidence interval for difference between two slopes |
|
Brown-Mood test |
|
Trends and Changes |
Cox-Stuart test Kendall’s tau Spearman’s rank correlation coefficent McNemar change test Runs up-and-down test |
|
McNemar Change test |
|
|
Proportion and Ratios |
Binomial test |
Fisher’s exact test Chi-square test of homogeneity |
|
Chi-square test Cochran’s Q test of test homogeneity |
Only a few of the commonly used tests and techniques are selected from Table 1 for illustrative purposes in the sections below. The assumptions listed for the tests are not meant to be exhaustive, and hypothetical data are used in order to simplify the computational examples. Discussions about the strengths and weaknesses of these tests is also omitted. Most of the illustrations are either two-tailed or two-sided hypotheses at the 0.05 level. Tables of critical values for the tests illustrated here are included in most statistical texts. Modified formulas for ties are not emphasized, nor are measures of estimates illustrated. Generally, only simplified formulas are presented. A very brief description of the eight major categories of problems follows.
Location. Making inferences about location of parameters has been a major concern in the field of statistics. In addition to the mean, which is a parameter of great importance in the field of inferential statistics, the median is a parameter of great importance in nonparametric statistics because of its robustness. The robust quality of the median can be easily ascertained. If the values in a sample of five observations are 5, 7, 9, 11, 13, both the mean and the median are 9. If two observations are added to the sample, 1 and 94 (an outlier), the median is still 9, but the mean is changed to 20. Typical location problems include estimating the median, determining confidence intervals for the median, and testing whether two samples have equal medians.
Sign Test This is the earliest known nonparametric test used. It is also one of the easiest to understand intuitively because the test statistic is based on the number of positive or negative differences or signs from the hypothesized median. A binomial probability test can be applied to a sign test because of the dichotomous nature of outcomes that are specified by a plus (+) which indicates a difference in one direction or a minus (-) sign which indicates a difference in another direction. Observations with no change or no difference are eliminated from the analysis. The sign test may be a one-tailed or a two-tailed test. A sign test may be used whenever a t-test is inappropriate because the actual values may be missing or not known, but the direction of change can be determined, as in the case of a therapist who believes that her client is improving. The sign test only uses the direction of change and not the magnitude of differences in the data.
Wilcoxon Matched-Pairs Signed-Rank Test The sign test analysis includes only the positive or negative direction of difference between two measures; the Wilcoxon matched-pairs signed-rank test will also take into account the magnitude of differences in ordering the data.
Example: A matched sample of students in a school were enrolled in diving classes with different training techniques. Is there a difference? The scores are listed in Table 2.
Illustrative Assumptions: (1) The random sample data consist of pairs; (2) the differences in pair values have an ordered metric or interval scale, are continuous, and independent of one another; and (3) the distribution of differences is symmetric.
Hypotheses: A two-sided test is used in this example.
H0: Sum of positive ranks = sum of negative ranks in population
H: Sum of positive ranks ^ sum of negative ranks in population
Test statistic or procedures: The differences between the pairs of observations are obtained and ranked by magnitude. T is the smaller of the sum of ranks with positive or negative signs. Ties may be either eliminated or the average value of the ranks assigned to them. The decision is based on the value of T for a specified N. Z can be used as an approximation even with a small N except in cases with a relatively large number of ties. The formula for Z may be substituted when N > 25.
This formula is not applicable to the data in Table 2 because the N is < 25 and the calculations in Table 2 will be used in deciding whether to reject or fail to reject (”accept”) the null hypothesis. In this example in Table 2, the N is 7 and the value of the smaller T is 9.5.
Decision: The researchers fail to reject the null hypothesis (or ”accept” the null hypothesis) of no difference between the two groups, with an N of 7 at the 0.05 level, for a two-sided test, concluding that there is no statistically significant difference in the two types of training at the 0.05 level.
Efficiency: The asymptomatic related efficiency of the test varies around 95 percent, based on the sample sizes.
Table 2 :Total Scores for Five Diving Trials
|
Pairs |
X Team A |
Y Team B |
Y – X Differences |
Signed Rank of Differences T+ |
Negative Ranks T- |
|
1 |
37 |
35 |
-2 |
-1 |
1 |
|
2 |
39 |
46 |
7 |
+4 |
|
|
3 |
32 |
24 |
-8 |
-5.5 |
5.5 |
|
4 |
21 |
34 |
13 |
+7 |
|
|
5 |
20 |
28 |
8 |
+5.5 |
|
|
6 |
9 |
12 |
3 |
+2 |
|
|
7 |
14 |
9 |
-5 |
-3 |
3 |
|
|
|
|
|
T+ = 18.5, T_ = 9.5 |
9.5 |
Related parametric test: The t-test for matched pairs.
Analogous nonparametric tests: Sign test; randomization test for matched pairs; Walsh test for pairs.
Kruskal-Wallis One-Way Analysis of Variance Test This is a location measure with three or more independent samples. It is a one-way analysis of variance that utilizes ranking procedures.
Example: The weight loss in kilograms for 13 randomly assigned patients to one of the three diet programs is listed in Table 3 along with the rankings. Is there a significant difference in the sample medians?
Illustrative Assumptions: (1) Ordinal data; (2) three or more random samples; and (3) independent observations.
Hypotheses: A two-sided test without ties is used in this example.
H0 : Md1 = Md2 = Md3. The populations have the same median values.
H1: Md1 ^ Md2 ^ Md3 All the populations do not have the same median value.
Test statistics or procedures: The procedure is to rank the values and compute the sums of those ranks for each group and calculate the H statistic. The formula for H is as follows:
where N1 = the case in the i th category of rank sums R; = the sum of ranks in the i th sample.
Decision: Do not reject the null hypothesis, as the chi-square value for 2 df at the 0.05 level is 5.99 and the H value of 3.99 is less than the critical value.
Efficiency: Asymptotic relative efficiency of Kruskal-Wallis test to F test is 0.955 if the population is normally distributed.
Related parametric test: F test. Analogous nonparametric test(s):Jonckheere test for ordered alternatives.
Friedman Two-Way Analysis of Variance This is a nonparametric two-way analysis of variance based on ranks and is a good substitute for the parametric F test when the assumptions for the F test cannot be met.
Example: Three groups of telephone employees from each of the work shifts were tested for their ability to recall fifteen-digit random numbers, under four conditions or treatments of sleep deprivation. The observations and rankings are listed in Tables 4 and 5. Is there a difference in the population medians?
Table 3 :Diet Programs and Weight-Loss Rankings
|
Group 1 |
Rank |
Group 2 |
Rank |
Group 3 |
Rank |
|
2.8 |
3 |
2.2 |
1 |
2.9 |
4 |
|
3.5 |
7 |
2.7 |
2 |
3.1 |
6 |
|
4.0 |
11 |
3.0 |
5 |
3.7 |
9 |
|
4.1 |
12 |
3.6 |
8 |
3.8 |
10 |
|
4.9 |
13 |
|
|
|
|
|
|
R, = 46 |
|
R2 = 16 |
|
R3 = 29 |
N = number of rows (subjects) (6)
k = number of columns (variables or conditions or treatments)
R. = sum of ranks in the jth column
Illustrative Assumptions: (1) There is no interaction between blocks and treatment; and (2) ordinal data with observable magnitude or interval data are needed.
Hypotheses:
H0: Md1 = Md2 = Md3 = Md4. The different levels of sleep deprivation do not have differential effects.
Hj: One or more equality is violated. The different levels of sleep deprivation have differential effects.
Test statistic or procedures: The formula and computations are listed above.
Decision: The critical value at the 0.05 level of significance in this case for N=3 and k=4 is 7.4. Reject the null hypothesis because the F value is higher than the critical value. Conclude that the ability to recall is affected.
Efficiency: The asymptotic relative efficiency of this test depends on the nature of the underlying population distribution. With k=2 (number of samples), the asymptotic relative efficiency is reported to be 0.637 relative to the t test and is higher in cases of larger number of samples. In the case of three samples, for example, the asymptotic relative efficiency increases to 0.648 relative to the F test, and in the case of nine samples it is at least 0.777.
Related parametric test: F test.
Analogous nonparametric tests: Page test for ordered alternatives.
Mann-Whitney-Wilcoxon Test A combination of different procedures is used to calculate the probability of two independent samples being drawn from the same population or two populations with equal means. This group of tests is analogous to the t-test, it uses rank sums, and it can be used with fewer assumptions.
Example: Table 6 lists the verbal ability scores for a group of boys and a group of girls who are less than 1 year old. (The scores are arranged in ascending order for each of the groups.) Do the data provide evidence for significant differences in verbal ability of boys and girls?
Table 4:Scores of Three Groups by Four Levels of Sleep Deprivation
|
Conditions |
I |
II |
III |
IV |
|
Group 1 |
7 |
4 |
2 |
6 |
|
Group 2 |
6 |
4 |
2 |
9 |
|
Group 3 |
10 |
3 |
2 |
7 |
Illustrative Assumptions: (1) Samples are independent and (2) ordinal data.
Hypotheses: A two-sided test is used in this example.
Test statistic or procedures: Rearrange all the scores in an ascending or descending order (see Table 7). The test statistics are U1 and U2 and the calculations are illustrated below.
Mann-Whitney Wilcoxon U Test The following formulas may be used to calculate U.
Decision: Retain null hypothesis. At the 0.05 level, we fail to reject the null hypotheses of no differences in verbal ability. The rejection region for U in this case is 4 or smaller, for sample sizes of 4 and 9 respectively.
Table 5:Rank of Three Groups by Four Levels of Sleep Deprivation
|
Ranks |
I |
II |
III |
IV |
|
Group 1 |
4 |
2 |
1 |
3 |
|
Group 2 |
3 |
2 |
1 |
4 |
|
Group 3 |
4 |
2 |
1 |
3 |
|
R |
11 |
6 |
3 |
10 |
Efficiency: For large samples, the asymptomatic relative efficiency approaches 95 percent.
Related Parametric Test: F test.
Analogous Nonparametric Tests: Behrens-Fisher problem test, robust rank-order test.
Z can be used as a normal approximation if N > 12, or N1, or N2 > 10, and the formula is given below.
Dispersion. Dispersion refers to spread or variability. Dispersion measures are intended to test for equality of dispersion in two populations.
The two-tailed null hypothesis in the Ansari-Bradley-type tests and Moses-type tests assumes that there are no differences in the dispersion of the populations. The Ansari-Bradley test assumes equal medians in the population. The Moses test has wider applicability because it does not make that assumption.
Dispersion tests are not widely used because of the limitations on the tests imposed by the assumptions and the low asymptotic related efficiency of the tests, or both.
Goodness-of-Fit. A goodness-of-fit test is used to test different types of problems—for example, the likelihood of observed sample data’s being drawn from a prespecified population distribution, or comparisons of two independent samples being drawn from populations with a similar distribution. The first problem mentioned above is illustrated here using the chi-square goodness-of-fit procedures.
Table 6:Verbal Scores for Boys and Girls Less than 1 Year Old
|
Boys N1 (sample A): |
10 |
15 |
18 |
28 |
|
|
|
|
|
|
Girls N2 (sample B): |
12 |
14 |
20 |
22 |
25 |
30 |
30 |
31 |
32 |
X2, or the chi-square test, is among the most widely used nonparametric tests in the social sciences. The four major types of analyses conducted through the use of chi-square are: (1) goodness-of-fit tests, (2) tests of homogeneity, (3) tests for differences in probability, and (4) test of independence. Of the four types of tests, the last one is the most widely used. The goodness-of-fit test and the test of independence will be illustrated in this article because the assumptions, formulas, and testing procedures are very similar to one another. The X2 test for independence is presented in the section on measures of association.
Goodness-of-fit tests would be used in making decisions based on the prior knowledge of the population; for example, sentence length in a new manuscript could be compared with other works of an author to decide whether the manuscript is by the same author; or a manager’s observation of a greater number of accidents in the factory on some days of the week as compared to the average figures could be tested for significant differences. The expected frequency of accidents given in table 8 below is based on the assumption of no differences in the number of accidents by days of the week.
Illustrative Assumptions: (1) The data are nominal or of a higher order such as ordinal, categorical, interval or ratio data. (2) The data are collected from a random sample.
Hypothesis:
Test Statistic or Procedures: The formula for calculating this is the same as for the chi-square test of independence. A short-cut formula is also provided and is used in this illustration:
H0 : The distribution of accidents during the week is uniform.
H1: The distribution of accidents during the week is not uniform.
The notation f0 refers to the frequency of actual observations and fe is the frequency of expected observations.
Decision: With seven observations, there are six degrees of freedom. The value for %v2 is 12.59 at the .05 level of significance. Therefore, the null hypothesis of equal distribution of accidents over the 7 days is rejected at the .05 level of significance.
Asymptotic Relative Efficiency: There is no discussion in the literature about this because nominal data can be used in this analysis and the test is often used when there are no alternatives available. Asymptotic relative efficiency is meaningless with nominal data.
Related Parametric Test. t test.
Analogous Nonparametric Tests. The Kolmogrov-Smirnov one-sample test, and the binomial test for dichotomous variables.
The Kolmogrov-Smirnov test is another major goodness-of-fit test. It has two versions, the one-sample and the two-sample tests. It is different from the chi-square goodness-of-fit in that the Kolmogrov-Smirnov test, which is based on observed and expected differences in cumulative distribution functions and can be used with individual values instead of having to group them.
Table 7:Ranked Verbal Scores for Boys and Girls Less than 1 Year Old
|
Scores: |
10 |
12 |
14 |
15 |
18 |
20 |
22 |
25 |
28 |
30 |
30 |
31 |
32 |
|
Rank: |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10.5 |
10.5 |
12 |
13 |
|
Comp: |
A |
B |
B |
A |
A |
B |
B |
B |
A |
B |
B |
B |
B |
Association. There are two major types of measures of association. They consist of: (1) measures to test the existence (relationship) or nonex-istence (independence) of association among the variables, and (2) measures of the degree or strength of association among the variables. Different tests of association are utilized in the analysis of nominal and nominal data, nominal and ordinal data, nominal and interval data, ordinal and ordinal data, and ordinal and interval data.
Chi-Square Test of Independence In addition to goodness-of-fit, %2 can also be used as a test of independence between two variables. The test can be used with nominal data and may consist of one or more samples.
Example: A large firm employs both married and single women. The manager suspects that there is a difference in the absenteeism rates between the two groups. How would you test for it? Data are included in Table 9.
Illustrative Assumptions: (1) The data are nominal or of a higher order such as ordinal, categorical, interval, or ratio data. (2) The data are collected from a random sample.
Hypothesis:
Test statistic or procedures: The formula for %2 is given below. Differences between observed and expected frequencies are calculated, and the resultant value is indicated below.
The expected frequencies are obtained by multiplying the corresponding column marginal totals by row marginal totals for each cell divided by the total number of observations. For example, the expected frequency for the cell with an observed frequency of 40 is (100 x 100)/400=25.
H0: The two variables are independent or there is no difference between married and single women with respect to absenteeism.
Hj The two variables are not indepen- (18) dent (i.e., they are related), or there is no difference between married women and single women with respect to absenteeism.
Similarly, the expected frequency for the cell with an observed frequency of 170 is (200 x 300)/ 400=150.
Decision: As the critical %2 value with two df is 5.99, we reject the null hypothesis, at the 0.05 level. We accept the alternate hypothesis of the existence of a statistically significant difference in the ratio of absenteeism per year between the two groups of married and single women.
Efficiency: The asymptotic relative efficiency of a x2 test is hard to assess because it is affected by the number of cells in the contingency table and the sample size as well. The asymptotic related efficiency of a 2 x 2 contingency table is very low, but the power distribution of %2 starts approximating closer to 1 as the sample size starts getting larger. However, a large number of cells in a %2 table, especially with a combination of large sample sizes, tend to yield large %2 values which are statistically significant because of the size of the sample. In the past, Yate’s correction for continuity was often used in a 2 x 2 contingency table if the cell frequencies were small. Because of the criticism of this procedure, this correction procedure is no longer widely used. Other tests such as Fisher’s Exact Test can be used in cases of small cell frequencies.
Table 8:Frequency of Traffic Accidents for One Week during May
|
Day |
S |
M |
T |
W |
T |
F |
S |
Total |
|
Traffic Accidents |
15 |
30 |
30 |
25 |
25 |
40 |
45 |
210 |
|
Expected Frequencies |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
210 |
Related Parametric Test: There are no clear-cut related parametric tests because the %2 test can be used with nominal data.
Analogous Nonparametric Tests: The Fisher Exact Test (limited to 2 x 2 tables and small tables) and the median test (limited to central tendencies) can be used as alternatives. In addition, a large number of tests such as phi, gamma, and Cramer’s V statistic, can be used as alternatives, provided the data characteristics meet the assumptions of these tests. The %2 distribution is used in many other nonparametric tests.
The chi-square tests of contingency tables allow partitioning of tables, combining tables, and using more than two-way tables with control variables.
The second type of association tests measure the actual strength of association. Some of these tests also indicate the direction of the relationship and the test values in most cases extend from -1.00 to +1.00 indicating a negative or a positive relationship. The values of some other nondirectional tests fall between 0.00 and 1.00. Contingency table formats are commonly used to measure this type of association. Among the more widely used tests are the following, arranged by the types of data used: Nominal by Nominal Data:
Phi coefficient—limited to a 2 x 2 contingency table. A square of these test values is used to interpret a proportional reduction error.
Contingency coefficient based on the chi-square values. The lowest limit for this test is 0.00, but the upper limit does not attain unity (value of 1.00).
Cramer’s V statistic—not affected by an increase in the size of cells as long as it is related to similar changes in the other cells.
Lambda—the range of lambda is from 0.00 to 1.00, and thus it has only positive values.
Ordinal by Ordinal Data:
Gamma—uses ordinal data for two or more variables. Test values are between -1.00 and +1.00.
Somer’s D—used for predicting a dependent variable from the independent variable.
Kendall’s tau—described in more detail below.
Spearman’s rho—described in more detail below.
Categorical by Interval Data
Kappa—The table for this test needs to have the same categories in the columns and the rows. Kappa is a measure of agreement, for example, between two judges.
The tests described above are intended for two-dimensional contingency tables. Tests for three-dimensional tables have been developed recently in both parametric and nonparametric statistics.
Two other major measures of association referenced above are presented below. They are Kendall’s T (the forerunner of this test is also one of the oldest test statistics) and Spearman’s p (one of the oldest nonparametric techniques). They are measures of association based on ordinal data.
Table 9:Annual Absences for Single and Married Women
|
Days Absent |
Married Women |
Single Women |
Row Totals |
||
|
|
fo |
(fe) |
fo |
(fe) |
|
|
Low (0-5) |
30 |
(25) |
70 |
(75) |
1 00 |
|
Medium (6-10) |
40 |
(25) |
60 |
(75) |
100 |
|
High (11+) |
30 |
(50) |
170 |
(150) |
200 |
|
Column Totals |
|
100 |
|
300 |
400 |
T is a measure of rank-order correlation. It also tests for independence of the two variables observed. It assumes at least ordinal data. The test scores of T range between -1.00 and +1.0 by convention. A score of+1.00 indicates a perfect agreement between rankings of the two sets of observations. A score of -1.00 indicates a perfect negative correlation which means the ranking in one observation is in the reverse order of the other set of observations. All other scores fall between these two values. The test statistics for data with no ties is given below.
The test statistic:
S measures the difference between the pairs of observations in natural order. A number of students are ranked according to their mathematical and verbal test scores. The six students are identified by letters A to F. There is no need to know the actual scores, and if actual scores are known, they will be converted to ranks as in Table 10.
What is being measured here with T is the degree of correspondence between the two rankings based on mathematical and verbal scores. The calculations can be simplified if one of the values is arranged in the natural ascending order from the lowest value to the highest value. The lack of correspondence between the two rankings can be measured by just using the second set of rankings which, in this case, is verbal ability.
Illustrative Assumptions: (1) The data are at least ordinal. (2) Variables in the study are continuous.
Hypothesis:
H0 : Mathematical and verbal test scores are independent.
Hj: Mathematical and verbal test scores are related positively or negatively.
The number of concordant pairs is measured by the agreement between the two pairs based on their corresponding standing in their own ranking, and discordant pairs are calculated on the basis of the disagreement between them. The example given below in Table 11 consists of no tied ranks.
Decision: With n = 6, the researcher fails to reject the null hypothesis H0 at 0.05 level since tau = 0.067 is smaller than tau = 0.600, which is the critical value for a two-tailed test.
Efficiency: The asymptotic relative efficiency: Both Kendall’s T and Spearman’s p have an asymptotic relative efficiency of .912 compared to the Personian r (correlation coefficient) which is a parametric test and can go up to 1.12 in exponential type of distribution data.
Related Parametric Test: Personian correlation coefficient (in case of interval or ratio data).
Analogous Nonparametric Tests: Spearman’s p (rho).
Table 10:Mathematical (X) and Verbal (Y) Test Scores for Six Students
|
|
A |
B |
C |
D |
E |
F |
|
X Math |
9 |
15 |
8 |
10 |
12 |
7 |
|
Y Verbal |
10 |
13 |
9 |
11 |
4 |
12 |
In many studies, however, the same values may occur more than once within X observations, within Y observations, or within both observations—in which case there will be a tie. In the case of tied ranks, different formulas for taua, taub, tauc are used. There is, however, no general agreement in the literature about the usage of subscripts. More detailed treatment of this topic is provided in Kendall and Gibbons (1990). Kendall’s T measures the association between two variables, and when there are more than two variables, Kendall’s coefficient of concordance can be used to measure the association among multiple variables.
Spearman’s p (rho) is another popular measure of a rank-correlation technique. The technique is based on using the ranks of the observations, and a Personian correlation is computed for the ranks. Spearman’s rank correlation coefficient is used to test independence between two rank-ordered variables. It resembles Kendall’s tau in that regard, and the two tests tend to be similar in their results of hypothesis testing.
Runs and Randomness. A run is a gambling term that in statistics refers to a sequence or an order of occurrence of event. For example, if a coin were tossed ten times, it could result in the following sequence of heads and tails: H T H H H T T H H T. The purpose of runs test is to determine whether the run or sequence of events occurs in a random order.
Another type of runs test would be to test whether the run scores are higher or lower than the median scores. A runs up-and-down test compares each observation with the one immediately preceding it in the sequence. Runs tests are not very robust, as they are very sensitive to variations in the data.
As there are no direct parallel parametric tests for testing the random order or sequence of a series of events, the concept of power or efficiency is not really relevant in the case of runs tests.
Regression. The purpose of regression tests and techniques is to predict one variable based on its relationship with one or more other variables. The procedure most often used is to try to fit a regression line based on observed data. Though only a few simple regression techniques are included in Table 1, this is one of the more active areas in the field of nonparametric statistics.
The problems relating to regression analysis are similar to those in parametric statistics such as finding a slope, finding confidence intervals for slope coefficients, finding confidence intervals for median differences, curve fitting, interpolation, and smoothing. For example, the Brown-Mood method for finding a slope consists of graphing the observations on a scatter diagram; then a vertical line is drawn representing the median value, and points on both sides of the vertical line are joined. This gives the initial slope, which is later modified through iterative procedures if necessary. Some other tests are based on an extension of the rank order of correlation techniques discussed earlier.
Trends and Changes. Comparisons between, before, and after experiment scores are among the most commonly used procedures of research designs. The obvious question in such cases is whether there is a pattern of change and, if so, whether the trends can be detected. Demographers, economists, executives in business and industry, and federal and state departments of commerce are always interested in trends—whether downward, upward, or existing at all. The Cox-Stuart change test, or test for trend, is a procedure intended to answer these kinds of questions. It is a modification of the sign test. The procedures are very similar to the sign test.
Table 11:Mathematical (X) and Verbal (Y) Test Scores in Rank Order
|
|
|
(Y is similar |
Y is reverse |
|
Values |
Rankings |
in natural |
of natural |
|
(X, Y) |
(X, Y) |
order to X) |
order of X) |
|
(7, 12) |
(1, 5) |
1 |
4 |
|
(8, 9) |
(2, 2) |
3 |
1 |
|
(9, 10) |
(3, 3) |
2 |
1 |
|
(10, 11) |
(4, 4) |
1 |
1 |
|
(12, 4) |
(5,1) |
1 |
0 |
|
(15, 13) |
(6, 6) |
0 |
0 |
|
|
|
8 |
7 |
Example: We want to test a statement in the newspaper that there is no changing trend in snowfall in Seattle between the last twenty years and the twenty years before that. The assumptions, procedures, and test procedures are similar to the sign test. These data constitute twenty sets of paired observations. If the data are not chronological, then values below the median and above the median would be matched in order. The value in the second observation in the set is compared to the first and would be coded as either positive or plus, negative or minus, and no change. A large number of positive or negative signs would indicate a trend, and the same number of positive and negative signs would indicate no trend. The distribution here is dichotomous, and, hence, a binomial test would be used. If there are seven positive signs and thirteen negative signs, it can be concluded that there is no statistically significant upward or downward trend in snowfall at the 0.05 level as p(k = 7/20/0.50) is greater, k being the number of positive signs. The asymptotic relative efficiency of the test compared to rank correlation is 0.79. Spearman’s coefficient of rank correlation and Kendall’s Tau may also be used to test for trends.
Proportion. The term ”portion” or the term ”share” may be used to convey the same idea as ”proportion” in day-to-day usage. A sociologist might be interested in the proportion of working and nonworking mothers in the labor force, or in comparing the differences in the proportion of people who voted in a local election and the voter turnout in a national election. In case of a dichotomous situation, a binomial test can be used as a test of proportion; but there are many other situations where more than two categories and two or more independent samples are involved. In such cases, the chi-square distribution may also be viewed as a test of differences in proportion between two or more samples.
Cochran’s Q test is another test of proportions that is applicable to situations with dichotomous choices or outcomes for three or more related samples. For example, in the context of an experimental situation, the null hypothesis would be that there is no difference in the effectiveness of treatments. Restated, it is a statement of equal proportions of success or failures in the treatments.
NEW DEVELOPMENTS
The field of nonparametric statistics has matured, and the growth of the field has slowed down compared to the fast pace in the 1940s and 1950s. Among the reasons for some of these changes are the development of new techniques in parametric statistics and log linear probability models, such as logit analysis for categorical data analysis, and the widespread availability of computers that perform lengthy calculations. Log linear analysis has occasionally been treated in nonparametric statistics literature because it allows the analysis of dichoto-mous or ordered categorical data and allows the application of nonparametric tests. As indicated earlier, it was not included in the tests discussed in this article because it is a categorical response analog to regression or variance models.
There is further research being conducted in the field of nonparametric robust statistics. The field of robust statistics is also in the process of developing into a new subspecialty of its own. At the same time, development of new tools—jack-knife, bootstrapping, and other resampling techniques that are used both in parametric and nonparametric statistics—has positively impacted the use of nonparametric techniques. Based on the contents of popular computer software, the field of nonparametric statistics cannot yet be considered part of the mainstream of statistics, although some individual nonparametric tests are widely used.
There are many new developments taking place in the field of nonparametric statistics. Only three major trends are referenced here. The scope of application of nonparametric tests is gradually expanding. Often, more than one nonparametric test may be available to test the same or similar hypotheses. Again, many new, appropriate, and powerful nonparametric tests are being developed to replace or supplement the original parametric tests. Last, new techniques such as bootstrapping are making nonparametric tests more versatile.
As in the case of bootstrapping, many other topics and subtopics in nonparametric statistics, have developed into full-fledged specialties or subspecialties—for example, extreme value statistics, which is used in studying floods and air pollution. Similarly, a large number of new techniques and concepts—such as (1) the influence curve for comparing different robust estimators, (2) M-esti-mators for generalizations that extend the scope of traditional location tests, and (3) adaptive estimation procedures for dealing with unknown distribution—are being developed in the field of inferential statistics. Attention is also being directed to the developments of measures and tests with nonlinear data. In addition, attempts are being made by nonparametric statisticians to incorporate techniques from other branches of statistics, such as Bayesian statistics.
Parallel Trends in Development. There are two parallel developments in nonparametric and parametric statistics. First, the field of nonparametric statistics is being extended to develop more tests analogous to parametric tests. Recent developments in computer software include many of the new nonparametric tests and alternatives to parametric tests. Second, the field of parametric statistics is being extended to develop and incorporate more robust tests to increase the stability of parametric tests. The study of outliers, for example, is now gaining significant attention in the field of parametric statistics as well.
Recent advancements have accelerated developments in nonparametric and parametric statistics, narrowing many distinctions and bridging some of the differences between the two types, bringing the two fields conceptually closer.