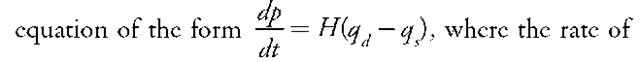Tatonnement, a concept introduced by French economist Leon Walras (1834-1910), is a trial-and-error process by which equilibrium prices and stability are reached in competitive markets. Walras found that "the markets which are best organized from the competitive standpoint are those in which purchases and sales are made by auction" (Walras 1954, pp. 83-84).
In an auction market, the tatonnement process starts when the price is fixed (called out), and then demand and supply states are revealed. One possibility is that demand and supply conditions are balanced, establishing normal prices. The most likely state is disequilibrium, where the market will show excess supply or demand, causing deviation of the actual from the natural price. If equilibrium prices are not obtained, then tatonnement requires the auctioneer to increase or lower prices, depending on the demand or supply conditions. In this groping process, the market mechanism would make the actual price gravitate to its natural level, establishing equilibrium. As long as equilibrium is not achieved, no contracts for selling or buying will be executed. The modern literature has conferred the name nontatonnement on the situation where trading does take place at false prices. An unsolved problem with the tatonnement process is whether to make it compatible with the solutions of equation systems by counting equations and unknowns as Walras did, or through more complex general equilibrium solutions such as fixed-point methods.
Walras’s analysis of the tatonnement process was challenging because both equilibrium levels and stability conditions were required. Walras compared the stability analysis to a pendulum-like mechanism in which "the center of gravity lies directly beneath the point of suspension, so that if this center of gravity were displaced from the vertical line beneath the point of suspension, it would automatically return" (1954, pp. 109-112). That concept of stability remains in vogue. John Hicks’s (1904-1989) research (1946) was an early attempt to make Walras’s arguments transparent to economists. With two commodities, X and Y, Hicks explained that equilibrium required that the supply of X be equal to the demand for X. Stability requires that a fall in the relative price of X to Y, which will make X cheaper, will increase the demand for X above its supply. For multiple commodities, Hicks realized that when the relative price of X to a standard commodity changed, we need to know what will happen to the prices of the other commodities, which can be assumed fixed, or assumed to move to their equilibrium levels. The classical economist Alfred Marshall (1842-1924) simplified this with his introduction of ceteris paribus assumption, which held changes in all other prices constant.
Paul Samuelson improved the process by making Hicks’s contribution more dynamic. For a one-commodity case, Samuelson (1941, p. 102) wrote a price differential
allowing the demand and supply variables to depend on the prices of say n commodities, p1, …, p . In the commodities case, the model implies that if we plot excess demand for good 1 against the relative prices, p1/p2, we obtain solutions for the prices when the excess demand function crosses the relative price axis. Stable conditions are obtained only when the excess demand cuts the relative price axis from above, implying that the excess demand function is downward. Stability is obtained because if the actual price ratio is higher than the equilibrium price ratio, then excess supply of good 1, and excess demand for good 2, are obtained, and prices will adjust accordingly so that the actual price ratio goes back to equilibrium.
For more than two goods, the Samuelsonian development of the tatonnement process cannot be generalized. While Samuelson improved upon Hicks’s model in the dynamic realm, his correspondence principle shows that static and dynamic relations are both useful concepts. Samuelson (1960, p. 368) also developed the Le Chatelier principle to explain adjustment to equilibrium after an initial displacement. Increases in demand will cause the relative price, say, of goods Hn to increase. If the prices of the other goods, Hn _ 1, increase, then it will lower the increase in the price of H . The increased price of H will be smaller if the price of Hn _ 2 is also unchanged. The metaphor for this process is that squeezing a balloon will decrease its volume more with constant temperature than if we let its temperature warm up during the squeezing.
As Franklin Fisher (2006, pp. 143-144) pointed out, this treatment represents the tatonnement process when only prices adjust and trade does not take place at disequilibrium prices. The solution is, therefore, unsatisfactory,because many prices are fixed and auctioneers are not present in all markets.