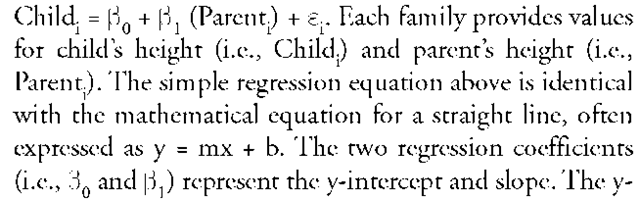Regression is a broad class of statistical models that is the foundation of data analysis and inference in the social sciences. Moreover, many contemporary statistical methods derive from the linear regression model. At its heart, regression describes systematic relationships between one or more predictor variables with (typically) one outcome. The flexibility of regression and its many extensions make it the primary statistical tool that social scientists use to model their substantive hypotheses with empirical data.
HISTORY AND DEFINITION
The original application of regression was Sir Francis Galton’s study of the heights of parents and children in the late 1800s. Galton noted that tall parents tended to have somewhat shorter children, and vice versa. He described the relationship between parents’ and children’s heights using a type of regression line and termed the phenomenon regression to mediocrity. Thus, the term regression described a specific finding (i.e., relationship between parents’ and children’s heights) but quickly became attached to the statistical method.
The foundation of regression is the regression equation; for Galton’s study of height, the equation might be:
intercept estimates the average value of children’s height when parent’s height equals 0, and the slope coefficient estimates the increase in average children’s height for a 1-inch increase in parent’s height, assuming height is measured in inches. The intercept and slope define the regression line, which describes a linear relationship between children’s and parents’ heights. Most data points (i.e., child and parent height pairs) will not lie directly on the simple regression line; the scatter of the data points around the regression line is captured by the residual error term &, which is the vertical displacement of each datum point from the regression line.
The regression line describes the conditional mean of the outcome at specific values of the predictor. As such, it is a summary of the relationship between the two variables, which leads directly to a definition of regression: "[to understand] as far as possible with the available data how the conditional distribution of the response … varies across subpopulations determined by the possible values of the predictor or predictors" (Cook and Weisberg 1999, p. 27). This definition makes no reference to estimation (i.e., how are the regression coefficients determined?) or statistical inference (i.e., how well do the sample coefficients reflect the population from which they were selected?). Historically, regression has used least-squares estimation (i.e., coefficient values are found that minimize the squared errors &) and frequentist inference (i.e., variability of sample regression coefficients are examined within theoretical sampling distributions and summarized by p-values or confidence intervals). Although least-squares regression estimates and p-values based on frequentist inference are the most common default settings within statistical packages, they are not the only methods of estimation and inference available, nor are they inherently aspects of regression.
EXTENSIONS OF THE BASIC REGRESSION MODEL
If regression only summarized associations between two continuous variables, it would be a very limited tool for social scientists. However, regression has been extended in numerous ways. An initial and important expansion of the model allowed for multiple predictors and multiple types of predictors, including continuous, binary, and categorical. With the inclusion of categorical predictors, statisticians noted that analysis of variance models with a single error term and similar models are special cases of regression, and the two methods (i.e., regression and analysis of variance) are seen as different facets of a general linear model.
A second important expansion of regression allowed for different types of outcome variables such as binary, ordinal, nominal, and count variables. The basic linear regression model uses the normal distribution as its probability model. The generalized linear model, which includes non-normal outcomes, increases the flexibility of regression by allowing different probability models (e.g., binomial distribution for binary outcomes and Poisson distribution for count outcomes), and predictors are connected to the outcome through a link function (e.g., logit transformation for binary outcomes and natural logarithm for count outcomes).
Beyond the general and generalized linear models, numerous other extensions have been made to the basic regression model that allow for greater complexity, including multivariate outcomes, path models that allow for multiple predictors and outcomes with complex associations, structural equation models that nest measurement models for latent constructs within path models, multilevel models that allow for correlated data due to nested designs (e.g., students within classrooms), and nonlinear regression models that use regression to fit complex mathematical models in which the coefficients are not additively related to the outcome. Although each of the preceding methods has unique qualities, they all derive from the basic linear regression model.
REGRESSION AS A TOOL IN SOCIAL SCIENCE RESEARCH
Research is a marriage of three components: Theory-driven research questions dictate the study design, which in turn dictates the statistical methods. Thus, statistical methods map the research questions onto the empirical data, and the statistical results yield answers to those questions in a well-designed study. Within the context of scientific inquiry, regression is primarily an applied tool for theory testing with empirical data. This symbiosis between theoretical models and statistical models has been the driving force behind many of the advances and extensions of regression discussed above.
Although regression can be applied to either observational or experimental data, regression has played an especially important role in observational data. With observational data there is no randomization or intervention, and there may be a variety of potential causes and explanations for the phenomenon under study. Regression methods allow researchers to statistically control for additional variables that may influence the outcome. For example, in an observational study of infidelity that focuses on age as a predictor, it might be important to control for relationship satisfaction, as previous research has suggested it is related to both the likelihood of infidelity and age. Because regression coefficients in multiple regression models are estimated simultaneously, they control for the presence of the other predictors, often described as partialing out the effects of other predictors.
Regression can also play a practical role in conveying research results. Regression coefficients as well as regression summaries (e.g., percentage of the outcome variability explained by the predictors) quantitatively convey the importance of a regression model and consequently the underlying theoretical model. In addition, regression models are prediction equations (i.e., regression coefficients are scaling factors for predicting the outcome based on the predictors), and regression models can provide estimates of the outcome based on predictors, allowing the researcher to consider how the outcome varies across combinations of specific predictor values.
LIMITATIONS
Even though regression is an extremely flexible tool for social science research, it is not without limitations. Not all research questions are well described by regression models, particularly questions that do not specify outcome variables. As an example, cluster analysis is a statistical tool used to reveal whether there are coherent groups or clusters within data; because there is no outcome or target variable, regression is not appropriate. At the same time, because regression focuses on an outcome variable, users of regression may believe that fitting a regression model connotes causality (i.e., predictors cause the outcome). This is patently false, and outcomes in some analyses may be predictors in others. Proving causality requires much more than the use of regression.
Another criticism of regression focuses on its use for statistical inference. To provide valid inference (e.g., p-val-ues or confidence intervals), the data must be a random sample from a population, or involve randomization to a treatment condition in experimental studies. Most samples in the social sciences are samples of convenience (e.g., undergraduate students taking introductory psychology). Of course, this is not a criticism of regression per se, but of study design and the limitations of statistical inference with nonrandom sampling. Limitations notwithstanding, regression and its extensions continue to be an incredibly useful tool for social scientists.