Physical parameters and models of the ZL
The variables of interest in the interplanetary medium are the number density, size, shape and albedo of the particles, their distance from the Sun, and their speed and direction of motion, almost all of which may be a function of any of the others. In addition, we would like to know the chemical composition of the material, what proportion is gas and what dust, what are its rates of evaporation, melting points, and degree of ionisation and so on. The reason for the slow progress in early ZL research is immediately apparent, since any model constructed to fit a comparatively small range of possible experimental measurements is required to yield values of an enormous number of interconnected physical variables. Simple models of the Zodiacal Cloud are based on number density as a function of position in the Solar System and particle radius.
Some early observers attempted to attribute the existence of the ZL to scattering of light in the Earth’s atmosphere, or (as favoured by Jones in 1865) from a dust cloud centred on the Earth; but even in 1683 Cassini had suggested that its appearance might be due to sunlight scattered by a lens-shaped (lenticular) circumsolar cloud of dust concentrated in the plane of the planets, the Earth being situated some way out towards the edge of the ‘lens’. This, aside from some exciting recent discoveries about the fine structure of the cloud – zones, or bands, of concentration of material attributed to asteroidal erosion and planetary gravitation – is roughly the view of most astronomers today, though there is still a lingering doubt as to whether a component might be attributed to a Geocentric Dust Cloud (GDC). The Geocentric Theory, though not popular by 1970, still had its adherents (Peale 1966; Divari 1965 and 1966). Early satellite measurements of particle densities seemed to give support to the existence of a significant dust cloud extending to a few Earth radii, giving cause for alarm to those contemplating manned exploration of Space. However, these were later shown to be suspect by Nilsson and Southworth (1967). These researchers, in 1972, detected only TWO impacts in their detector tubes aboard the OGO 2 satellite in hundreds of hours, and the reality of even these was in doubt! So they were able to put an upper limit on micrometeoroids in the vicinity of the Earth of mass greater than 10-12g, of 0.01 particles per cubic metre per second (1967). Indeed these early reports of high concentrations of dust in the region of the Earth were never since confirmed, though we shall see later (1.2.4) that there now seems to be evidence for at least a circumsolar band of dust in the region of the Earth’s orbit. Searches for parallax effects in the ZL axis dependent on the observer’s latitude yielded conflicting results (perhaps hardly surprising given the difficulty of correcting for atmospheric extinction, and the extreme difficulty of seeing the ZL at all in high latitudes). Roosen (1970) failed to detect the Earth’s shadow passing through the Gegenschein, an effect which ought to have been detectable if the dust were near to the Earth (except on one occasion, when a comet was held to be responsible). Roosen also established that the predicted L5 cloud, at the Earth-Moon Libration point, was non-existent. The exhaustive theoretical treatment of Shapiro, Lautman and Columbo (1967) concluded that the existence of a significant GDC is ‘unlikely’.
Most researchers now favour circum-solar models, and these have frequently used ZL photometry and polarimetry measurements as their starting points (Behr and Seidentopf 1953; Divari and Asaad 1959; Ingham 1961). Ingham included solar corona data, and fitted parameters to a compromise curve, since there was some difficulty in bridging the two sets of data. The general method, in fitting models to experimental findings, is to make certain simplifying assumptions about the particles (typically spherical particles in circular orbits, with uniform specific gravity and albedo), to restrict attention to the plane of the ecliptic, and to assume values of some parameters, in order to make a suitable fit to the observations by adjustment of the others.
A representative model is one in which the albedo (ratio of reflected light to incident light) of the particles:
and the dependence of number density (n) on particle radius (a) and distance from the Sun (r) has the form:
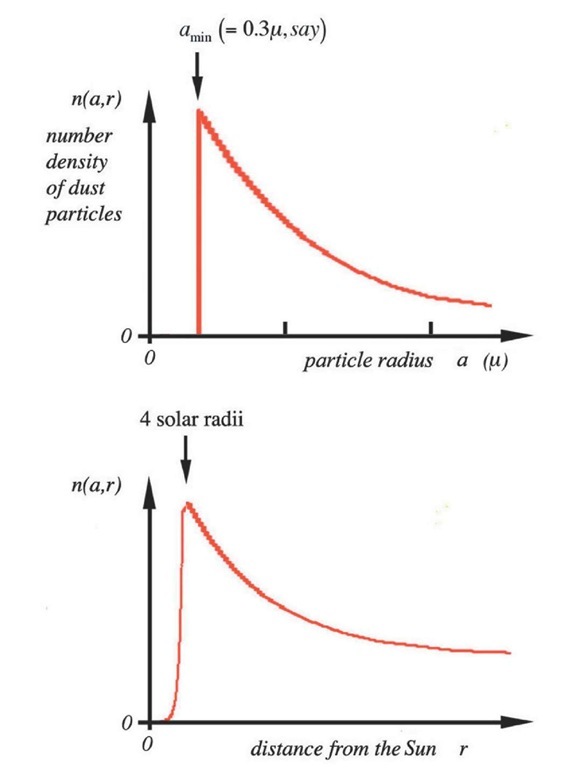
This is already, evidently, a simplified model, since in reality there is no reason to suppose that p and a are constant, or even orthogonal with each other. The value of no is chosen so as to give a total number density of 240 particles per cubic km at 1 AU from the Sun, and a lower limit of 0.3 microns is imposed on the particle radius. This is because very small particles are ejected from the Solar System by the pressure of sunlight (Giese 1961); the value of amin can in fact be 0.2 microns to 0.4, depending on the density of the particle, which is usually estimated as between 1 and 3 g/cm3 . Further, particles less than 0.2 microns in radius would scatter light selectively according to wavelength, giving rise to predictions of colourations in the ZL which have not been observed, though, again, observations are not all in agreement. In this analysis, the particles are large compared with the wavelength of light under discussion, so the complex theory of Mie Scattering is not needed. Values of p between 0 and 5 were favoured by Weinberg (1965) and also by Ingham (1961), from photometry and polarimetry measurements (see Figure 1.4).
Turning attention to the dependence of n on distance from the Sun, Over (1958) predicted a dust-free zone within about 4 solar radii (4 rs) owing to vaporisation by the Sun. Infrared emission peaks were reported by Petersen (1967) supporting the prediction. This can be incorporated in the model by specifying two domains for relation 1.1, an inner one (r < 4 solar radii) in which n(a, r) varies as
/ \—a
(4 rs — r) where a is large, and the outer region where the model is as before (Figure 1.4).
Most in situ ZL measurements in this period were made from satellites in the neighbourhood of the Earth, and served to verify and extend the Earth-bound data. Hanner and Weinberg (1973) conducted an interesting experiment in which measurements were made of the Gegenschein intensity as a function of distance from the Sun from an outgoing space vehicle. Their results lent support to the model:
The reason why the Gegenschein is there at all was certainly not clear prior to 1970, and may still be in question. If it is not due to a GDC, or to Lunar ejecta streaming outwards in the solar wind (Jeffries 1971), perhaps n(r) in the circumsolar cloud increases outside the Earth’s orbit, or perhaps the effect is caused by a back-scattering peak in intensity which might be expected from ‘fluffy’ particles, and has been predicted from models using dielectric materials in general. In none of the above scenarios is the observed shape of the localised maximum at the antisolar point easy to explain.
Before leaving this sketch of the state ZL knowledge in 1970-4, when my experiment took place, it is interesting to note that the era of space-borne observations of the interplanetary medium was just beginning, and at this stage, things were not going as well as might have been hoped! Sparrow and Ney (1973), based on data from OSO-5, concluded that there was essentially no variation in the brightness or the polarisation of the ZL from 1969 to 1973. Levasseur and Blamont (1973), on the other hand, using data from satellite OS2 "Tournasol" disagreed entirely. It might be interesting (but outside the scope of this work) to revisit these two papers in the light of what we now know from the 1984 IRAS revelations. This, coupled with the similarly inconclusive results of particle collection mentioned earlier, set a tone of uncertainty in the results of in situ studies, which around 1970 gave good reason to persist in Earth-based research on the ZL, in particular with the relatively new technique of Doppler radial velocity measurements.
Figure 1.4 A simple model of Zodiacal dust density as a function of particle radius and distance from the Sun.
Doppler investigations of the ZL prior to 1970
The approach of radial velocity measurement is especially valuable in the study of the ZL, since it provides completely independent estimates of some of the parameters – viz. speed and direction distributions in the cloud, leading to insights into its formation and evolution.
Christian Doppler, an Austrian mathematician and physicist working in Prague, was the first to draw attention to the change of the pitch of sound waves due to a relative motion of the emitter and the observer, an effect very noticeable in the siren noise on a passing police car, and thereafter known as the Doppler effect. He was able to offer an explanation, in terms of the way the wavelengths perceived by the observer were ‘squeezed or stretched’ by the relative motion, and proposed, in his paper in 1842, translated as "On the Coloured Light of Double Stars and Certain Other Stars of the Heavens", that a similar effect would be seen with light waves. It is easy to visualise that light waves emitted from a moving source are squeezed closer together (as perceived by us) if the source is approaching us, producing a shift in wavelength to the blue, and stretched out if the source is moving away, so that we see a red shift. In 1848, French astronomer Hippolyte Fizeau, the first to make a serious estimate of the speed of light, confirmed experimentally that the Doppler effect changed the positions of spectral lines, by amounts proportional to a source’s radial velocity relative to us.
The Doppler shift AX from a source of light of wavelength X, moving at a radial velocity V relative to us, is given by the simple relation
In 1862, Huggins and Miller remarked that the analysis of Fraunhofer lines in stars could lead, not only to analysis of their material compositions, but also to estimates of their motions. "If the stars were moving towards or from the Earth, their motion, compounded with the Earth’s motion, would alter to an observer on the Earth the refrangibility of the light emitted by them, and consequently the lines of terrestrial substances would no longer coincide in position in the spectrum with the dark lines produced by the absorption of the vapours of the same substances existing in the stars." Thus was born the science of spectral radial velocity measurements.
We can note in passing that the Doppler effect became a pillar of the evidence for the ‘Expanding Universe’ as we perceive it today. The above relationship was invoked by Vesto Slipher in 1917, who found that the light from the 21 of the 25 galaxies he studied showed a red shift, indicating that they were receding from us, and in 1929 Edwin Hubble was able to show that the speed of their recession was proportional to their distance from us.
Much closer to home, we have seen that Blackwell and Ingham (1961) used the concept of ‘smearing’ of absorption lines due to high Doppler shifts to place an upper limit on free electrons in the interplanetary medium. This introduced Doppler techniques to the study of the Zodiacal Light, and it was Ingham who laid the foundations for use of the Doppler method for investigations of the motions of interplanetary dust.
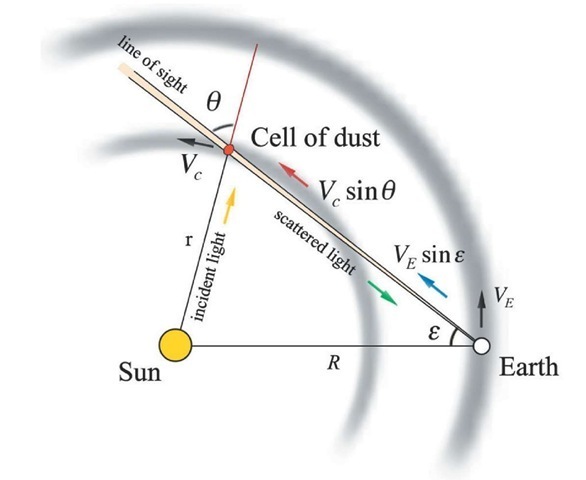
The profile of an absorption feature in the ZL spectrum in a particular area of sky corresponds to a unique line of sight through the Zodiacal Cloud, and is a combination of the effects of all the light-scattering dust particles along this line. We can regard the spectrum as the summation of contributions from all the elements, or ‘cells’ in the line of sight; each has a radial velocity relative to the Earth which is a combination of its own motion and that of the Earth, and leaves its ‘signature’ on the resulting combined spectrum. By comparing such a theoretical prediction with experiment, for various different directions relative to the Sun, information can be derived on relative number and size distributions and velocity distribution in the cloud, quite independently of other observations. Typical geometry applying to a radial velocity element, or ‘cell’, is shown in Figure 1.5.
This view from ‘above’ the plane of the ecliptic shows the geometry for a cell of dust, viewed from the Earth, along a line of sight at an elongation angle 8 from the Sun. In the particular case illustrated, the dust is moving with speed Vc, in a circular solar orbit, and therefore has no radial velocity relative to the Sun (in fact the orbits may not be circular, but may be nearly so). The cell ‘sees’ the continuous visible light emission spectrum of the Sun, crossed by dark Fraunhofer lines of absorption, with zero shift. Dust in the cell scatters light towards the Earth. But this cell is moving away from the Earth radially with a component of its velocity along the line of sight Vc sin0 , while the Earth’s orbital motion, velocity VE, produces an opposing, closing component of velocity along the line of sight VE sin 8. The resulting radial velocity to be used in applying the Doppler shift is thus Vc sin0 – VE sin8. We can eliminate the cell’s velocity as follows. We know that for circular orbits:
where r is the distance of the dust cell from the Sun, and R is the distance of the Earth from the Sun. In the Earth-Sun-Cell triangle the Sine Law gives:
And the required relative radial velocity ![]() is given by
is given by
Figure 1.5 Illustrating a line-of-sight integration for prediction of a Doppler-shifted absorption line spectrum from a rotating dust cloud model.
The resulting contribution of this cell to the spectrum of the ZL is light with a red shift of AX, where:
Ingham first arrived at this formula in his paper (1969) in a slightly different form, using cosecs.
An integral of this expression for all cells along the line of sight, weighted according to the predicted density of dust for each cell position, and the percentage of incident light re-directed towards the observer, gives an ‘average’ radial velocity, and hence an average wavelength shift for any absorption line, which can be compared with the shifts found by experiment. Clearly this is an approximation; a full treatment integrates the intensity at each wavelength, and predicts the profile of the absorption line in detail.
In 1963, Ingham (1963) published his theoretical predictions, calculated in this way, of the manner in which the shape of a solar Fraunhofer line would be modified by scattering from a rotating dust cloud medium (Figure 1.6), in the ecliptic plane, as a function of elongation from the Sun. He showed that a broadening and overall shift of the wavelength of the line ought to be detectable, giving information with which to map the motions of Zodiacal dust. All that was now needed was the observational evidence to compare with this theory.
Figure 1.6 Ingham’s (1963) theoretical predictions for the shape of a modified Fraunhofer line (elongation 30°) in sunlight scattered by a rotating circum-solar dust cloud.
Attempts to record a high-resolution spectrum of the ZL as a tool for revealing and discriminating between motional signatures, are limited only by the resolution-luminosity (R-L) product of the instrument and time available to spend on observing each point. The need for high R-L product was a good reason for choosing an interferometric spectrometer, the Fabry-Perot etalon (Jacquinot 1954), but as we will see, there are other attractive alternatives.
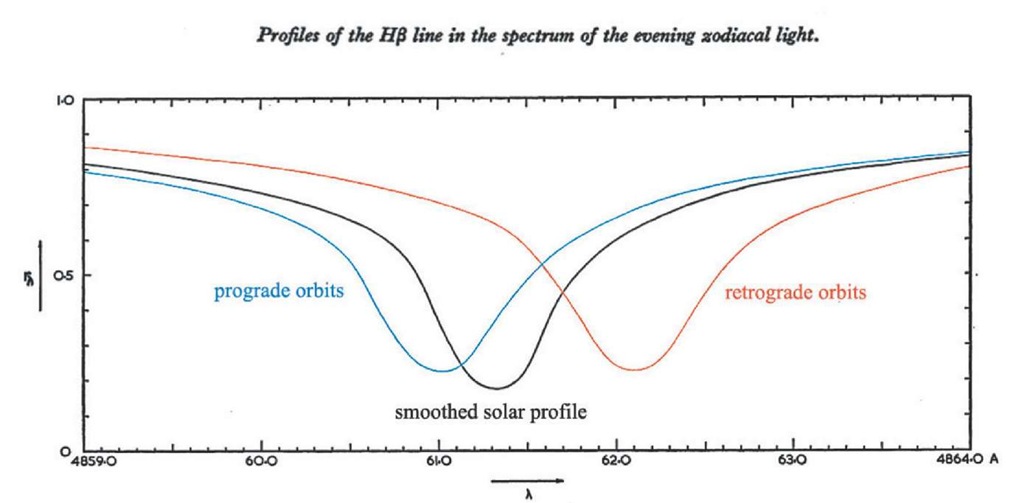
Beginning in June-August 1962, under the leadership of Professor James Ring at Chacaltaya in Bolivia, Hindle, Reay and Ring (1968) employed a Fabry-Perot etalon in series with an Ebert Spectrometer, with a resulting resolved width of about 1.2 Angstroms (A), to record Zodiacal Light spectra in the region of the Hp absorption line over a range of about 10 A, with the intention of determining Doppler shifts in this line. Detection was by cooled photomultiplier and counting electronics, a precedent followed in many subsequent experiments of this type. Instead of the absorption line they had hoped to see, they found strong evidence of Hp emission. Only a small number of observations were made, mostly of the evening ZL, and the conclusions were:
(a) That the profile of the Balmer Hp line in the spectrum of the Zodiacal Light did not match that of the Sun, either in position or shape.
(b) That some scans showed clear evidence of emission at the Hp wavelength, especially near the Galactic plane, annd it was proposed that this emission was from Hydrogen in the Galactic plane.
In 1964, Prof. Ring’s team made a new set of observations, using a 3" Fabry-Perot and an interference filter premonochromator (Daehler et al 1968). The width of the pass-band of the system was 1.5 A, and about 50 scans were obtained of morning and evening ZL. The most immediate result was the confirmation of Hp emission, which still obscured the absorption line. The emission was stronger in the morning than in the evening, and apparently had a maximum intensity at 70 degrees elongation from the Sun in the ZL. So strong was the emission that it was difficult for these observers to draw any conclusions about the obscured absorption line shape.
In November and December 1967, Reay and Ring repeated their observations from a site at Testa Grigia in the Italian Alps, looking at regions of the sky clear of the ecliptic, in both morning and evening, with an improved instrument. They found more Hp emission, and not only in the plane of the Milky Way. An automatic stepping system and careful calibration were introduced so the identification of the Hp wavelength was now beyond doubt. Even in a moonlit sky (contributing, of course, reflected sunlight with an unshifted Hp line in absorption) the emission was strongly seen. Shifts of the line were observed in some scans in the evening Zodiacal cone – all towards the blue. This was still far from the simple picture of a shifted absorption line which the experimenters had looked for.
This time, however, Reay and Ring attempted to subtract the emission lines from the spectra, to reveal an interpolated absorption feature which hinted at the shifts they were looking for. These correlated tolerably well with a prograde dust model, but the probable errors were high, and the data was confined to evening ZL elongations between 40 and 120 degrees. Nevertheless these data (plotted as green circles in Figure 4.1) stood for some years as the results with which motional models were compared. In their letter to Nature in 1968, Reay and Ring announced their intention to overcome the problems of obscuration of the absorption feature by Hp emission, by switching their attentions to the MgI line at 5183.6 A.
Returning to the absorption line data, Bandermann and Wolstencroft (1969) attempted a better fit to the Reay and Ring data, by basing their model on elliptical dust orbits, rather than circular, but the differences in the predictions were small, and Reay (1969) produced, theoretically, larger variations by including the effects of radiation pressure on orbital speeds. These effects are large in the case of sub-micron particles. Other attempts were made to construct the theoretical shape of an absorption feature from rotating dust-cloud models, notably James (1969).
Vanysek and Harwit (1970) pointed out that the Reay and Ring data were actually not inconsistent with the theory that a ‘Cis-Terrestrial Cloud’ (CTC) was responsible for the ZL, and predicted a drop in the wavelength shift at elongations of about 70 degrees. They also showed that the application of full Mie Theory to the scattering problem produces predictions very similar to the Hulst-Ingham-Reay method of treating reflection and refraction separately (Ingham 1961).
New experimental data was obtained by James and Smeethe (1970), using the new target absorption line, MgI (5183.6 A), who attempted to make observations of the more elusive (because of twilight and atmospheric extinction) lower elongation regions in the both the morning and evening ZL. Their results (shown as brown crosses in Figure 4.1) did show high shifts at low elongations, which is what the circumsolar prograde models predict, but the radial velocities they found looked too large to lie on the p = 5 theoretical curve (see topic 4), and again the probable errors made it impossible to support any firm conclusions. The observations were limited to a very small range of elongations, so no significant curve-fitting could be done to discriminate between models. James and Smeethe concluded that their observations were consistent with a dust distribution model in whichp < 3, and most of the dust was in prograde solar orbits, but the matter remained unproven.
Throughout these studies prior to 1970, it had been hoped th at the radial velocity patterns found would discriminate between dust in prograde and retrograde orbits around the Sun: if the dust were determined to be moving in orbits around the Sun in the same sense as the Earth (‘prograde’), an asteroidal origin would be favoured. In this hypothesis, due to Fesenkov (1958) collisions and/or cosmic ray bombardment within the asteroid belt produce debris, which slowly spirals in towards the Sun. Other authors of the period, notably Whipple, favoured cometary debris as the principal component of Zodiacal Dust, an idea first suggested by Fesenkov in 1914. Since many comets (in fact perhaps a majority of those with long periods) have retrograde orbits, presumably the discovery of any retrograde elements must favour a cometary component. It is interesting that these two opposing views of the origins of interplanetary dust are still hotly defended in 2007 (see topic 4). A Zodiacal Cloud origin coeval with the Earth and other planets was thought by most to be unlikely in 1974, since the gradual collapse of the orbits of small particles, and their probable eventual vaporisation by the Sun (Dobrovolskii and Egibov 1973), over a timescale short relative to the age of the Solar System, requires that the material is continuously replenished. If the source of replenishment of the material is outside the Solar System, we might expect an entirely different pattern of velocities. However, opinions on the relative strengths of the various forces acting on a particle vary greatly, so the question of the age of the Zodiacal Dust may be regarded as still unresolved, and certainly was in 1970. If the dust did turn out to be a remnant of the creation of the Sun’s whole planetary system, we would still expect a predominantly prograde cloud.
To sum up, in 1970, uncertainties in observations of radial velocities, combined with uncertainties as to which theoretical model should be used as a comparison, left the question of the real motions of Zodiacal Dust completely open.
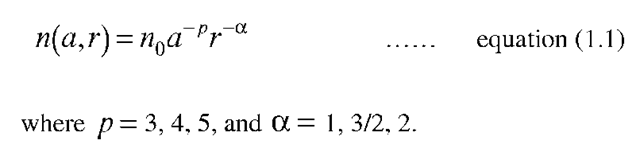
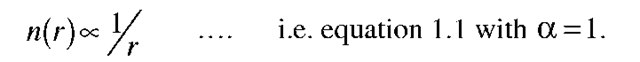
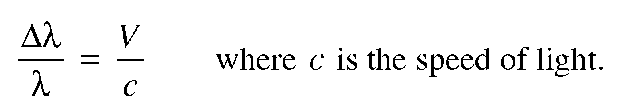
![tmp69-10_thumb[2] tmp69-10_thumb[2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp6910_thumb2_thumb.png)
![tmp69-11_thumb[2] tmp69-11_thumb[2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp6911_thumb2_thumb.png)
![tmp69-13_thumb[2] tmp69-13_thumb[2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp6913_thumb2_thumb.png)
![tmp69-15_thumb[2] tmp69-15_thumb[2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp6915_thumb2_thumb.jpg)