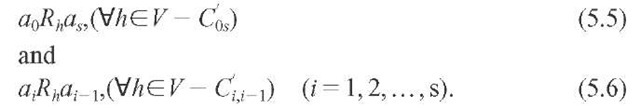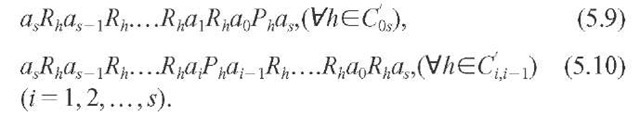5. Negative Externalities and Cyclical Social Preferences
In this Section we prove
Theorem 2. Externalities are a necessary condition for the existence of cyclical social preferences.
Define first negative externalities. Denote by![]() a winning coalition which can decide among outcomes
a winning coalition which can decide among outcomes![]() Note that this can either be a coalition which has the right according to the assignment of rights and the prevailing decision rule to decide among alternatives of one issue, so that the two outcomes are only different in this issue. Or that the winning coalition could come about by a contract among such coalitions who agree on their preferences for the two outcomes which differ in more than one issue. Definition of negative externalities: Assume that a Cj exists for all of whose members
Note that this can either be a coalition which has the right according to the assignment of rights and the prevailing decision rule to decide among alternatives of one issue, so that the two outcomes are only different in this issue. Or that the winning coalition could come about by a contract among such coalitions who agree on their preferences for the two outcomes which differ in more than one issue. Definition of negative externalities: Assume that a Cj exists for all of whose members![]() . In this case we get aiPaj. Thus this winning coalition can bring about the former outcome, whenever the latter is present. Then negative externalities exist for other members of society not belonging to the coalition if
. In this case we get aiPaj. Thus this winning coalition can bring about the former outcome, whenever the latter is present. Then negative externalities exist for other members of society not belonging to the coalition if![]()
This is a very broad definition. Negative externalities include not only the externalities usually considered in economics, but also the negative consequences for the individuals who have the right to participate in a decision, but who are “outvoted” according to the decision rules prevailing in the organisation(s). This latter phenomenon has been mentioned early by Buchanan (1962) and Buchanan and Tullock (1965) as stemming from the fact that collective decision-making not requiring unanimity may lead to negative externalities.
Let us prove now Theorem 2. We take into account that individuals may be indifferent between two outcomes, and denote by![]() that individual h is either indifferent
that individual h is either indifferent
between these two outcomes or prefers the former to the latter outcome. Consider outcomes a0, a^…, as. Assume that cyclical social preferences exist:![]()
Then there exist winning coalitions ![]() for whom
for whom![]()
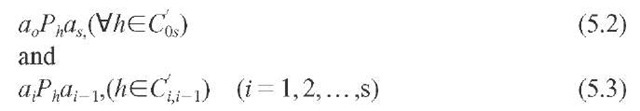
is valid.
(5.1) implies, because of the transitivity of individual preferences:
which implies the absence of dictatorship.
We assume now that no negative externalities exist for the members of society not belonging to the above winning coalitions, and show that this leads to a contradiction. It follows from the absence of negative externalities that
From (5.2) and (5.5) and from (5.3) and (5.6), respectively,
whose members (5.3) or (5.2) is valid. Since![]()
(5.7) and (5.8) are true for all of their members. But then one can derive from (5.2) and (5.8) or from (5.3), (5.7) and (5.8), respectively:
This result, however, contradicts the assumption of transitive individual preferences. Thus, cyclical social preferences can only exist if negative externalities are present.
Theorem 2 has far-reaching consequences. It suggests that the assignment of rights is of decisive importance for the occurrence of cyclical social preferences. Even more, according to the Coase Theorem the original assignment of rights is not important if no transaction costs for concluding contracts are present, since then all negative externalities can be removed by mutually beneficial agreements. Before returning to this problem in section 7, however, let us take up the influence of the kind of assignment of rights.
6. Cyclical Social Preferences and Assignment of Rights
Denote by a profile of individual preference orderings a m-tuple of individual preference orderings, one for each of the m members of society. Obviously there exists a huge number of such profiles, since people can have many different preference orderings. Subsequently we illustrate with the help of examples (for a general proof see Bernholz, 1986).
Theorem 3. For each possible profile of individual preference orderings, there exists a non-oligarchic assignment of rights to decide among all pairs of outcomes, such that no intransitive social preferences exist, and that a stable Pareto optimal outcome results.
Note that rights are referred to in the theorem as rights to decide among pairs of outcomes instead of among alternatives of issues. This is, however, not important. For if we add to the right to decide issues the right to conclude contracts, both rights together imply a right to decide among certain pairs of outcomes for the winning coalitions agreeing on the respective contract.
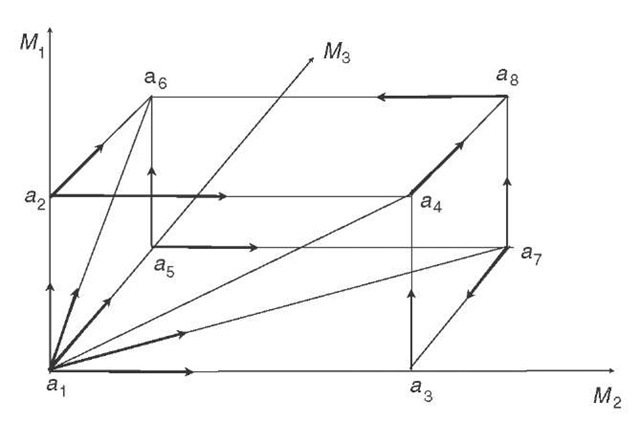
Consider first the examples of Table 1 and of Figures 2 and 3. In these cases the same individual preference
Figure 5: Reassignment of rights to decide issues prevents cyclical social preferences.
orderings lead through two different assignment of rights and the conclusion of contracts to cyclical social preferences. According to Theorem 3 there should, however, given the profile of individual preferences, exist an assignment of rights preventing cyclical social preferences. And this is indeed the case for the following assignment:![]() ,
,
![]() The resulting situation is presented in Figure 5 in which no cycles exist and in which a1 is the stable, Pareto optimal outcome. The diagonal from
The resulting situation is presented in Figure 5 in which no cycles exist and in which a1 is the stable, Pareto optimal outcome. The diagonal from![]() shows no arrow, since the preferences of the potential partners are opposed, so that no contract is concluded. For all other diagonals the same is true or the potential contracts do not imply cyclical social preferences. Moreover, they would not be concluded since they would not lead for the participants of such contracts to a better or another outcome than a1.
shows no arrow, since the preferences of the potential partners are opposed, so that no contract is concluded. For all other diagonals the same is true or the potential contracts do not imply cyclical social preferences. Moreover, they would not be concluded since they would not lead for the participants of such contracts to a better or another outcome than a1.
Moreover, when analysing whether there exists an assignment of rights preventing cyclical social preferences in the example of Figure 4, we find that the assignment just given, and thus the situation depicted in Figure 5, is again a solution. This is not surprising, for the preferences of the three members of society are the same as in Table 1, except that for individual 1![]() instead of the opposite preference among these outcomes. But 1 has no right to participate in the decision concerning issue M3, so that the situation of Figure 2 remains unchanged. It is important to point out, that within the framework of total direct democracy present in the logrolling case, no solution can be found for removing cyclical social preferences, except with unanimity as a voting rule, whereas an individualistic liberal reassignment of rights offers a solution. This is not the accidental result of our specific example, since it has been shown (Bernholz, 1986: 256f.) that:
instead of the opposite preference among these outcomes. But 1 has no right to participate in the decision concerning issue M3, so that the situation of Figure 2 remains unchanged. It is important to point out, that within the framework of total direct democracy present in the logrolling case, no solution can be found for removing cyclical social preferences, except with unanimity as a voting rule, whereas an individualistic liberal reassignment of rights offers a solution. This is not the accidental result of our specific example, since it has been shown (Bernholz, 1986: 256f.) that:
Theorem 4. For any possible profile of individual preferences there exists a purely liberal assignment of the rights to decide among all pairs of outcomes, such that no intransitive or cyclical social preferences exist and that any outcome to which no other outcome is preferred is Pareto optimal. But the same result does not hold if we assign the rights to decide among all pairs of outcomes to all members of society (Total Direct Democracy), deciding with simple or qualified majorities.
Since the general approach presented here does include pure individualistic liberalism, it also covers Sen’s (1970) well-known example concerning the conflict between mother and daughter whether they should read Lady Chatterley’s Lover. Decision rights for the two issues are only assigned to individuals, namely mother and daughter. It will be shown that in this example, too, negative externalities are present, that the conclusion of a contract leads to cyclical group preferences, and that they can be removed by a different assignment of rights. Following Sen, let us assume![]() and
and![]() , where 1 denotes
, where 1 denotes
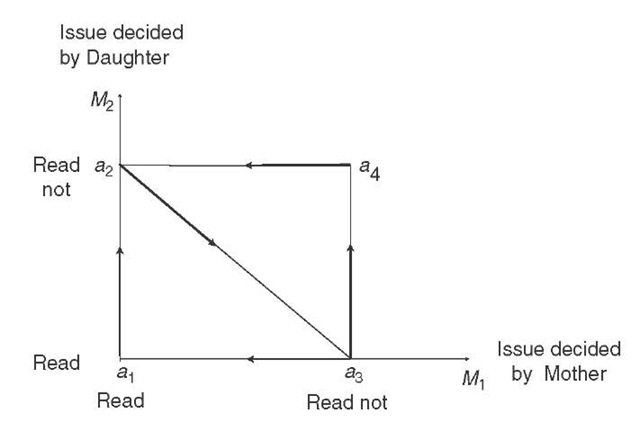
the mother and 2 the daughter. The two issues M1 and M2 refer to reading the book by mother and daughter, respectively. The two alternatives of each issue are “reading” and “not reading” by mother and daughter. Table 2 describes the strong preference orderings of mother and daughter over the four outcomes. As can be seen, the decisions by the mother lead to negative externalities for the daughter, and vice versa.
The resulting situation is sketched in Figure 6. The stable outcome without contract, a3, is Pareto-inferior. This is Sen’s celebrated theorem of the Impossibility of a Paretian Liberal. But if we allow a contract between mother and daughter, such an outcome will be agreed on, since both prefer a2 to a3. But the contract implies a social preference cycle, because the mother prefers a1 (both do not read), and the daughter a4 (both read the book) (Theorem 1). But a stable outcome is reached without a contract if the right to decide M1 is assigned to the daughter and that to decide M2 to the mother (Theorems 3 and 4).
Table 2: Preferences for reading Lady Chatterly’s Lover
| Members of society | ||
| Mother 1 | Daughter 2 | |
| Strong | ![tmp16E-179_thumb[1] tmp16E-179_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/04/tmp16E179_thumb1.jpg) |
![tmp16E-180_thumb[1] tmp16E-180_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/04/tmp16E180_thumb1.jpg) |
| Separable | ![tmp16E-181_thumb[1] tmp16E-181_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/04/tmp16E181_thumb1.jpg) |
![tmp16E-182_thumb[1] tmp16E-182_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/04/tmp16E182_thumb1.jpg) |
| Individual | ![tmp16E-183_thumb[1] tmp16E-183_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/04/tmp16E183_thumb1.jpg) |
![tmp16E-184_thumb[1] tmp16E-184_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/04/tmp16E184_thumb1.jpg) |
| Preference | ![tmp16E-185_thumb[1] tmp16E-185_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/04/tmp16E185_thumb1.jpg) |
![tmp16E-186_thumb[1] tmp16E-186_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/04/tmp16E186_thumb1.jpg) |
| Orderings | ||
Figure 6: Reading Lady Chatterly’s Lover.
It has been pointed out correctly that the results presented by Theorems 3 and 4 may be interesting logically, but that their relevance for reality is rather limited, since an assignment preventing cyclical social preferences would have to be based on a knowledge of all individual preference orderings in society. As a consequence, one has to ask whether the same or a similar result cannot be reached by individual decisions, given some original assignment of rights. This is, indeed, the case, as will be shown in the next section.
7. Cyclical Social Preferences, Negative Externalities and the Coase Theorem
Negative externalities are a precondition for the existence of cyclical social preferences. But then the possibility to conclude contracts should, according to the Coase Theorem (Coase, 1960), lead to stable Pareto optimal outcomes, whatever the original assignment of rights, provided that there are no transaction costs. And social choice theory as well as the theory of logrolling do not assume the presence of such costs. It seems to follow that the Coase Theorem contradicts Theorem 1, which asserts that contracts are a major reason of cyclical social preferences.
But this seeming contradiction can be removed, if contracts are binding, and if the Coase Theorem is generalised. Subsequently, a difference will be made between internal and external contracts. An external contract is a contract agreed on by organisations or individuals with other organisations or individuals. An internal contract, by contrast, is a contract concluded by the members of a winning coalition who have the right to decide an issue for an organisation according to its decision rule, to bring about a certain alternative. Note that this may but need not be done by agreeing to an external contract.
Let us now illustrate with several examples that the generalised Coase Theorem holds if internal as well external contracts are binding. Consider first the example of Table 2 and Figure 6. In this case only external contracts can be concluded, since no organisation is present. The contract to bring about a2 is advantageous to both mother and daughter. If it is also binding, then this Pareto optimal outcome is also stable. For outcomes a1, a4 and thus cyclical social preferences could only come about, if mother or daughter, respectively could break the contract. This result demonstrates also that Sen’s theorem of the Impossibility of a Paretian Liberal, though true, is based on a too narrow conception of liberalism. For if the possibility of binding contracts is included, the supposed paradox disappears.
Consider next the logrolling example of Table 1 and Figure 3. In this case only internal contracts can be agreed on by winning coalitions, since![]() 1 and 2, for whom
1 and 2, for whom![]() are minorities if issues M1, M2 are voted on separately. They thus have to conclude a contract to bring about a winning logrolling coalition for outcome a1. But since 2 prefers a2 it is motivated to b break this internal contract. This is, however, prevented if the contract is binding, and no cyclical social preferences result. Note also, that the resulting outcome is Pareto optimal. The same analysis is valid for the example of Figure 4.
are minorities if issues M1, M2 are voted on separately. They thus have to conclude a contract to bring about a winning logrolling coalition for outcome a1. But since 2 prefers a2 it is motivated to b break this internal contract. This is, however, prevented if the contract is binding, and no cyclical social preferences result. Note also, that the resulting outcome is Pareto optimal. The same analysis is valid for the example of Figure 4.
Things are a little bit more complicated for the example of Table 1 and Figure 2. In this case only![]() whereas
whereas
![]() . As a consequence an external and an internal contract are involved in bringing about a1 instead of a4. An external contract concluded between V1 and V2; and an internal contract between 1 and 2to vote for the respective alternative of M2, though for
. As a consequence an external and an internal contract are involved in bringing about a1 instead of a4. An external contract concluded between V1 and V2; and an internal contract between 1 and 2to vote for the respective alternative of M2, though for![]() But a1 is not stable,
But a1 is not stable,
even if both contracts are binding. For 3 has the right to decide M3 and prefers a5. Obviously, Pareto optimal outcome a4 is a candidate for an external contract by all Vi and an internal contract by 1, 2 and 3 to vote for the respective alternative of issue M2. Note that in this case all participants to the contract have an incentive to break it. 3 prefers a8 and has the right to bring it about. 1 and 2 would prefer to move to a1 and could do it by the contract described above. This would imply that 1 would break the external contract for V1, and that both would break the internal contract on how to vote on issue M2, which would also violate the external contract concluded for V2. But again, if both external and internal contracts are binding, stable Pareto optimal outcome a4 comes about.
The results just discussed suggest (for a general proof see Bernholz, 1997, 1999).
Theorem 5. Assume that weak, ordinal, complete and transitive individual preference orderings are present, that at least one finely divisible good exists, that any decentralised original assignment of rights to subsets of society is given to decide issues, and that no cyclical social preferences are present without contracts. Then if binding external and internal contracts can be concluded, a stable Pareto optimal outcome results from the decisions of the members of society.
8. Conclusions
The conclusions drawn above underline first the importance of a clear and complete assignment of rights to decide issues, that is also of property rights. They show second the importance of the freedom to conclude binding contracts, and stress third the need for a legal system trying to prevent any violation of contracts by sufficiently strong sanctions. The results, therefore, cast doubt on the social opprobrium against concluding contracts concerning political decisions, and the absence of fines and penalties if such contracts are broken. Even the prohibition to exchange or sell votes seems to be problematic. The possibility to enforce “political” contracts under certain conditions within the framework of repeated games may not be sufficient to overcome the implied disadvantages in many empirical cases. Finally, the meta-rights of some organisations like parliament, government or bureaucracy to reassign decision rights more or less at their discretion, may have severe negative consequences for society. On the other hand, new issues and alternatives are coming up all the time, so that some organisation is needed to assign them. Connected to this may be a necessity to reassign some rights concerning the old issues. But much work remains to be done to clarify these problems.
Moreover, great caution is advisable concerning the interpretation of the conclusions. First, no strategically motivated decisions to bring about a preferred outcome were taken into account. Second, the absence of transaction costs has been assumed. This is a severe restriction, since binding contracts implying up to n issues may be needed to bring about the stable Pareto optimal outcomes. And transaction costs will generally increase with the number of issues and people involved. As a consequence, many binding contracts may not be concluded because of such costs. Note also that the presence of transaction costs may be a sufficient condition for the evolution of organisations in history. For we have shown that up to n-issue contracts may be necessary to get stable Pareto-optimal outcomes. But if transaction costs are no longer neglected, it is clear that they generally increase with the number of issues and of people involved. It follows that this is already a sufficient condition for the evolution of organisations in history, of organisations which control one or more issues, so that the number of people participating in negotiating contracts and thus contract costs are reduced. From this conclusion it follows that it is not possible to agree with Williamson’s statement (1981: 1545): “that but for the simultaneous existence of bounded rationality and opportunism, all economic contracting problems are trivial and the study of economic institutions is unimportant. Thus, but for bounded rationality, all economic exchange could be effectively organized by contract.”