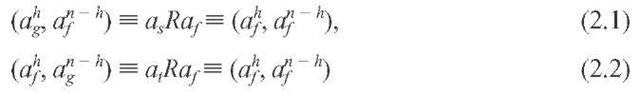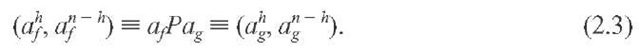The problems connected with logrolling (Bernholz, 1974) and vote-trading (Kramer, 1973; McKelvey, 1976; Plott, 1967) are special cases of much wider phenomena (Bernholz, 1981; Schwartz, 1981, 1986). These phenomena are in fact the only reason for the inconsistencies of non-dictatorial societies described by Arrow’s General Impossibility Theorem (Arrow, 1963/51; see Sen, 1987, for a review of Social Choice Theory) if more than one issues are implied, if individuals have separable preference order-ings and if such inconsistencies are not present concerning the alternatives of single issues. Moreover, the respective "paradoxes" of voting and logrolling, usually distinguished in the literature, are identical (Bernholz, 2000). Also, the implied social inconsistencies can even occur if participating individuals have identical preferences but face different restrictions (Breyer, 1980). Finally, the problems put into the centre of attention by Arrow would not exist without the presence of negative externalities (in its broad sense, that is including also political externalities). But then, as suggested by the Coase Theorem, stable Pareto-optimal outcomes do result in the absence of transaction costs in spite of the validity of Arrow’s Theorem, provided that binding contracts are possible. Consequently, the following statement by Sen (1987: 383) is only true if contracts are not binding: "…it would appear that there is no way of arriving at a social choice procedure specifying what is to be chosen., satisfying the appropriately interpreted (i.e., in terms of choice) conditions specified by Arrow.."
1. Definitions and Assumptions
To consider the general nature of the phenomena, consider a decentralised society, in which
is the set of issues among whose alternatives humans can select. Each issue comprises at least two alternatives
An outcome is defined as containing one alternative out of each issue:
Consequently,
where
Further, let
denote the n sub
sets of society to which the rights to decide the n issues Mi have been assigned. V is the set of all adult people in society. We assume, that these m individuals have weak, ordinal, complete and transitive preferences over all outcomes. In some cases we will assume that individual preference orderings are separable. This means that if an individual prefers alternatives of one or a number of issues to other alternatives of the same issue(s), where the alternatives of all other issues remain constant, then this is also true for different alternatives of the other issues held constant. Formally, consider four different vectors
such that
The four vectors contain h and n-h different alternatives, respectively, one out of each issue. Denote by Rj that individual j either prefers the first alternative to the second or is indifferent among them. Assume that 
Then individual preferences are separable if also
holds. Or, similarly, if
then
is valid.
Return to the decision-making subsets of society. If 
we call this an organisation. An organisation is supposed to have any consistent decision rule like simple majority voting, voting with the majority of stocks, or unanimous decision-making to decide among alternatives. Moreover, let 
be the "winning coalitions" of the organisation, that is the subset of people who, according to its decision rule, can take decisions for the organisation. Only one such coalition exists, namely
if unanimity is required. This is also the case, if Vi contains only one individual. Finally, dictatorshipis excluded by assuming that there exists no individual
for which
for all i.
These definitions and notations comprise a very broad range of institutional settings. For instance, if
for all i, and if simple majority voting is used throughout, we may speak of a Total Direct Democracy. For in this case all issues are collectively decided by all citizens by applying simple majority voting. On the other hand, if 
and if each individual j has assigned the right to decide at least one issue, one may call this Pure Individualistic Liberalism. Another form of Pure Liberalism would be present, if
for all i,
if
and if each individual
belonged to at least one Vi.
2. Logrolling and Cyclical Social Preferences
We prove first that a logrolling agreement beneficial to its participants implies always cyclical social preferences. It is assumed that individuals have complete, weak, transitive and separable individual preference orderings (the separability assumption makes the proof easier, but it can be removed, see below). A logrolling situation is given if all decisions are taken by majority (or qualified majority) voting of the members of a group; if two or more subsets of this group who prefer intensively certain alternatives of different issues to others would remain in a minority concerning their favoured issues, but could form a majority by agreeing to vote for each other’s alternatives in an exchange of votes. This exchange of votes for the alternatives of different issues implies, however, that the decision in favour of the unwanted alternatives of other issues is not as important as that relating to the alternatives of the issues favoured by the members of the own subset of the group. This means that to assume separable individual preferences is adequate in such a situation. Subsequently only an agreement among two subsets of society will be analysed, but an extension to the case in which more than two subsets have to join to win a majority is straightforward.
Formally, assume that
where R means "the group prefers or is indifferent to". Note that "group indifference" can not only arise because all group members are indifferent among the respective outcomes, but also since no majority can be found for one of the two outcomes. This is especially possible if a qualified majority is required by the decision rule.
Now assume further that
Then a logrolling situation allowing a successful agreement among a majority is present. For the last assumption means that a majority (or a qualified majority) of individuals in the group prefers
But this implies together with the first two assumptions and the assumption of separable individual preferences that this majority is composed out of two subsets of the group who form each a minority and for whose members
respectively.
The existence of cyclical social preferences can now be derived easily. For first, from (2.1) and (2.2) respectively,we get by using the assumption of separable individual preference orderings:
And second, it follows from (2.3) together with (2.5) and (2.1), and with (2.4) and (2.2):
and
It is important to realise that the preferred, but dominated and consequently unstable outcome af can be reached in two different ways by the winning coalition composed out of the two subsets of society. First, with ag being the status quo, the coalition can first vote on this outcome as compared to as or at in favour of one of the latter, and then in favour of af compared to these outcomes. This will be called explicit logrolling in contrast to implicit logrolling. Implicit logrolling takes place if the coalition votes directly in favour of af put against the status quo ag. This presupposes that the changes in the alternatives of the issues at stake can be bundled together by the coalition into one bill. The different problems connected with implicit and explicit logrolling will be taken up in the next section.
3. Logrolling by Majorities and the Paradox of Voting
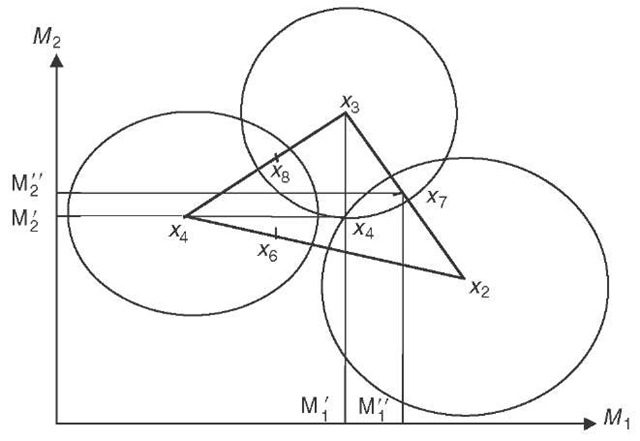
Let us turn next to prove the identity of logrolling and the paradox of voting, assuming that two or more issues are present. Consider the graphical representation in Figure 1. Two issues M1 and M2 with infinitely many alternatives are assumed. Society comprises only three members as voters. Also let
, i.e., all members of society have the right to decide the two issues. As a decision rule simple majority rule is assumed for both issues. The most preferred outcomes for voters 1, 2 and 3 are
respectively. The circles or ellipses around these points combine all outcomes for which the voter in question is indifferent. The further away such a curve from the most preferred outcome the less the outcomes on it are estimated by the voter.
This implies that all three voters have single-peaked preferences. But it is well-known that this is not a condition sufficient to secure a stable outcome if simple (and in this case even two-thirds) majority voting is used . True, if voting would take place independently on the two issues, 
, which combines the two most preferred positions of the two different median voters, would be selected. But voters 2 and 3 prefer x7 to this outcome, so
that it will receive a majority if put to a vote against x4. But the former is itself dominated by x8, which is preferred by 1 and 3. Similarly, x8 is dominated by x6, itself dominated by x4. Thus a cycle exists and no outcome is stable. It is easy to show that this is just one of infinitely many possible cycles, that the outcome may wander anywhere (McKelvey, 1976), and also, that the conditions for a stable outcome are very restrictive (Plott, 1967; Kramer, 1973).
Figure 1: Logrolling and the paradox of voting.
Note next that by moving from one outcome to another, the respective majority is creating in each case a negative externality to the outvoted voter (minority). Thus, as will be proved in Section 4, negative externalities are here as always a precondition for a cycle. Moreover, the majorities in question have to follow an agreement as to their voting behaviour. This can be done in two ways: Either, an explicit logrolling contract is concluded for instance by 2 and 3 to bring about x7 instead of x4: Both agree to vote first for M" of the first, and then for M2" of the second issue. In this case voting on the two issues takes place separately.
Or the two issues are bundled together (e.g., in one bill), so that only one vote takes place between x4 and x7, where x7
= {M", M2"}. This is a contract which Gordon Tullock has 
named implicit logrolling. Explicit logrolling is problematic, since 2 would prefer not to keep his part of the bargain in the second vote and vote for M2′. But even if x7 is brought about (as is certainly the case if implicit logrolling is used), it is still unstable. For other contracts are better for different majorities, so that further logrolling agreements are favourable, which leads to cyclical social preferences. Thus logrolling contracts are a precondition for cyclical preferences. Moreover, it follows from the example, given the case of implicit logrolling, that the paradox of voting for two or more issues is identical to the fact that majority logrolling is possible.
With many voters present it will usually not be possible for them to conclude logrolling agreements. But in this case parties may exist which propose packages in their election platforms containing alternatives of several issues. If such a package is beneficial to a majority of voters, we have again a case of implicit logrolling, but with the contract now proposed by outsiders, the parties. As a consequence, cyclical social preferences are present again. And this means that any party program proposed by one party can be defeated by that of another party, as already recognised by Downs (1957: 55-60).
4. The General Relationship between Contracting and Cyclical Social Preferences
It has already been stated that logrolling is just a special case of a much more general phenomenon, which has now to be analysed. Assume that all individuals have separable individual preference orderings, and that no cyclical social preferences exist concerning single issues. That is, there is no collection of at least three different winning coalitions 
, such that for outcomes different only in alternatives of issue i:
is valid. Recall that P means "preferred by society", and R that "society" either "prefers" an outcome to the following one or is "indifferent" between them. Note again that the latter can also occur when no winning coalition exists for one of the two outcomes following each other in the sequence.
Given these assumptions, it follows that cyclical social preferences can only occur, if two or more winning coalitions exist, which may be called without loss of generality 
who have the right by using their respective decision rules to decide different issues
and who agree to bring about an outcome preferred to the status quo by all of their members. This means that only by agreeing on such an outcome, that is by concluding a contract, cyclical social preferences arise.
This result holds for the following reasons. First, given separable individual preferences, it follows from the absence of cyclical social preferences in single issues, that such cycles can also not occur if only the alternatives of other issues are different. For since this does not influence the preferences of the members of the winning coalitions concerning their issues because of the assumption of separable individual preferences, this is also true for their decisions and consequently for the "preferences of society". Second, none of the winning coalitions can bring about the new desired outcome on its own, since it does not control the other issues, for which it is not a winning coalition. Otherwise the outcome would already have resulted before. Consequently, if cyclical social preferences occur they can only result from contracts referring to more than one issues controlled by the winning coalitions to bring about preferred outcomes.
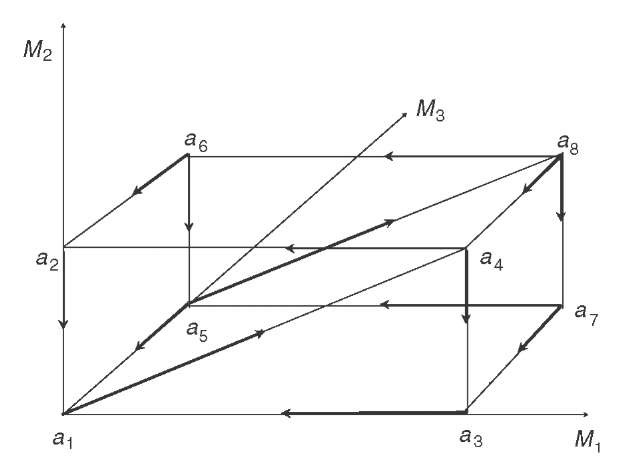
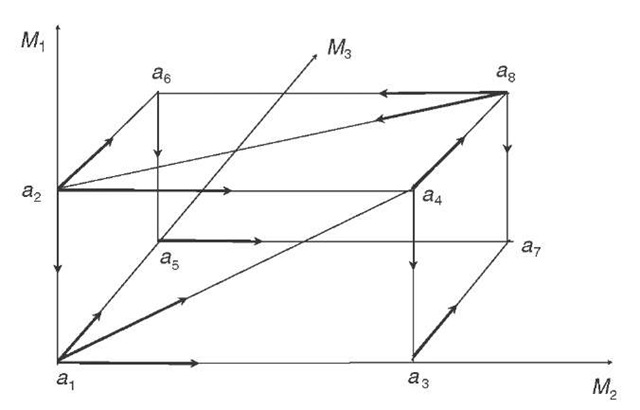
Let us illustrate this result with the help of an example. Assume three issues, each with two alternatives, and a society comprising three individuals, i.e.,
. The number of outcomes is, therefore, eight. Moreover, we assume strong individual preference orderings (i.e., individuals are not indifferent among any pair of outcomes), and for individuals 1 and 3 separable individual preference orderings concerning issues M1 and M3, respectively, and for all individuals concerning issue M2 (Table 1).
The right to decide issues one and three is assigned to individuals one and three, respectively. All members of society have the right to decide issue two by simple majority vote. Thus we assume
{1,2,3}. The resulting situation is sketched in Figure 2. Here the arrows point from the outcomes preferred by society to those dominated by them. For instance for individual 1, who has the right to decide the first issue,
, so that "society" also "selects" the former outcome. Concerning the second issue,
so that the former is chosen by majority voting. Note also, that all parallel arrows point into the same direction because of the separable preferences of individuals 1 and 3 concerning issues M1 and M2, and of all individuals concerning issue M2, respectively.
Table 1: Preference orderings of the members of society
|
Individual |
 |
 |
 |
 |
 |
 |
|
|
Strong individual |
 |
 |
 |
|
Preference |
 |
 |
 |
|
Orderings over |
 |
 |
 |
|
Outcomes |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
Figure 2: Contracting as causing cyclical social preferences.
Now without any contracts among different winning coalitions controlling different issues no cyclical social preferences are present and a8 is the resulting stable outcome. But
Note that 1 has the right to decide the first issue, and that 1 and 2 form a winning coalition for the second issue. As a consequence they can conclude an agreement to bring about a5, which is, however, dominated by
which are dominated by a8. Thus cyclical social preferences are caused by the possibility to conclude a contract beneficial for its participants.
It remains to prove that cyclical social preferences will always result, whenever a contract between winning coalitions controlling different issues benefits all of their members. This is easy to prove. Without contracts and no cyclical social preferences among the alternatives of single issues there can also be no cyclical social preferences comprising alternatives of two or more issues. This follows from the separability of individual preferences, which implies that the decision by those controlling an issue will remain the same whatever decisions others take concerning the other issues they have the right to decide. This implies that in Figure 2 all parallel arrows point into the same direction. As a consequence a stable outcome results. But the conclusion of a contract changes this situation, since it leads to another outcome which is not stable relative to the decisions taken by the winning coalitions controlling individual issues. Otherwise it would have been selected before. Thus the decisions taken independently by these winning coalitions lead back to the originally stable outcome, which is itself dominated by that selected through the contract.
The situation is different and more complicated if non-separable individual preference orderings are present. This is the case for the preference orderings of individual 1 concerning issue M3 in the above example (Table 1), for though
we see that
Similarly, inseparability of preference ordering concerning M1 holds for individual 3. These inseparable preferences were unimportant for the relationships sketched in Figure 2 since 1 and 3 had only the right to decide M1, M3, respectively. But this is no longer the case if a different assignment of rights is considered. As an example, andto bring logrolling into the discussion, assume that 
and that all issues are decided by majority voting. Then the situation of Figure 3 emerges for society.
As can be seen there exist now cyclical social preferences, namely
without any contracts and this means, in this case, without a logrolling agreement being concluded among different winning coalitions controlling different issues. This is a consequence of the fact that the non-separable preferences of individuals 1 and 3 are now decisive concerning M1.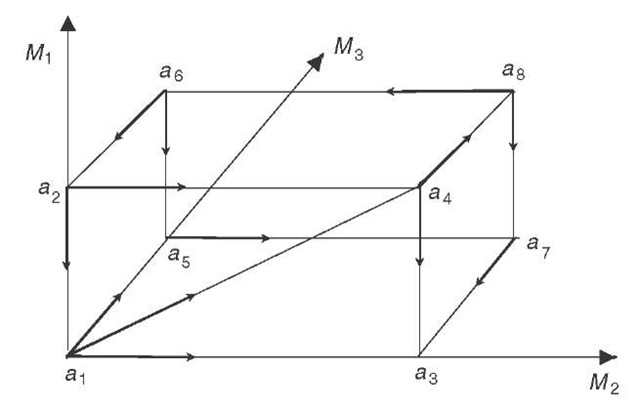
Figure 3: Non-separable individual preferences and cyclical social preferences.
Figure 4: Non-separable individual preferences and cyclical social preferences: Case 2.
But note also that if a contract, in this case a logrolling agreement, is concluded between 1 and 2 to bring about a1Pa4, since they both have corresponding preferences and form together a majority, then an additional social preference cycle is created.
Consider next a third example, in which the preference ordering of individual 1 is changed concerning one pair of outcomes only, namely from
Moreover,
whereas it is assumed as before that
,
with majority voting as a decision rule, the right to decide M3 is now assigned to individual 1,
. Note thatinseparable individual preference orderings are still present. In this example we get the situation of Figure 4.
It follows that no cyclical social preferences are present if no contracts are concluded and that a2 is the only stable outcome. Now let us check whether contracting leads again to cyclical social preferences. This would be not the case, if 1 and 2 would conclude a contract implying
which they could do since they enjoy a majority for both issues M1 and M2. But such a contract would never be agreed on by 2, since the present stable outcome a2 is preferred by it to a1. This is different for a contract between 1 and 3 implying
since they both prefer the former outcome to the latter. Moreover, 1 has the right to decide M3 and they both form a majority for a decision on M1. And this contract leads again to cyclical social preferences. We conclude from this example that contracts bring only about cyclical social preferences if another outcome is "socially preferred" to an outcome which directly or indirectly dominates all other outcomes if no contracts are concluded. However, returning to the second example, this conclusion has to be changed somewhat. For in this example outcomes
are members of a cycle, but dominate
directly of indirectly all other outcomes if no contracts take place. And again, since
, one of this set of dominant outcomes is dominated itself if a contract is concluded. And as a consequence a cyclical social preference cycle results.
The results derived with the help of the examples allow to formulate
Theorem 1. Assume weak, ordinal, complete and transitive individual preferences and a society in which there exists a decentralised assignment of the rights to decide issues, together with appropriate decision rules for organisations. Then, if no cyclical social preferences are present without contracts being concluded on decision-making concerning different issues, then each conclusion of such contracts leads to cyclical social preferences. Moreover, if a subset of outcomes exists for which cyclical social preferences are present if no contracts are concluded, and which dominate directly and indirectly all other outcomes, then additional cycles result if contracts are concluded by which one of the latter outcomes dominates one of the former (for general formal proofs see Bernholz, 1980; Schwartz, 1981, 1985).
Note that the special case of separable individual preferences is covered by Theorem 1. For in this case one stable dominating outcome exists without contracts, if no cyclical social preferences exist among outcomes different only in single issues. It then follows from the Theorem that the conclusion of contracts is the only reason for the emergence of cyclical social preferences.
