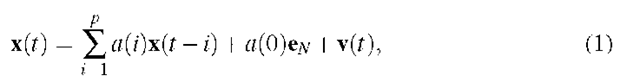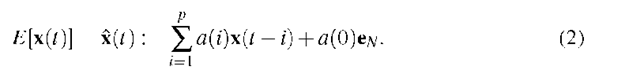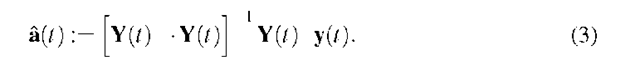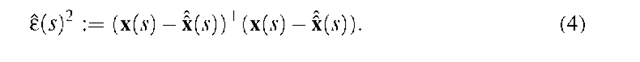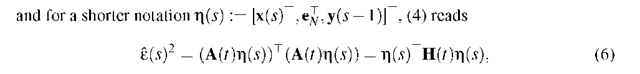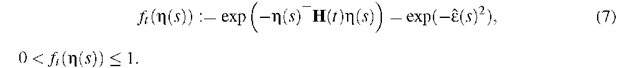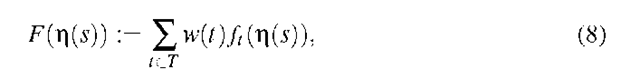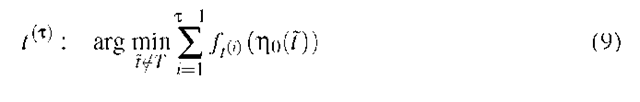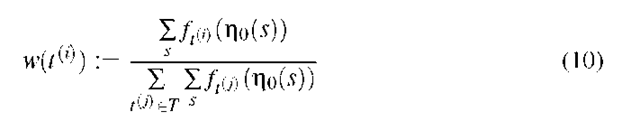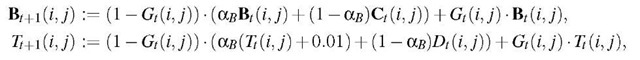Abstract
In this paper, we propose a method for the detection of irregularities in time series, based on linear prediction. We demonstrate how we can estimate the linear predictor by solving the Yule Walker equations, and how we can combine several predictors in a simple mixture model. In several tests, we compare our model to a Gaussian mixture and a hidden Markov model approach. We successfully apply our method to event detection in a video sequence.
Introduction
Event detection [2,4,11] is one of the basic tasks for automatic surveillance. Suppose we observe a complex machinery using several sensors, and we want to distinguish between normal activities and a malfunction (event). As failures are rare occurrences and their properties are commonly unknown, it is difficult to model the malfunctions in a direct manner. To circumvent this problem, we can create a model that describes the machinery when it works normal, and define the "events" as the absence of the "normal case". Our goal is to determine a simple but effective method for this distinction.
An usual approach is to predict the next observation using the knowledge of several previous ones, measure the true observation afterwards, and compare the prediction with the true observation [3,1]. If the difference is higher than a given threshold, we decide "event". Using linear functions for the prediction [8,5] provides several benefits, in particular the ease with which the parameters are estimated.
Two of the most commonly used models for event detection are Gaussian Mixture Models (GMMs) [11] and Hidden Markov Models (HMMs) [4]. While GMMs ignore any temporal connection between samples of the observed stochastic process, HMMs include some temporal coherence. Our approach has several similarities with the GMMs and HMMs. While GMMs use the location in a feature space to distinguish the "normal case" from the "events", our method uses a multiple filter approach [3], respecting a temporal connection between measurements. In comparison to HMMs, our method is simpler to implement, and we use the temporal connection directly, not over the abstract concept of hidden states.
Assuming the input signal is not stationary, adaptive filters like Kalman filters [3] are needed. However, linear adaptive filters include several strong assumptions with respect to the observed data, like Gaussianity and linearity. As a bridge gap solution, linearity is assumed over short intervals. This leads to methods like the extended Kalman filter [3]. We propose here an alternative, in the form of a mixture of linear one step predictors.
Our method has several advantages, for example less training vectors are needed to achieve comparable results. Furthermore, for event detection, should what we define as the normal case change with time, our method can be easily adapted.
The rest of this paper is structured as follows. In Section 2, we estimate the parameters of a linear prediction, and demonstrate how we can apply a mixture of such predictors to event detection. In Section 3, we demonstrate the effectiveness of the model we propose here in several experiments. In Section 4 we present our conclusions.
Linear Predictor Mixtures
The parameters of one step linear predictors (see Section 2.1) are computed from the Yule-Walker-equations [9,10]. In Section 2.2, we show how we can build a mixture of several predictors to describe more complex data.
Linear Predictors and Linear Prediction Error Filters
There is a strong relationship between Linear Predictors (LPs) and Autoregressive (AR) models [1]. Let x be a sequence of observations, x(t) e RN, we assume that x(t) is a linear combination of its p predecessors x(t – p),…,x(t – 1), a constant term and an error term
Using the assumption that the errors v are mutually independent Gaussian distributed, we can estimate the linear predictor [1,9,10] by
The quadratic prediction error at time step s is e(s)2 := (x(s) – x(s))T(x(s) – x(s)). If we use the estimated predictor a(t), we obtain in (2) the estimation of x(s), that is x(s) := X(s) • a(t), and we estimate the prediction error by
This error is most important for the event detection, because if the prediction error is high, we have observed an event.
Using a matrix representation of the linear predictor
with H(t) := A(t)TA(t). This becomes useful for the Linear Predictor Mixture model (LPM) we describe in the next section.
Mixture Model and Detection of Events
In order to create a LPM, we use the exponential representation of the error
The LPM has similarities to Gaussian Mixture Models (GMMs) [11]. Let gi(x) be an Gaussian distribution, than the GMM p(x) = ZieIw(i)gi(x) is an approximation to a more complex distribution; I is a set of indices, and w(i) are weights with "LieIw(i) = 1, w(i) > 0. In the same manner, the LPM is a mixture of several linear prediction error filters (see Equation (5)), and therefore an approximation to complex time series that are not stationary. We use the exponential representation (7) in a weighted sum, similar to GMMs:
T is a set of time indices that refers to a training dataset. Note that F is not a probability function, because we use no normalization of the exponential functions. Hence, we refer to F by score in the following. Similar to GMMs, an event is detected if the score is below a threshold 9 with 0 < 9 < 1.
Parameter Estimation
The parameter estimation for our model proceeds in two steps: first, we estimate a set of several linear predictors a(t), second, we estimate the weights w(t).
Let x0 be a training set of observations. We initialize the index set T with one time index t(1): T ^ {t(1)}. Note that with t(1) and (3), a unique estimated linear predictor a(t(1)) is defined.
At iteration t > 1, we want to add an estimated linear predictor a(t (t)) that reduces the highest prediction error of the training dataset. Hence, we set
and
is the combination of several observation vectors similar to n in Section 2.1 and 2.2, with respect to x0. We terminate this parameter estimation stage if we have a fixed number Tmax of predictors. The weights in Equation (8) are computed by
for each
The estimated linear predictors and the weights define the LPM, see
Equation (8). In the next section, we will test this model in comparison to GMMs and HMMs.
Experiments and Discussion
Our experiments consist of two parts: in the first part, we use simulated data and compare the LPM with a GMM and an HMM. In the second part, we use a LPM to detect events in a video stream.
Comparison to GMMs and HMMs on Synthetic Data
In this test, we compare the LPM with two of the most commonly used models for event detection, the GMM and the HMM. This test is designed as a proof of concept; we concentrate on a real problem in the next section, in this one, we use synthetic data, which has the benefit that we have enough data for each model. A problem with insufficient data especially arises with the HMM, because to estimate the transition probabilities, we need to observe enough transitions.
3.1.a Synthetic data. Similar to HMMs, the model we use as a generator for the synthetic data consists of five states, and it switches between the states at random. As a difference to HMMs as they are discussed in [7], each state in our model is associated with a linear filter, not with a distribution, in order to create a more sophisticated temporal connection. In detail, the synthetic 5D-"observations" are recursively defined by
where
The filters
and offsets m(^) are preset values,
s = s(t) represents the state of the model, with
The event data is generated with a similar model. We use five states with the same transition probabilities. To simulate events, we changed the offsets m(s) (Set 1), we used noisy filters
respectively, and we used Gaussian noise only (Set 4). We generated each 50000 normal case and event observations.
3.1.b Tested models. We build a LPM with
predictors. We use p = 10 previous observations to predict the following one, and in the training, we use 15 observations to estimate one predictor (n = 14, see Section 2.1). For the GMM, we tried several numbers of Gaussians from five to one hundred. We decided to use ten Gaussians for the comparison, because with this, we have obtained the best results in our tests. The HMM consists of ten states. Each state is associated with a Gaussian distribution [7] (Gaussian Hidden Markov Model, GHMM).
Fig. 1. ROCs of (a) the LPM, (b) the GMM, (c) the GHMM and (d) overview of (a), (b) and (c), computed using all test sets at once
3.1.c Results. In Figure 1, we can see different Receiver Operating Characteristics (ROCs) of the three models. The ROC is the curve that results if we plot the probability to correctly detect an event (p(TP)) against the probability that an normal observation is falsely classified as an event (p{FP)), that is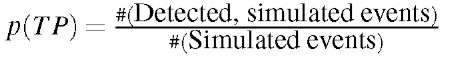
and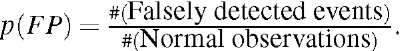
A method is superior to another one at a fixed false positive rate if its ROC curve is above another ROC. In order to reduce false alerts and respect that events are rare occurrences, we are particularly interested in parameters with low false positive rates.
In Figure 1(a), 1(b) and 1(c), we can see the performance of the different models separately, one ROC for each test. In Figure 1(d), we can see the overall performance (results using all event datasets as one set) of each model.
Comparing the GHMM and the GMM, the GHMM performs better. But as we can see in Figure 1(a) and 1(d), the LPM outperforms both methods. Hence, there are event detection problems where the LPM can be successfully applied, and they perform better than GMMs or GHMMs. In the next section, we apply the LPM on real data.
Car Tracking and Event Detection
The setup of this test is as follows. A web cam is positioned to monitor a fixed area. We drive an RC car in the visible area and perform several actions. The "normal case" consists of any combination of normal movements (driving straight, turning left or right), an "event" is an arbitrary action that differs from these possible actions (for example, if the car hits another object).
To adapt the LPM to tracking and motion detection, every time window of p observations is rotated so that the difference vector of the first two is orientated in one particular direction. This simplifies the prediction, and reduces the number of predictors.
3.2.d Tracking. We use a background subtraction algorithm [6] for the motion detection. This algorithm estimates for every image of a video sequence the foreground and updates a background model. It uses one threshold for each pixel. It is similar to many other background subtraction algorithms, but we have adapted it to our problem, especially to color images.
In detail, let
be the (normalized color) pixel
of the tth back ground image,
the corresponding pixel in the tth measured image,
the tth threshold for pixel
. We say,
belongs to the foreground
if
is fore
ground, and 0 otherwise, than
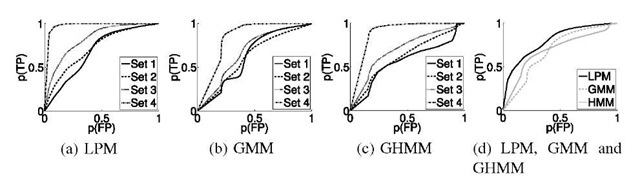
where
The constant 0.01 is used for noise suppression, aB e (0,1) controls the adaption to the background of C. The resulting blob (all foreground pixels) for several frames can be seen in Figures 3(a) and 3(b).
3.2.e Extended model. We model a special case of an AR model in this test (see Equation (1)),
and we assume p = 3. In this test, x(t) is the position of the car at frame t, one dimension of a0 represents the forward movement, the other one the drift. We use this adaption because we assume these two values to be very different. This adaption implies that
is used for the Yule-Walker equations instead of the X(t) assumed in Section 2.1. We use for Equation
. This scaling is used for visualization only.
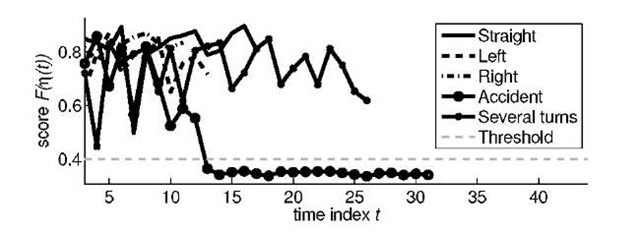
We use three predictors, one for straight parts, one for turning left and one for turning right. As weights, we set w(1) = w(2) = w(3) = 1/3. If the score F is lower than 0 = 0.4, we say, we have detected an event. In general, 0 is an arbitrary threshold with 
, and 0 = 0.4 is sufficient for our task, as we have verified with some test data (see Figure 4).
Fig. 2. Frames from the training data: the car turns left(a), drives straight (b) and turns right (c)
3.2.f Training data. The predictors are estimated only for the basic actions. That means, the predictor for straight movement is estimated using only a video where the car moves in one particular direction, and the turns are estimated using videos including only the turns, but no straight parts. A normal activity is any combination of these actions. For each action, less than hundred data vectors were sufficient; for many other models, we would have to use more features, depending on the complexity of the model.
Fig. 3. Several frames from an accident video and the blobs of the tracking (a), and normal activities: car is driving in an S-bend (b)
3.2.g Results. In Figure 3(a), we see several frames of a video we use, that is the first frame with an detected object, immediately before an accident, the frame that has been captured during the accident, the following one and at the last frame of the sequence. The mark on the upper left denotes an event. The event is detected right after the accident.
In Figure 3(b), we see the car, performing an S-bend. This action is correctly classified as normal activity, and no events are detected.
Fig. 4. Score F as described in Section 2.3
In Figure 4, we can see the score F of several normal movements and an accident (an event). As we can see, the score of the normal activities is above the threshold. The same is true for the event video until the accident happens, than the score drops below the threshold and keeps at this low level.
Conclusion and Outlook
We have described and tested a method for event detection based on a mixture of linear predictions. Our model outperforms a GMM and a GHMM in a set of tests, despite being less complex than the latter one.
In contrast to GMMs, the LPM uses time dependencies for an improved decision. Furthermore, the LPM is a descriptive model, while the GMM and the GHMM are generative ones. However, LPMs and GMMs have the same simplicity in the inference. The estimation of the LPM is the easiest, because we do not need to estimate covariances, which can be difficult.
Further, we can adapt the LPM easily if the normal case changes by adding new predictors and calculate the weights on some new measurements. This adaption is not useful for GMMs, because it alters the probability of all observations, and HMMs have to be calculated from scratch.
Some problems with the LPM arise from the solution of the Yule Walker equations. For example, in the presence of outliers, the accuracy of the predictor estimation decreases, and if the variance in the data is too low, the number of values to estimate a linear predictor increases. Solutions to these problems are available within the frame of the Yule Walker equations. Because the LPM builds upon these equations, these solutions are available for the LPMs as well.
