Abstract
Maximum a posteriori (MAP) in the scope of the Bayesian framework is a common criterion used in a large number of estimation and decision problems. In image reconstruction problems, typically, the image to be estimated is modeled as a Markov Random Fields (MRF) described by a Gibbs distribution. In this case, the Gibbs energy depends on a multiplicative coefficient, called hyperparameter, that is usually manually tuned [14] in a trial and error basis.
In this paper we propose an automatic hyperparameter estimation method designed in the scope of functional Magnetic Resonance Imaging (fMRI) to identify activated brain areas based on Blood Oxygen Level Dependent (BOLD) signal.
This problem is formulated as classical binary detection problem in a Bayesian framework where the estimation and inference steps are joined together. The prior terms, incorporating the a priori physiological knowledge about the Hemodynamic Response Function (HRF), drift and spatial correlation across the brain (using edge preserving priors), are automatically tuned with the new proposed method.
Results on real and synthetic data are presented and compared against the conventional General Linear Model (GLM) approach.
Keywords: HyperParameter, Estimation, Bayesian, fMRI, HRF.
Introduction
The detection of neuronal activation based on BOLD signals measured using fMRI is one of the most popular brain mapping techniques.
The data are classically analyzed using the Statistical Parametric Mapping (SPM) technique [11,10] where the General Linear Model GLM is used to describe the observations at each voxel and the corresponding coefficients are estimated by using the Least Square Method [14]. The detection of the activated regions is performed from the estimated explanatory variables (EV’s) by using a second step of classical inference approach based on the Neyman-Pearson theorem.
Still, Bayesian approaches have been gaining popularity since they provide a formal method of incorporating prior knowledge in data analysis [6,12]. In [8], Groutte et al. propose a non-parametric approach where a Finite Impulse Response (FIR) filter is used to describe the HRF and smoothing constraints are imposed at the solution by using a regularization matrix. Ciuciu et al. describe another non-parametric approach for the Bayesian estimation of the HRF in [3]. The authors make use of temporal prior terms to introduce physiological knowledge about the HRF. Basic and soft constraints are incorporated in the analysis, namely the considerations that the HRF starts and ends at zero and that the HRF is a smooth function. In [16] the authors propose a Bayesian approach in which the data noise is estimated using a spatio-temporal model and propose a half-cosine functions HRF model based on their experimental findings. In Yet another Bayesian approach based on the mathematical formalism of the GLM is proposed in [1]. The authors describe an SPM algorithm based on the maximum a posteriori (MAP) criterion to jointly estimate and detect the activated brain areas characterized by binary coefficients. The prior term introduced for these parameters comprises a bimodal distribution defined as the sum of two Gaussian distributions centered at zero and one.
In this paper we further improve this last method [1] by implementing an automatic HyperParameter estimation method to automatically set the prior strength in the Bayesian estimation of a MRF described by a Gibbs distribution. Additionally, data drift estimation is incorporated and the spatial correlation between neighbors is taken into account by using edge preserving priors that promote piecewise constant region solutions. The optimization of the overall energy function with respect to the activation binary variables is performed by using the graph-cuts (GC) based algorithm described in [2], which is computationally efficient and is able to find out the global minimum of the energy function.
Problem Formulation and Method
By making use of the problem formulation and variables defined in [1] we further incorporate a slow time data drift variable (a.k.a. baseline) di of time dimension N into the observation model, yielding eq. 1 at each ith voxel, when L stimuli are applied simultaneously.
where yi(n) is the N length observed BOLD signal at the ith voxel, hi(m) is the![]() dimensional HRF and n(n) is noise signal. The activity unknowns
dimensional HRF and n(n) is noise signal. The activity unknowns![]() are binary with
are binary with![]() voxel is activated by the
voxel is activated by the
![]() is assumed Additive White Gaussian Noise (AWGN) which is an acceptable assumption mainly if a prewhitening preprocessing [9] of the data is performed.
is assumed Additive White Gaussian Noise (AWGN) which is an acceptable assumption mainly if a prewhitening preprocessing [9] of the data is performed.
The maximum a posteriori (MAP) estimation of the unknown column vectors
![]() is obtained, in matrix form, by minimizing the following energy function
is obtained, in matrix form, by minimizing the following energy function
where the prior terms incorporate the a priori knowledge [13] about the temporal behavior of hj and dj – the HRF (C1) starts and ends at 0; (C2) is smooth; (C3) has similar magnitude to the HRF one gamma function (hc(t)) proposed in [5,9]; and that the dj is (C4) a slow varying signal with a smaller bandwidth than the one of hj.
By the Hammersley-Clifford theorem [7] and Markov Random Fields theory, these constraints may be imposed in the form of the following Gibbs distributions
where Zh and Zd are partition functions and the Gibbs energies U(hj) and U(dj) are designed in the following way, where [a, y] are regularization parameters to tune the degree of smoothness of the estimated vectors.
Here the weigh coefficients![]() where the discrete version of the HRF gamma function is
where the discrete version of the HRF gamma function is![]() are used to compensate for the reduced prior strength when the second derivatives are small. Its can be shown that the overall energy eq. (2) is rewritten as follows
are used to compensate for the reduced prior strength when the second derivatives are small. Its can be shown that the overall energy eq. (2) is rewritten as follows
where Ho = diag{hd(n)} is a M x M diagonal matrix containing the HRF. Dh and Dd are M x M and N x N second and first order difference matrix operators [14], respectively.![]() is a toeplitz L x N convolution matrix of bj and bj as defined in [1]
is a toeplitz L x N convolution matrix of bj and bj as defined in [1]
Optimization
The MAP estimation of the unknown vectors bj, hj and dj is obtained by minimizing the energy function (7) with respect to each vector, one step at a time. bj is first estimated with the drift initialized with the mean of the![]() and h0 equal to hd(n) [5,9].
and h0 equal to hd(n) [5,9].
Step One: b Estimation
Its easily shown that the binary elements of![]() that leads to the minimization of (7) are a simple binarization by thresholding (thrs = 0) of the following fields, in matrix notation, where
that leads to the minimization of (7) are a simple binarization by thresholding (thrs = 0) of the following fields, in matrix notation, where![]()
To solve this huge combinatorial problem, a fast and computationally efficient graph-cuts based algorithm [2] is used to binarize the fields Btr l(k), defined in (8), at each (r,l) pixel location in the data slice, by minimizing the following energy function:
where![]() is the observed signal variance
is the observed signal variance![]() are XOR © operators between 3r,i (k) and its causal vertical
are XOR © operators between 3r,i (k) and its causal vertical![]() and horizontal
and horizontal![]() neighbors, respectively;
neighbors, respectively;![]() is the normalized (smoothed) filtered gradient of B(k). Non-uniform solutions to (9) have a higher cost due to the spatial regularization term. However, in order to preserve transitions, the division by grl reduces this non-uniform cost at locations where the gradient magnitude is large. It can be shown that (9) is convex which guaranties [2] global minimum convergence.
is the normalized (smoothed) filtered gradient of B(k). Non-uniform solutions to (9) have a higher cost due to the spatial regularization term. However, in order to preserve transitions, the division by grl reduces this non-uniform cost at locations where the gradient magnitude is large. It can be shown that (9) is convex which guaranties [2] global minimum convergence.
Step Two: h Estimation
A new estimation of hj is calculated by finding the null derivative point of (2) with respect to h, yelding:
where![]() is calculated with the current
is calculated with the current![]() vector, estimated at the previous iteration step 3.1. However, the HRF is only estimated in the case of voxel activation by at least one paradigm, i.e., if
vector, estimated at the previous iteration step 3.1. However, the HRF is only estimated in the case of voxel activation by at least one paradigm, i.e., if![]()
HyperParameter Estimation. In this method the regularization parameter a s not constant but is automatically and adaptively estimated along the iterative process as follows. Considering (5), we can rewrite eq. (3) as
where![]() is the 2nd derivative operator in (5). By assuming
is the 2nd derivative operator in (5). By assuming![]() to be a probability density function (of unitary area) and
to be a probability density function (of unitary area) and![]() we get
we get
hence the energy term of (2) with respect which implies that
hence the energy term of (2) with respect to h can be rewritten as
By finding the null derivative of (13) we obtain the automatic HyperParameter estimation that is, in each iteration, dependent on the initialization and current estimate of the HRF.
Step Three: d Estimation
A new estimation of di is calculated by finding the null derivative point of (2) with respect to di, yelding:
where I is the identity matrix and![]() is computed by using the current
is computed by using the current![]() vector, obtained in the previous iteration step.
vector, obtained in the previous iteration step.
Since y is a regularization parameter associated with the drift signal, a much slower frequency signal than HRF, then 7 should be higher than![]() [15]. Here 7 = 100a.
[15]. Here 7 = 100a.
Experimental Results
In this section tests with synthetic and real data are presented to illustrate the application of the algorithm and evaluate its performance.
Synthetic Data
The synthetic data is based on the well known Shepp-Logan image phantom with 256 x 256 pixels. The paradigm was generated in a block-design basis with 4 epochs, 60 sec each (30 sec of activation and 30 sec of rest) with TR = 3 sec.
Making use of (1) for generating the yi observed data, a Monte Carlo experiment with a total of 3, 276, 800 runs was performed with several different noise levels (see Fig. 1 captation). The resulting mean and standard deviation (error bars) values of probability of error (Pe), as a function of a, SNRdB and SNR, are presented in Fig.1. The results with and without GC are shown, as well as the ratio Pe(GC)/Pe(w/GC).
Fig.1. Monte Carlo results for 50 runs on 256 x 256 pixels, for a = {0.1, 0.25, 0.5, 0.75, 1, 1.5, 2, 2.5, 3, 4, 5}. The mean and standard deviation (error bars) values of Pe, as a function of a, SNRdB and SNR, are presented on the first, second and third columns, respectively. The results with and without GC are displayed on the top and middle rows, respectively, and the ratio [Pe(GC)/Pe(w/GC)] (a is displayed on the bottom row.
These results demonstrate the activity detection robustness of the method, even in highly noisy data. They also show that taking into account the spatial correlation among neighboring voxels leads to a significant decrease in Pe. As expected, the improvement increases when the amount of noise increases or, equivalently, the SNR decreases. This is observed by the monotonic increasing behavior of the [Pe(GC)/Pe(w/GC)] (a).
Real Data
The real data used in this paper was acquired in the scope of a previous study [4] were two volunteers with no history of psychiatric or neurological diseases participated in a visual stimulation and a motor task fMRI experiment. Functional images were obtained using echo-planar imaging (EPI) with TR/TE = 2000 ms/50 ms. Datasets were pre-processed and analyzed using the FSL software (http://www.fmrib.ox.ac.uk/fsl) for: motion correction; non-brain removal and mean-based intensity normalization. The data used in the standard SPM-GLM analysis using FSL (not for the proposed SPM-Drift-GC) was further pre-processed with spatial smoothing (Gaussian kernel, 5 mm FWHM) and high-pass temporal filtering (Gaussian-weighted least squares straight line fitting, 50 sec cut-off).
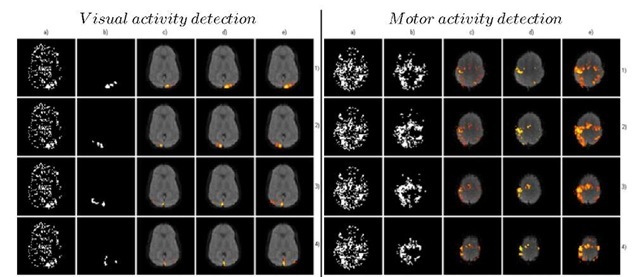
For the FSL processing a GLM approach with local autocorrelation correction was used on square stimulus functions convolved with the canonical Gamma HRF and it’s first derivative [5,9]. Linear stimulus/baseline contrast analysis and t-tests are applied to obtain the SPM, followed by cluster thresholding by the Gaussian Random Fields (GRF) theory. Since the results provided by this "’standard"’ method are depend on the inference p-value and clustering Z -score threshold values used, our experienced experimentalist provided two results of SPM-GLM: a relatively strict result and a more loose result, displayed on columns d) and e) of Fig. 2 respectively. The proposed SPM-Drift-GC method results are displayed on columns a), b) and c) of Fig. 2.
Fig. 2. Activated regions obtained by the new SPM-Drift-GC (a-b-c) and standard SPM-GLM (d-e) methods, on the visual (left) and motor (right) real data, where each row (1), 2), 3) and 4)) corresponds to a different stimulus. Left to right: a) Binary SPM-Drift algorithm results without GraphCuts; b) Binary SPM-Drift-GC algorithm results; c) Weighted SPM-Drift-GC algorithm results; d) SPM-GLM algorithm Strict results; e) SPM-GLM algorithm Loose results. Activation intensity is color coded from red (0) to yellow (1) and is overlaid on the EPI brain image with linearly decreasing transparency from 100% (activity = 0) to 0% (activity > 0.5).
In general, visual inspection of the activation brain maps suggests good agreement between the methods, although the SPM-Drift-GC also detects some regions not present in the strict results, but present, most of them, in the loose results. However, in some brain slices, there are areas only detected as active by SPM-Drift-GC that correspond to low energy estimated HRF’s (coded in transparent red) and somewhat deviant shaped HRF’s from the rigid HRF restrictions of SPM-GLM.
Conclusions
In this paper, a new data-dependent and automatic estimation method for the HyperParameters of a MRF described by a Gibbs distribution is proposed and applyed in the detection of activated brain areas in fMRI. Here, estimation and inference are joined together and the drift and HRF estimation and iteratively estimated by taking into account the spatial correlation.
Monte Carlo tests with synthetic data are presented to characterize the performance of the algorithm in terms of error probability. The introduction of the final step with graph-cuts greatly improves the accuracy of the algorithm, yielding an error probability that is close to zero even at the high noise levels observed in real data.
Real data activation results are consistent with a standard GLM approach, and most importantly, the activation clusters are best matched with the ones obtained at a significance threshold validated by the specialist, but with the advantage that the specification of user-defined subjective thresholds are not required. With the proposed method it also becomes unnecessary to apply spatial smoothing an high-pass temporal filtering as pre-processing steps, while accounting for important physiological properties of the data by estimating the HRF.








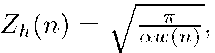


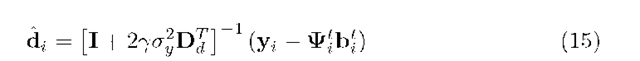
![Monte Carlo results for 50 runs on 256 x 256 pixels, for a = {0.1, 0.25, 0.5, 0.75, 1, 1.5, 2, 2.5, 3, 4, 5}. The mean and standard deviation (error bars) values of Pe, as a function of a, SNRdB and SNR, are presented on the first, second and third columns, respectively. The results with and without GC are displayed on the top and middle rows, respectively, and the ratio [Pe(GC)/Pe(w/GC)] (a is displayed on the bottom row. Monte Carlo results for 50 runs on 256 x 256 pixels, for a = {0.1, 0.25, 0.5, 0.75, 1, 1.5, 2, 2.5, 3, 4, 5}. The mean and standard deviation (error bars) values of Pe, as a function of a, SNRdB and SNR, are presented on the first, second and third columns, respectively. The results with and without GC are displayed on the top and middle rows, respectively, and the ratio [Pe(GC)/Pe(w/GC)] (a is displayed on the bottom row.](http://what-when-how.com/wp-content/uploads/2011/07/tmp368413_thumb.jpg)